Два тела с небольшой разницей в массах движущиеся по круговым орбитам вокруг общего центра масс. Этот специфический тип орбиты подобен системе Плутон - Харон. Постановка задачи

Пусть и радиус-векторы двух тел, а и их массы. Наша цель определить траектории и для любого времени t, при заданных начальных координатах и скоростях

, ,

, .

Второй закон Ньютона применительно к данной системе утверждает, что

где

— сила действующая на первое тело из-за взаимодействием со вторым телом, и

— сила действующая на второе тело со стороны первого.

Складывая и вычитая эти два уравнения, можно разделить одну задачу на две задачи с одним телом, которые могут быть решены независимо. "Сложение" уравнений (1) и (2) приводит к уравнению, описывающему движение центра масс . В отличие от этого, "вычитание" уравнения (2) из уравнения (1) приводит к уравнению, которое описывает, как вектор между массами изменяется со временем. Решение этих независимых задач может помочь в нахождении траекторий и .

Движение центра масс (первая задача)

Сложение уравнений (1) и (2) приводит к равенству

где мы использовали третий закон Ньютона и где

позиция центра масс системы. уравнение в итоге запишется в виде

Оно показывает, что скорость центра масс постоянна. Отсюда следует, что полный момент количества движения также сохраняется (сохранение импульса). Позиция и скорость центра масс может быть получена в любой момент времени.

Движения вектора смещения (вторая задача)

Вычитая уравнение (2) из уравнения (1) и преобразуя приходим к уравнению

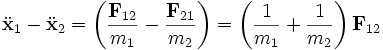
где мы снова использовали третий закон Ньютона и где (определённый выше) - вектор смещения, направленный от второго тела к первому.

Сила между двумя телами должна быть функцией только а не абсолютных положений и ; в противном случае задача не имеет трансляционной симметрии, то есть законы физики менялись бы от точки к точке. Таким образом можно записать:

где μ -приведённая масса

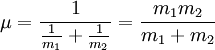
Как только мы найдём решение для и , первоначальные траектории можно записать в виде

как может быть показано подстановкой в уравнения для и .

Решение задачи двух тел

Согласно третьему закону Ньютона силы, с которыми тела действуют друг на друга, равны по величине и противоположны по направлению. Таким образом, для задачи двух тел можно записать

Проинтегрировав это уравнение два раза, получим

где a и b – некоторые векторы.

Обозначив через R и M координату центра тяжести двух тел и их суммарную массу соответственно

получим

то есть центр масс системы движется с постоянной скоростью.

Запишем силы, действующие на каждое из тел, следующим образом

    где    

Вычитая второе уравнение из первого, получим

    где    

Векторно умножая последнее уравнение на r и интегрируя, получим

Постоянный вектор h, являющийся постоянной интегрирования, называется кинетическим моментом системы. Взаимное движение тел происходит в плоскости, перпендикулярной этому вектору. Введём систему цилиндрических координат r, φ, z. Единичные векторы вдоль радиальной, трансверсальной и вертикальной оси обозначим как i, j и k. Проекции скорости на радиальную и трансверсальную оси составят

Тогда

В левой части последнего выражения стоит удвоенная площадь треугольника, описываемого радиус-вектором r за единицу времени. Таким образом, это соотношение является математической записью второго закона Кеплера.

Уравнение (1) умножаем скалярно на скорость и интегрируем. Получим

Подробный вывод

Распишем последнее выражение в координатах:

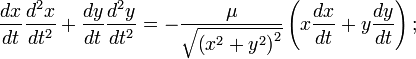
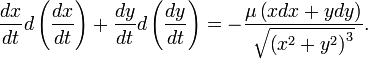
Заметим, что

Тогда

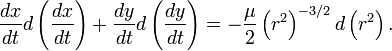
Интегрируя обе части, получим

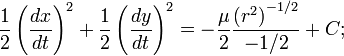
Последнее соотношение является выражением закона сохранения механической энергии в системе.