- •Основная задача динамики Основная задача динамики
- •Инерциальная систем координат связанная с Землёй
- •Единство понятия массы
- •Единицы массы
- •Закон сохранения
- •Равнодействующая
- •Понятие массы
- •«Школьное» определение импульса
- •Обобщённый импульс в аналитической механике
- •Формальное определение импульса
- •Импульс в квантовой механике Формальное определение
- •Определение через волны де Бройля
- •Заключение
- •Второй закон Ньютона
- •Другая формулировка Второго закона Ньютона . Импульс материальной точки
- •Третий закон Ньютона
- •Историческая формулировка
- •Кинематическая вязкость
- •Ньютоновские и неньютоновские жидкости
- •Вязкость аморфных материалов
- •Сила вязкого трения
- •Закон Гука
- •Нелинейные деформации
- •Пластические деформации
- •Обобщённый закон Гука
- •Законы Ньютона в неинерциальных системах отсчета
- •Состояние отсутствия веса (невесомость) наступает при удалении тела от притягивающего объекта, либо когда тело находится в свободном падении, то есть . Вес и масса
- •Интересные факты
- •Вес в авиации
- •Создание единой теории фундаментальных взаимодействий
- •Закон сохранения импульса. Центр инерции. Движение центра инерции. Связь закона сохранения импульса с принципом относительности Галилея
- •Принцип относительности Галилея и закон сохранения импульса
- •Обеспечивает передвижение ракетного двигателя и связанного с ним аппарата в сторону, противоположную направлению реактивной струи Формула при отсутствии внешних сил[2]
- •Доказательство
- •Уравнение Мещерского[2]
- •Формула Циолковского[3]
- •Момент импульса замкнутой системы сохраняется. Момент импульса в классической механике
- •Определение
- •Вычисление момента
- •Сохранение углового момента
- •Момент импульса в электродинамике
- •Момент импульса в квантовой механике Оператор момента
- •Симметрия вращения
- •Вычисление момента импульса
- •Предыстория
- •Единицы
- •Специальные случаи Формула момента рычага
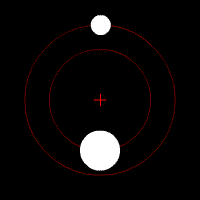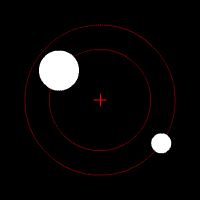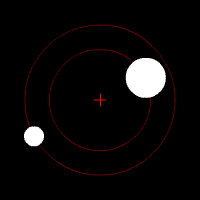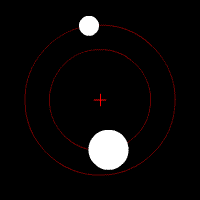
- •Два тела с небольшой разницей в массах движущиеся по круговым орбитам вокруг общего центра масс. Этот специфический тип орбиты подобен системе Плутон - Харон. Постановка задачи
- •Движение центра масс (первая задача)
- •Движения вектора смещения (вторая задача)
- •Решение задачи двух тел
- •Движение двух тел в плоскости
- •Общее решение для силы, зависящей от расстояния
- •Применение
- •Задача двух тел в ото
- •Первый закон Кеплера (закон эллипсов)
- •Второй закон Кеплера (закон площадей)
- •Третий закон Кеплера (гармонический закон)
- •Работа в термодинамике
- •Работа силы в теоретической механике
- •Определение
- •Размерность и единицы
- •Так как работа является мерой изменения энергии, мощность можно определить также как скорость изменения энергии системы. Единицы измерения
- •Мощность в механике
- •Электрическая мощность
- •Приборы для измерения мощности
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
![]() ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи Формула момента рычага
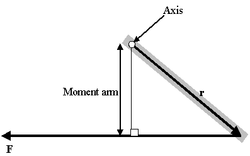
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
![]() =
МОМЕНТ РЫЧАГА * СИЛУ
=
МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
![]() =
РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
=
РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
![]() ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
![]() ,
,
То есть если I постоянная, то
![]() ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
![]() =
МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
=
МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
![]() =
МОМЕНТ СИЛЫ * УГОЛ
=
МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость
![]() в
радианах в секунду и время действия
МОМЕНТА
в
радианах в секунду и время действия
МОМЕНТА
![]() .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
= МОМЕНТ СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка
![]() ,
к которой приложена сила
,
то момент силы относительно точки
,
к которой приложена сила
,
то момент силы относительно точки
![]() равен
векторному произведению радиус-вектора
,
соединяющий точки O и OF,
на вектор силы
:
равен
векторному произведению радиус-вектора
,
соединяющий точки O и OF,
на вектор силы
:
![]() .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
В классической механике, задача двух тел состоит в том, чтобы определить движение двух точечных частиц, которые взаимодействуют только друг с другом. Распространённые примеры включают спутник, обращающийся вокруг планеты, планета, обращающаяся вокруг звезды, две звезды, обращающиеся вокруг друг друга (двойная звезда), и классический электрон, движущийся вокруг атомного ядра.
Задачу двух тел можно представить как две независимых задачи одного тела, которые привлекают решение для движения одной частицы во внешнем потенциале. Так как многие задачи с одним телом могут быть решены точно, соответствующая задача с двумя телами также может быть решена. В отличие от этого, задача с тремя телами (и, более широко, задача n тел) не может быть решена, кроме специальных случаев.
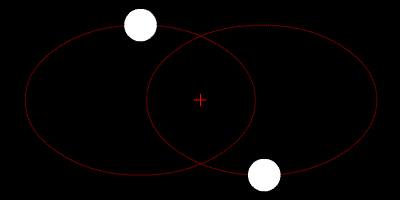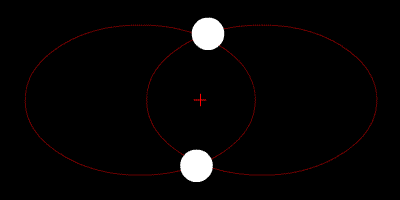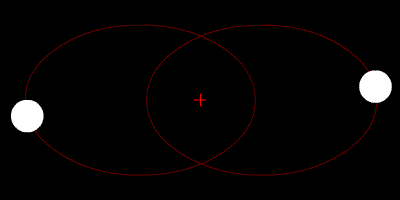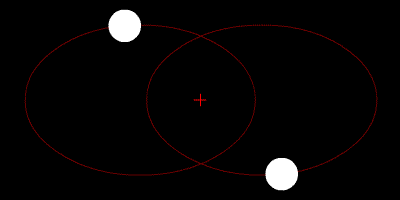
Два тела с одинаковой массой, движущиеся по кругу вокруг общего центра масс по эллиптическим орбитам.