Обеспечивает передвижение ракетного двигателя и связанного с ним аппарата в сторону, противоположную направлению реактивной струи Формула при отсутствии внешних сил[2]

Если нет внешних сил, то ракета вместе с выброшенным веществом является замкнутой системой. Импульс такой системы не может меняться во времени.

, где

- масса ракеты

- её ускорение

- скорость истечения газов

- расход массы топлива в единицу времени

Доказательство

До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю: , где

- изменение скорости ракеты

Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:

Произведение массы ракеты m на ускорение ее движения a по определению равно силе, вызывающей это ускорение:

Уравнение Мещерского[2]

Основная статья: Уравнение Мещерского

Если же на ракету, кроме реактивной силы , действует внешняя сила , то уравнение динамики движения примет вид:

Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами , действующими на тело, но и реактивной силой , обусловленной изменением массы движущегося тела:

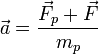
Формула Циолковского[3]

Основная статья: Формула Циолковского

Применив уравнение Мещерского к движению ракеты, на которую не действуют внешние силы, и проинтегрировав уравнение, получим формулу Циолковского:

Релятивистское обобщение этой формулы имеет вид:

, где – скорость света.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.

Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.

Момент импульса замкнутой системы сохраняется. Момент импульса в классической механике

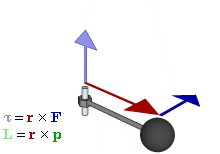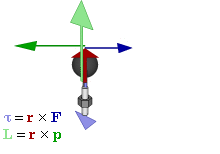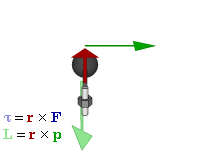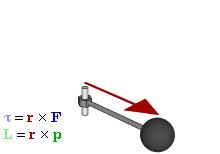
Связь между импульсом и моментом

Определение

Момент импульса частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:

где  — радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта,  — импульс частицы.

В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.

Из определения момента импульса следует его аддитивность. Так, для системы частиц выполняется выражение:

.

Вычисление момента

Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам и . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения. Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на нее можно указать ряд рецептов в соответствии с общими правилами нахождения векторного произведения двух векторов.

где  — угол между и , определяемый так, чтобы поворот от к производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения. Направление поворота важно при вычислении, так как определяет знак искомой проекции.

Запишем в виде , где  — составляющая радиус-вектора, параллельная вектору импульса, а  — аналогично, перпендикулярная ему. является, по сути, расстоянием от оси вращения до вектора , которое обычно называют «плечом». Аналогично можно разделить вектор импульса на две составляющие: параллельную радиус-вектору и перпендикулярную ему . Теперь, используя линейность векторного произведения, а также свойство, согласно которому произведение параллельных векторов равно нулю, можно получить еще два выражения для .

Для систем, совершающих вращение вокруг одной из осей симметрии (вообще говоря, вокруг так называемых главных осей инерции), справедливо соотношение

где  — момент инерции относительно оси вращения,  — вектор угловой скорости.

В общем случае вектор момента связан с вектором угловой скорости линейным оператором момента инерции: