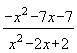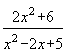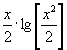2.4 Планы практических (семинарских) занятий

Практические занятия предназначены для получения и закрепления практических навыков решения различных задач математического обеспечения САПР. Все задания должны выполняться по указанию преподавателя в том порядке в котором они предлагаются студентам. Студенты пропустившие лекцию без уважительной причины не допускаются к практическим занятиям без отработки лекций.

Цель практических занятий – закрепить теоретический материал и дать студентам практические навыки по решению математических задач.

Практическое занятие №1. Решение задач с использованием прямых и итерационных методов решения систем линейных алгебраических уравнений.

Методические рекомендации: Внимательно изучите материал соответствующей лекции, выполните задания и ответьте на контрольные вопросы.

Задание 1. Решение системы линейных уравнений методом последовательного исключения неизвестных (методом Гаусса)

Цель: Получить навыки решения системы линейных уравнений методом последовательного исключения неизвестных (методом Гаусса)

Методические рекомендации. Разобрать решение примера 1 и решить примеры 2 и 3 по аналогии.

Пример 1. По схеме единственного деления решить систему

Решение. Запишем решение в таблицу

x1	x2	x3	x4	Свободные члены	∑1	∑2	Разделы схемы	 (невязка)
2	2	- 1	1	4	8		I
4	3	- 1	2	6	14
8	5	- 3	4	12	26
3	3	- 2	2	6	12
1	1	- 0,5	0,5	2	4	4
	- 1	1	0	- 2	- 2	- 2	II
	- 3	1	0	- 4	- 6	- 6
	0	- 0,5	0,5	0	0	0
	1	- 1	0	2	2	2
		- 2	0	2	0	0	III
		- 0,5	0,5	0	0	0
		1	0	- 1	0	0
			0,5	- 0,5	0	0	IV
			1	-1	0	0
			1	x4 = - 1	¯x4 = 0	0	V
		1		x2 = - 1	¯x2 = 0	0
	1			x3 = 1	¯x3 = 2	2
1				x1 = 1	¯x1 = 2	2

В раздел I таблицы вписываем матрицу системы, ее свободные члены и контрольные суммы. Затем подсчитываем «отмеченную» стро­ку этого раздела, разделив первую строку на а₁₁ = 2. Например, b₁₂=a₁₂/a₁₁= 2/2 = 1.

Элементы раздела II вычисляем по следующему правилу: каждый элемент этого раздела равен соответствующему элементу раздела I ми­нус произведение первого элемента его строки на элемент «отмеченной» строки в его столбце. Полученный результат записываем на соответст­вующее место в разделе II. Например:

Элементы «отмеченной» строки раздела II получим, разделив его пер­вую строку на ведущий коэффициент . Например,

Аналогично вычисляются элементы III и IV разделов. Например:

Для вычисления элементов раздела V, т. е. для нахождения неиз­вестных, используем «отмеченные» строки, начиная с последней.

Неизвестное x₄ представляет собой свободный член последней «от­меченной» строки: x₄ = = 1, а остальные неизвестные x₃, x₂ и x₁ получаются последовательно в результате вычитания из свободных членов «отмеченных» строк суммы произведений соответствующих ко­эффициентов на ранее найденные значения неизвестных.

Контроль осуществляется с помощью столбцов ∑₁ и ∑₂, Над столб­цом ∑₁ производятся те же действия, что и над остальными столбцами, и в итоге сумма элементов каждой строки схемы (без столбца ∑₁) должна быть равна элементу этой строки из столбца ∑₂. Числа из столбца ∑₁ должны быть равны числам 1 + х_j из столб­ца ∑₂.

В результате получаем x₁ = 1, x₂ = 1, х₃ = - 1, x₄ = - 1.

Пример 2. По схеме единственного деления решить следующую систему с точностью до 0,0001:

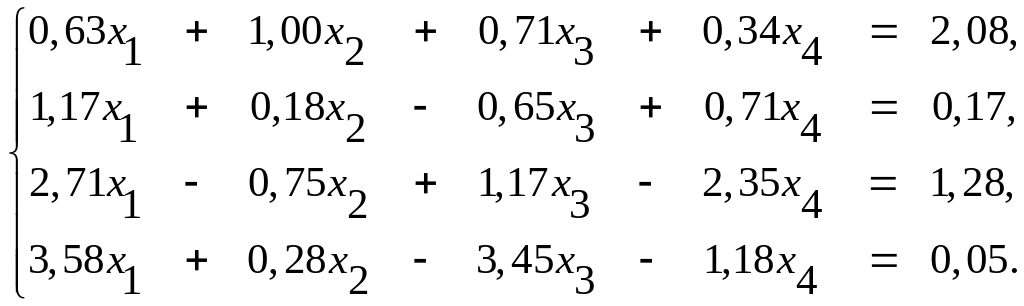
Пример 3. Решить методом Гаусса с тремя десятичными знаками систему

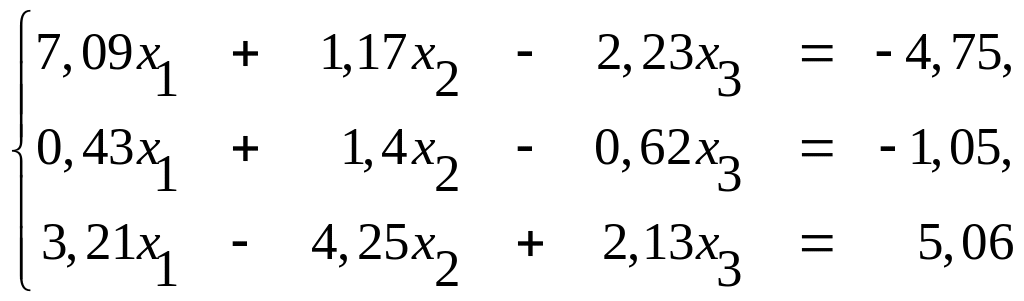
и уточнить полученные приближенные значения неизвестных до 10^-4.

Задание 2. Метод итерации и метод Зейделя.

Цель. Получить навыки решения системы линейных уравнений методом итерации

Методические рекомендации. Разобрать решение примера 1 и 2, решите самостоятельно пример3.

Пример 1. Решить систему методом итерации

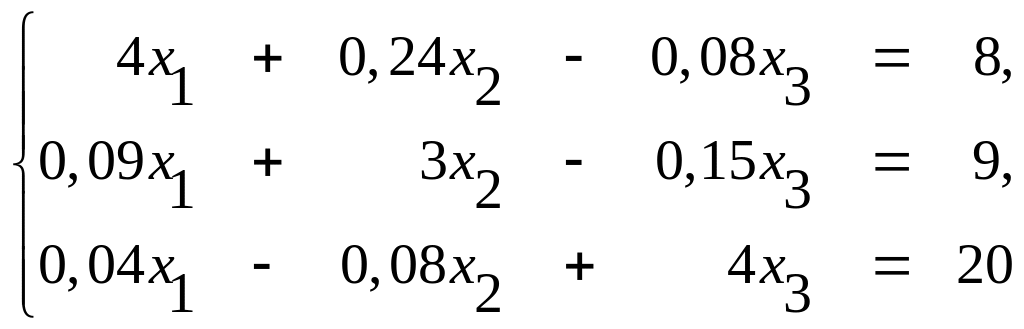
Решение. Диагональные коэффициенты преобладают значительно преобладают над остальными коэффициентами при неизвестных. Приведем эту систему к нормальному виду

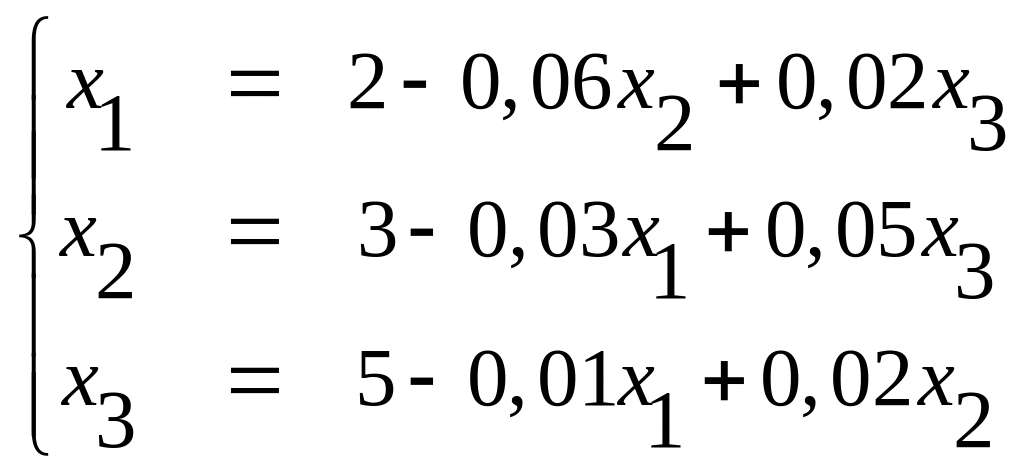
За нулевые приближения корней системы примем

Подставляя эти значения в правую часть системы уравнений, получим Далее, подставляя эти значения в правую часть системы уравнений, получим второе приближение

Повторяя подстановку получим новое приближение и т.д.

Пример 2. Решить систему методом Зейделя

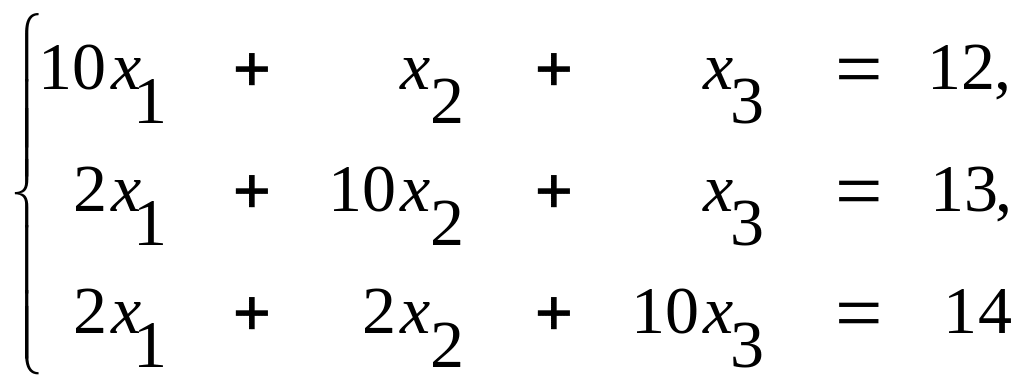
Решение. Приведем эту систему к удобному для итерации виду

В качестве нулевых приближений корней возьмем

Применяя процесс Зейделя, последовательно получим

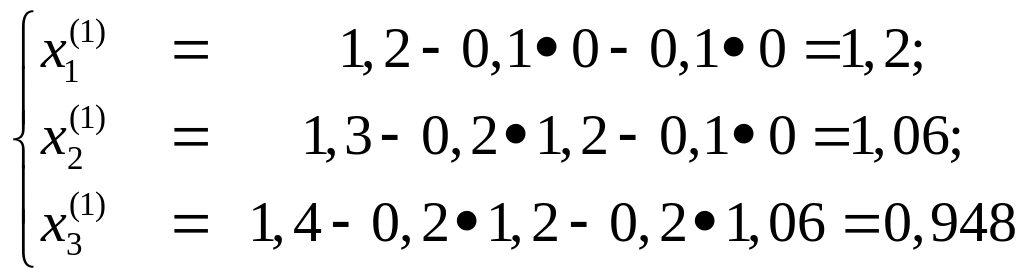
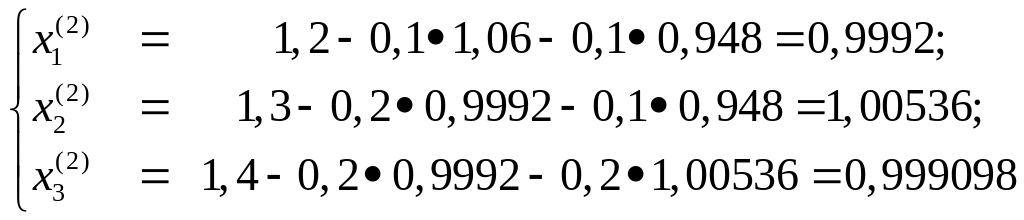и т.д.

На пятом шаге получим Для проверки точные значения корней

Пример 3. Решить систему методом итерации и методом Зейделя

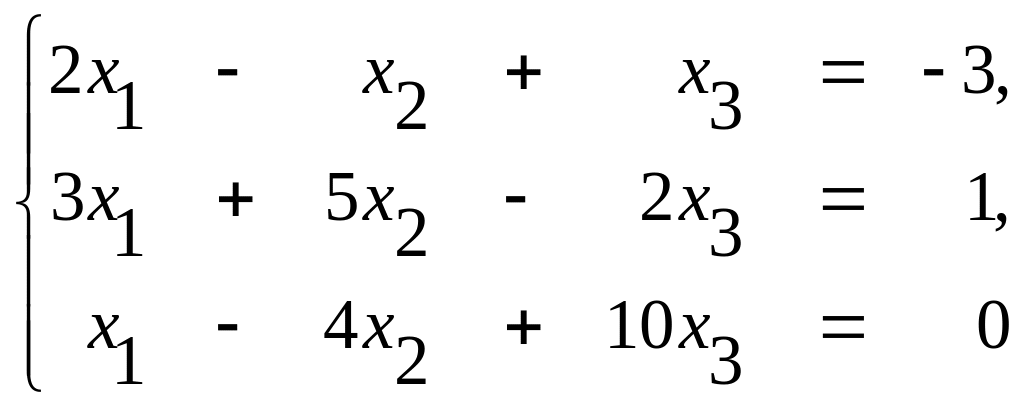
Рекомендуемая литература: о2[268-304], д1[32-34]

Контрольные вопросы:

1. Объясните метод Гаусса.

2. Объясните метод итерации.

3. Объясните метод Зейделя и чем он отличается от метода итерации.

Практическое занятие №2. Решение нелинейных и систем нелинейных уравнений с использованием численных методов. Вычисление корня уравнения с заданной точностью.

Методические рекомендации: Внимательно изучите материал соответствующей лекции, выполните задания и ответьте на контрольные вопросы.

Задание 1. Методом касательных решить примеры.

Пример 1. Методом касательных уточнить до ε = 0,001 корень уравнения х³ + Зх² — 3 = 0, расположенный на отрезке [—2,75; —2.5J.

Решение. f(—2,75) ∙ f″(х) > 0 Поэтому, чтобы воспользоваться методом касательных, сле­дует; выбрать х₀ = —2,75. Вычисления будем вести по формуле . Находим f'(х) = 3х² + 6х; f'(х₀) = f'(-2,75) = 6,1875.

Для удобства сведем все вычисления в таблицу, из которой видно, что |x₅ — x₄| < 0,001; поэтому ξ = 2,533.

n	xn	f(xn)
0	—2,75	—1,111	0,179
1	—2,571	—0,164	0,026
2	—2,545	—0,053	0,008
3	—2,537	0,020	0,003
4	—2,534	0,007	0,001
5	—2,533

Пример 2. Методом касательных уточнить до ε = 0,0001 корень уравнения х — sin х = 0,25, расположенный на отрезке [0,982; 1,178].

Задание 2. Методом хорд решить примеры.

Пример 1. Найти положительный корень с точностью до 0,002 уравнения

Решение. Отделим корень. Корень ξ лежит в интервале [1;2], т.к. интервал очень велик, поделим его пополам и получим интервал . [1;1,5].

Убедимся что конец а неподвижен, поэтому за нулевое приближение примем х₀=1,5. Последовательно применяя формулу , получим: х₁ = 1,15 ,

х₂ = 1,190 , х3 = 1,198 . Так как и при х₃  х  1,5 имеем 31,198² – 0,41,5 – 0,2 =3,49, то можно принять

Таким образом, ξ = 1,198 + 0,002, где 0   1. Для проверки точный корень уравнения ξ = 1,2.

Пример 2. Методом хорд уточнить до ε = 0,0001 корень уравнения х — sin х = 0,25, расположенный на отрезке [0,982; 1,178].

Рекомендуемая литература: о2[112-131], д1 [65-68], д1 [74-79]

Контрольные вопросы:

1. В чем заключается метод касательных?

2. В чем заключается метод хорд?

Практическое занятие №3. Решение задач с использование интерполяционных формул Лагранжа и Ньютона.

Цель: Получить навыки решения задач с использование интерполяционных формул Лагранжа и Ньютона.

Методические рекомендации. Изучить материал соответствующей лекции. Разобрать решение примера 1 и 2, решить примеры 3 и 4 по аналогии. Ответить на контрольные вопросы.

Пример 1. Для функции y = sin x построить интерполяционный полином Лагранжа, выбрав узлы y0 = 0, y1 = sin /6 = 1/2, y2 = sin /2 = 1.

Применяя формулу Лагранжа, получим

или .

Пример 2. Приняв шаг h=0,05 , построить на отрезке [3,5; 3,6] интерполяционный полином Ньютона для функции , заданной таблицей

x	3,50	3,55	3,60	3,65	3,70
y	33,115	34,813	36,598	38,475	40,447

Решение. Составим таблицу разностей. Так как разности третьего порядка практически постоянны, то полагаем n=3 . Приняв х₀=3,50, y₀=33,115, будем иметь:

x	y	 y	2 y	3 y	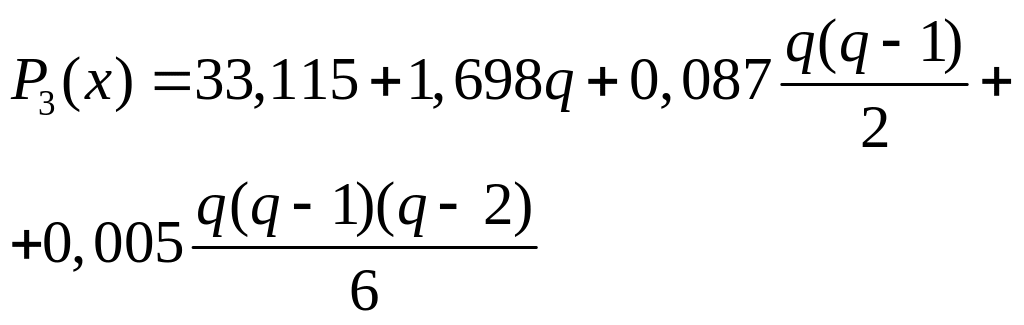, где
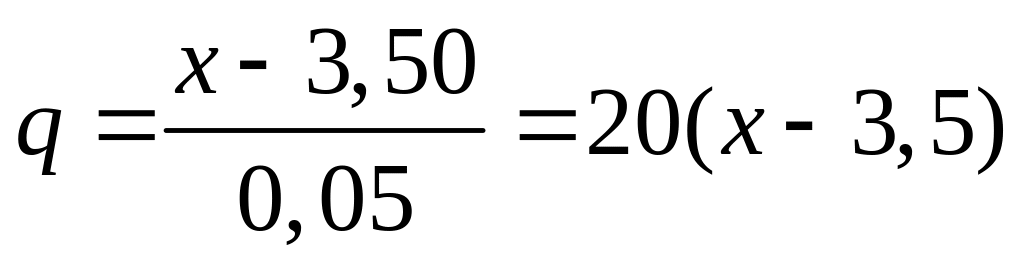
3,50	33,115	1698	87	5
3,55	34,813	1785	92	3
3,60	36,598	1877	95
3,65	38,475	1972
3,70	40,447

Пример 3. Дана таблица значений функции y=f(x). Вычислить значение f(323,5)

x	321,0	322,8	324,2	325,0
y	2,50651	2,50893	2,51081	2,51188

Пример 4. Дана таблица значений функции y=f(x). Вычислить значение f(0,45)

x	0,05	0,15	0,20	0,25	0,35	0,40	0,50	0,55
y	0,9512	0,8607	0,8187	0,7788	0,7047	0,6703	0,6065	0,5769

Примеры: Построить интерполяционный многочлен Лагранжа для равноотстающих узлов n=4

Варианты индивидуальных заданий.

Номер варианта		a	b	Номер варианта		a	b
1		-2	2	7		-2	3
2		-3	3	8		0	4
3		2	5	9		-3	3
4		-3	3	10		-3	3
5		-1	4	11		0	4
6		0	5	12		-2	3

Рекомендуемая литература: о2[497-561], 1д[109-111], 1д[113-117], 1д[120-122]

Контрольные вопросы:

1. Объясните как строится интерполяционный многочлен Лагранжа.

2. Интерполяционные формулы Ньютона. Когда они применяются?

3. Интерполяционные формулы Гаусса. Когда они применяются?

Практическое занятие №4. Решение задач численного интегрирования и численного дифференцирования.

Пример. Вычислить применяя формулу Ньютона-Котеса с семью ординатами (n=6).

Решение. h=1/6 , составим таблицу значений, где

i	xi	yi
0	0	1	41	41
1	1/6	6/7	216	185,142857
2	1/3	3/4	27	20,25
3	½	2/3	272	181,333333
4	2/3	3/5	27	16,2
5	5/6	6/11	216	117,818182
6	1	1/2	41	20,25
				581,994372

Отсюда y=581,994372 / 840 = 0,6933.

Задания численного интегрирования:

1. Вычислить значение определенного интеграла для различных значений n, по заданной квадратурной формуле (обобщенные формулы левых прямоугольников, правых прямоугольников, трапеций, парабол).

2. Вычислить значение определенного интеграла по одной из квадратурных формул Гаусса, Ньютона-Котеса при заданном значении n.

Проанализировать полученные результаты.

Варианты индивидуальных заданий.

Номер варианта		a	b	Номер варианта		a	b
1		-2	2	6		-3	0
2		-3	1	7		0	3
3		1	3	8		0	4
4		-2	1	9		0.1	2
5		2	4	10		1	4

Задание численного дифференцирования:

Найти функции , заданной таблично

x	y	y	2y	3y
50	1,6990	414	-36	5
55	1,7404	378	-31
60	1,7782	347
65	1,8129

Решение: Здесь h=5, тогда

Контрольные вопросы:

1. Формулы прямоугольников, трапеций для вычисления определенного интеграла.

2. Формула парабол для вычисления определенного интеграла.

3. Формула Ньютона-Котеса для вычисления определенного интеграла.

Рекомендуемая литература: о2[577-589], д1[127-139]

Практическое занятие №5. Решение обыкновенных дифференциальных уравнений численными методами.

Пример 1. Найти приближенное при х=1 значение решения уравнения удовлетворяющее начальному условию: .

Решение. Разделим отрезок [0; 1] на 10 частей, т.е. h=0,1, тогда применяя метод Эйлера получим

…

В процессе решения составляем таблицу

	1,000	1,000	0,100
	1,100	1,200	0,120
	1,220	1,420	0,142
	1,362	1,620	0,162
	1,524	1,924	0,1924
	1,7164	2,2164	0,2216
	1,9380	2,5380	0,2538
	2,1918	2,8918	0,2812
	2,4730	3,2730	0,3273
	2,8003	3,7003	0,3700
	3,1703

Мы нашли приближенное значение y|_x=1 = 3,1703.

Пример 2. Дано дифференциальное уравнение , удовлетворяющее начальным условиям y(0)=1,5. Вычислить с точностью до 0,01 решение этого уравнения при x=1,5. Вычисления проводить методом Рунге-Кутта с двумя запасными знаками.

Решение. Выбираем начальный шаг h вычислений из условия h⁴<0,01, тогда h<0,3. Для удобства возьмем h=0,25, весь отрезок [0; 1,5] при этом разобьется на шесть равных частей точками x₀=0, x₁=0,25, x₂=0,5, x₃=0,75, x₄=1,0, x₅=1,25 и x₆=1,50. Из начального условия x₀=0 и y₀=1,5. Найдем первое приближение y₁ +  y₀, где При этом коэффициенты =( y₀ - x₀) h=0,3750; 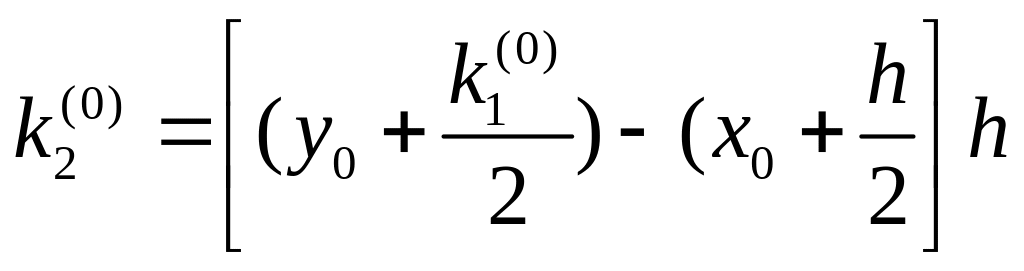=0,3906;

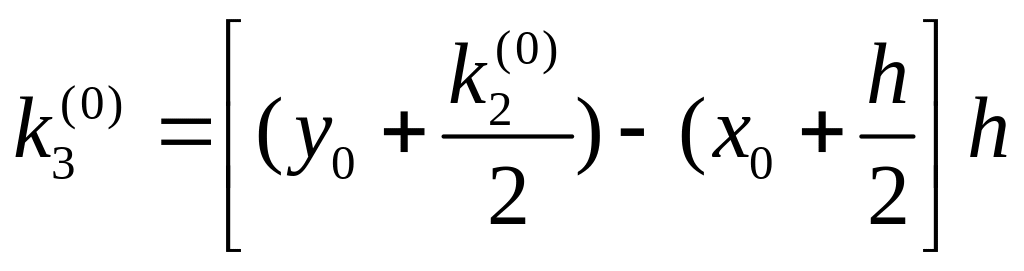=0,3926; =0,4106. Следовательно

=0,3920; y₁=1,5000+0,3920=1,8920.

И так далее в конечном итоге мы имеем y(1,5)=4,74.

Задания: Составить решение задачи Коши для обыкновенного дифференциального уравнения первого порядка методом Эйлера на отрезке [0,2; 1,2] с шагом =0,1 при начальном условии y(0,2)=0,25. Все вычисления выполнять с четырьмя десятичными знаками.

1. y′=0,133(x²+sin2x)+0,872y

2. y′=0,215(x²+cos1,5x) +1,283y

3. y′=0,158(x²+sin0,8x) +1,164y

4. y′=0,173(x²+cos0,7x) +0,754y

5. y′=0,221(x²+sin1,2x) +0,452y

6. y′=0,163(x²+cos0,4x) +0,635y

7. y′=0,218(x²+sin1,6x) +0,718y

8. y′=0,145(x²+cos0,5x) +0,842y

9. y′=0,213(x²+sin1,8x) +0,368y

10. y′=0,127(x²+cos0,6x) +0,573y

Контрольные вопросы:

1. Дайте постановки задачи Коши.

2. В чем заключается метод Эйлера?

Рекомендуемая литература: о3 [121-156], д1 [143-149]

Практическое занятие №6. Решение задач линейного программирования (Симплекс метод).

Пример. Для изготовления различных изделий А, В и С предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А, В и С, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в таблице 6.

Таблица 6

Вид сырья	Нормы затрат сырья (кг) на одно изделие			Общее количество сырья (кг)
	А	В	С
I	18	15	12	360
II	6	4	8	192
III	5	3	3	180
Цена одного изделия (тенге)	9	10	16

Изделия А, В и С могут производиться в любых соотношениях, но производство ограничено выделенным предприятию сырьем каждого вида.

Составить план производства изделий, при котором общая стоимость всей произведенной предприятием продукции является максимальной.

Решение. Составим математическую модель задачи. Искомый выпуск изделий А обозначим через х₁, изделий В — через x₂, изделий С — через x₃. Поскольку имеются ограничения на выделенный предприятию фонд сырья каждого вида, переменные х₁, x₂, x₃ должны удовлетворять следующей системе неравенств:

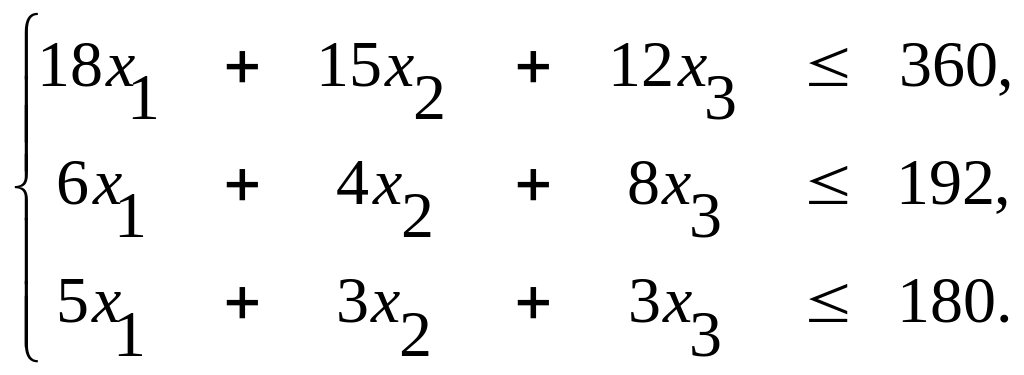(1)

Общая стоимость произведенной предприятием продукции при условии выпуска x₁ изделий А, х₂ изделий В и x₃ изделий С составляет

F = 9x₁ + 10х₂ + 16x₃ (2)

По своему экономическому содержанию переменные x₁, x₂ и x₃ могут принимать только лишь неотрицательные значения:

х₁, x₂, х₃>0. (3)

Таким образом, приходим к следующей математической задаче: среди всех неотрицательных решений системы неравенств (1) требуется найти такое, при котором функция (2) принимает максимальное значение.

Запишем эту задачу в форме основной задачи линейного программирования. Для этого перейдем от ограничений-неравенств к ограничениям-равенствам. Введем три дополнительные переменные, в результате чего ограничения запишутся в виде системы уравнений

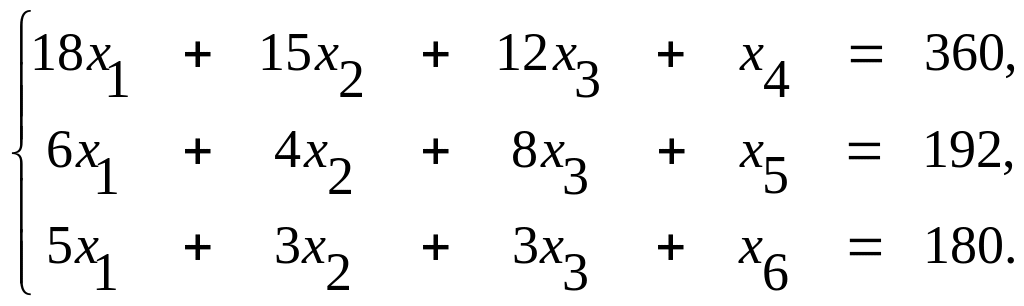
Эти дополнительные переменные по экономическому смыслу означают не используемое при данном плане производства количество сырья того или иного вида. Например, x₄ — это неиспользуемое количество сырья I вида.

Преобразованную систему уравнений запишем в векторной форме:

x₁P₁+x₂Р₂+x₃Р₃+x₄Р₄+x₅Р₅+x₆Р₆ = P₀,

где

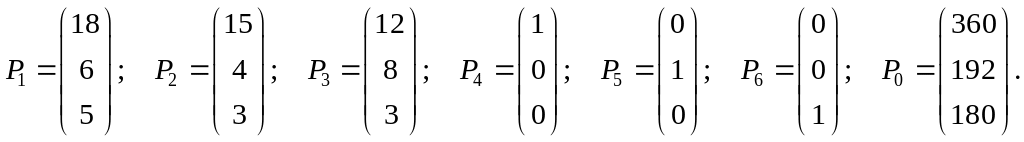
Поскольку среди векторов P₁, P₂, Р₃, Р₄, Р₅, Р₆ имеются три единичных вектора, для данной задачи можно непосредственно записать опорный план. Таковым является план X = (0; 0; 0; 360; 192; 180), определяемый системой трехмерных единичных векторов Р₄, Р₅, Р₆, которые образуют базис трехмерного векторного пространства.

Составляем симплексную таблицу для I итерации (таблица 7), подсчитываем значения F₀, z_j - с_j и проверяем исходный опорный план на оптимальность:

F₀ = (C, P₀) = 0, z₁=(С Р₁) = 0, z₂=(С, Р₂)=0; z₃=(С, Р₃) =0;

z₁ – с₁=0 - 9 = - 9, z₂ - с₂ = 0 - 10= -10, z₃ - с₃= - 16. Для векторов базиса z_j - с_j = 0.

Как видно из таблицы 7, значения всех основных переменных x₁, х₂, х₃ равны нулю, а дополнительные переменные принимают свои значения в соответствии с ограничениями задачи. Эти значения переменных отвечают такому «плану», при котором ничего не производится, сырье не используется и значение целевой функции равно нулю (т. е. стоимость произведенной продукции отсутствует). Этот план, конечно, не является оптимальным.

Таблица 7

i	Базис	C0	P0	9	10	16	0	0	0
				P1	P2	P3	P4	P5	P6
1	P4	0	360	18	15	12	1	0	0
2	Р5	0	192	6	4	8	0	1	0
3	Р6	0	180	5	3	3	0	0	1
4			0	-9	-10	-16	0	0	0

Это видно и из 4-й строки таблицы 7, так как в ней имеется три отрицательных числа: z₁ – c₁ = -9, z₂ - c₂= - 10 и z₃ – c₃ = -16. Отрицательные числа не только свидетельствуют о возможности увеличения общей стоимости производимой продукции, но и показывают, на сколько увеличится эта сумма при введении в план единицы того или другого вида продукции.

Так, число - 9 означает, что при включении в план производства одного изделия А обеспечивается увеличение выпуска продукции на 9 тенге. Если включить в план производства по одному изделию В и С, то общая стоимость изготовляемой продукции возрастет соответственно на 10 и 16 тенге. Поэтому с экономической точки зрения наиболее целесообразным является включение в план производства изделий С. Это же необходимо сделать и на основании формального признака симплексного метода, поскольку максимальное по абсолютной величине отрицательное число А, стоит в 4-й строке столбца вектора Р₃. Следовательно, в базис введем вектор Р₃. Определяем вектор, подлежащий исключению из базиса. Для этого находим θ₀ = min (b_i/а_i3) для а_i3>0, т. e. e_o = min (360/12; 192/8; 180/3) = 192/8.

Найдя число 192/8 = 24, мы тем самым с экономической точки зрения определили, какое количество изделий С предприятие может изготовлять с учетом норм расхода и имеющихся объемов сырья каждого вида. Так как сырья данного вида соответственно имеется 360, 192 и 180 кг, а на одно изделие С требуется затратить сырья каждого вида соответственно 12, 8 и 3 кг, то максимальное число изделий С, которое может быть изготовлено предприятием, равно min(360 / 12; 192 / 8; 180 / 3) = 192 / 8 = 24, т. е. ограни-чивающим фактором для производства изделий С является имеющийся объем сырья II вида. С учетом его наличия предприятие может изготовить 24 изделия С. При этом сырье II вида будет полностью использовано.

Следовательно, вектор Р₅ подлежит исключению из базиса. Столбец вектора Р₃ и 2-я строка являются направляющими. Составляем таблицу для II итерации (таблица 8).

Сначала заполняем строку вектора, вновь введенного в базис, т. е. строку, номер которой совпадает с номером направляющей строки. Здесь направляющей является 2-я строка. Элементы этой строки таблицы 8 получаются из соответствующих элементов таблицы 7 делением их на разрешающий элемент (т. е. на 8). При этом в столбце C_б записываем коэффициент С₃=16, стоящий в столбце вводимого в базис вектора Р₃. Затем заполняем элементы столбцов для векторов, входящих в новый базис. В этих столбцах на пересечении строк и столбцов одноименных векторов проставляем единицы, а все остальные элементы полагаем равными нулю.

Таблица 8

i	Базис	Cб	P0	9	10	16	0	0	0
				P1	P2	P3	P4	P5	P6
1	P4	0	72	9	9	0	1	- 3/2	0
2	Р3	16	24	3/4	1/2	1	0	1/8	0
3	Р6	0	108	11/4	3/2	0	0	-3/8	1
4			384	3	- 2	0	0	2	0

Для определения остальных элементов таблицы 8 применяем правило треугольника. Эти элементы могут быть вычислены и непосредственно по рекуррентным формулам.

Вычислим элементы таблицы 8, стоящие в столбце вектора Р₀. Первый из них находится в 1-й строке этого столбца. Для его вычисления находим три числа:

1. число, стоящее в таблице 7 на пересечении столбца вектора Р₀ и 1-й строки (360);

2. число, стоящее в таблице 7 на пересечении столбца вектора Р₃ и 1-й строки (12);

3. число, стоящее в таблице 8 на пересечении столбца вектора Р₀и 2-й строки (24).

Вычитая из первого числа произведение двух других, находим искомый элемент: 360—12-24 = 72; записываем его в 1-й строке столбца вектора Р₀ таблицы 8.

Второй элемент столбца вектора Р₀ таблицы 8 был уже вычислен ранее. Для вычисления третьего элемента столбца вектора Р₀ также находим три числа. Первое из них (180) находится на пересечении 3-й строки и столбца вектора Р₀ таблицы 7, второе (3) — на пересечении 3-й строки и столбца вектора Р₃ таблицы 7, третье (24) —на пересечении 2-й строки и столбца вектора Р₀ таблицы 9. Итак, указанный элемент есть 180 — 24-3=108. Число 108 записываем в 3-й строке столбца вектора Р₀ таблицы 8.

Значение Fo в 4-й строке столбца этого же вектора можно найти двумя способами:

1. по формуле F₀=(C, Р_о), т.е. F₀ = 0 – 72 + 16 – 24 + 0 – 108 = 384;

2. по правилу треугольника; в данном случае треугольник образован числами 0, -16, 24. Этот способ приводит к тому же результату: 0 - (-16) -24 = 384.

При определении по правилу треугольника элементов столбца вектора Р₀ третье число, стоящее в нижней вершине треугольника, все время оставалось неизменным и менялись лишь первые два числа. Учтем это при нахождении элементов столбца вектора Pi таблицы 8. Для вычисления указанных элементов первые два числа берем из столбцов векторов P₁ и Р₃ таблицы 7, а третье число — из таблицы 8. Это число стоит на пересечении 2-й строки и столбца вектора Р₁ последней таблицы. В результате получаем значения искомых элементов: 18 – 12 - (3/4) =9; 5 – 3 - (3/4) = 11/4.

Число z_i - c_i в 4-й строке столбца вектора P₁ таблицы 8 можно найти двумя способами:

1) по формуле z₁ – c₁ = (C, P₁) – c₁ имеем 0 – 9 + 16 - 3/4 + 0 - 11/4 - 9 = 3;

2) по правилу треугольника получим - 9 -(-16) - (3/4) = 3. Аналогично находим элементы столбца вектора Р₂. Элементы столбца вектора Р₅ вычисляем по правилу треугольника. Однако построенные для определения этих элементов треугольники выглядят иначе.

При вычислении элемента 1-й строки указанного столбца получается треугольник, образованный числами 0,12 и 1/8. Следовательно, искомый элемент равен 0 – 12 - (1 /8) = - 3/2. Элемент, стоящий в 3-й строке данного столбца, равен 0 – 3 - (1/8) = -3/8.

По окончании расчета всех элементов таблицы 8 в ней получены новый опорный план и коэффициенты разложения векторов Р ( ) через базисные векторы P₄, P₃, Р₆ и значения Δ'_j и F'₀. Как видно из этой таблицы, новым опорным планом задачи является план Х=(0; 0; 24; 72; 0; 108). При данном плане производства изготовляется 24 изделия С и остается неиспользованным 72 кг сырья I вида и 108 кг сырья III вида. Стоимость всей производимой при этом плане продукции равна 384 тенге. Указанные числа записаны в столбце вектора Р₀ таблицы 8. Как видно, данные этого столбца по-прежнему представляют собой параметры рассматриваемой задачи, хотя они претерпели значительные изменения. Изменились данные и других столбцов, а их экономическое содержание стало более сложным. Так, например, возьмем данные столбца вектора Р₂. Число 1/2 во 2-й строке этого столбца показывает, на сколько следует уменьшить изготовление изделий С, если запланировать выпуск одного изделия В. Числа 9 и 3/2 в 1-й и 3-й строках вектора Р₂ показывают соответственно, сколько потребуется сырья I и II вида при включении в план производства одного изделия В, а число — 2 в 4-й строке показывает, что если будет запланирован выпуск одного изделия В, то это обеспечит увеличение выпуска продукции в стоимостном выражении на 2 тенге. Иными словами, если включить в план производства продукции одно изделие В, то это потребует уменьшения выпуска изделия С на 1/2 ед. и потребует дополнительных затрат 9 кг сырья I вида и 3/2 кг сырья III вида, а общая стоимость изготовляемой продукции в соответствии с новым оптимальным планом возрастет на 2 тенге. Таким образом, числа 9 и 3/2 выступают как бы новыми «нормами» затрат сырья I и III вида на изготовление одного изделия В (как видно из таблицы 7, ранее они были равны 15 и 3), что объясняется уменьшением выпуска изделий С.

Такой же экономический смысл имеют и данные столбца вектора P₁ таблицы 8. Несколько иное экономическое содержание имеют числа, записанные в столбце вектора Р₅. Число 1/8 во 2-й строке этого столбца, показывает, что увеличение объемов сырья II вида на 1 кг позволило бы увеличить выпуск изделий С на 1/8 ед. Одновременно потребовалось бы дополнительно 3/2 кг сырья I вида и 3/8 кг сырья III вида. Увеличение выпуска изделий С на 1/8 ед. приведет к росту выпуска продукции на 2 тенге.

Из изложенного выше экономического содержания данных таблицы 8 следует, что найденный на II итерации план задачи не является оптимальным. Это видно и из 4-й строки таблицы 8, поскольку в столбце вектора Р₂ этой строки стоит отрицательное число —2. Значит, в базис следует ввести вектор Р₂, т. е. в новом плане следует предусмотреть выпуск изделий В. При определении возможного числа изготовления изделий В следует учитывать имеющееся количество сырья каждого вида, а именно: возможный выпуск изделий В определяется min (b’_i/а’_i2) для a’_i2 ≥ 0, т. е. находим

Следовательно, исключению из базиса подлежит вектор Р₄, иными словами, выпуск изделий В ограничен имеющимся в распоряжении предприятия сырьем I вида. С учетом имеющихся объемов этого сырья предприятию следует изготовить 8 изделий В. Число 9 является разрешающим элементом, а столбец вектора Р₂ и 1-я строка таблицы 8 являются направляющими. Составляем таблицу для III итерации (таблица 9).

Таблица 9

i	Базис	Cб	P0	9	10	16	0	0	0
				P1	P2	P3	P4	P5	P6
1	P4	10	8	1	1	0	1/9	-1/6	0
2	Р3	16	20	1/4	0	1	-1/18	5/24	0
3	Р6	0	96	5/4	0	0	-1/6	-1/8	1
4			400	5	0	0	2/9	5/3	0

В таблицы 9 сначала заполняем элементы 1-й строки, которая представляет собой строку вновь вводимого в базис вектора Р₂. Элементы этой строки получаем из элементов 1-й строки таблицы 8 делением последних на разрешающий элемент (т.е. на 9). При этом в столбце С_б данной строки записываем С₂ = 10.

Затем заполняем элементы столбцов векторов базиса и по правилу треугольника вычисляем элементы остальных столбцов. В результате в таблице 9 получаем новый опорный план Х=(0; 8; 20; 0; 0; 96) и коэффициенты разложения векторов P_j ( ) через базисные векторы Р₂, Р₃, Р₆ и соответствующие значения ∆"_j и F₀.

Проверяем, является ли данный опорный план оптимальным или нет. Для этого рассмотрим 4-ю строку таблицы 9. В этой строке среди чисел ∆"_j нет отрицательных. Это означает, что найденный опорный план является оптимальным и F_max = 400.

Следовательно, план выпуска продукции, включающий изготовление 8 изделий В и 20 изделий С, является оптимальным. При данном плане выпуска изделий полностью используется сырье I и II видов и остается неиспользованным 96 кг сырья III вида, а стоимость производимой продукции равна 400 тенге.

Оптимальным планом производства продукции не предусматривается изготовление изделий А. Введение в план выпуска продукции изделий вида А привело бы к уменьшению указанной общей стоимости. Это видно из 4-й строки столбца вектора P₁, где число 5 показывает, что при данном плане включение в него выпуска единицы изделия А приводит лишь к уменьшению общей величины стоимости на 5 тенге.

Решение данного примера симплексным методом можно было бы проводить, используя лишь одну таблицу в которой последовательно записаны одна за другой все три итерации вычислительного процесса.

Задания

1. Найти максимум функции F = 2x₁ — 6х₂ + 5х₅ при условиях

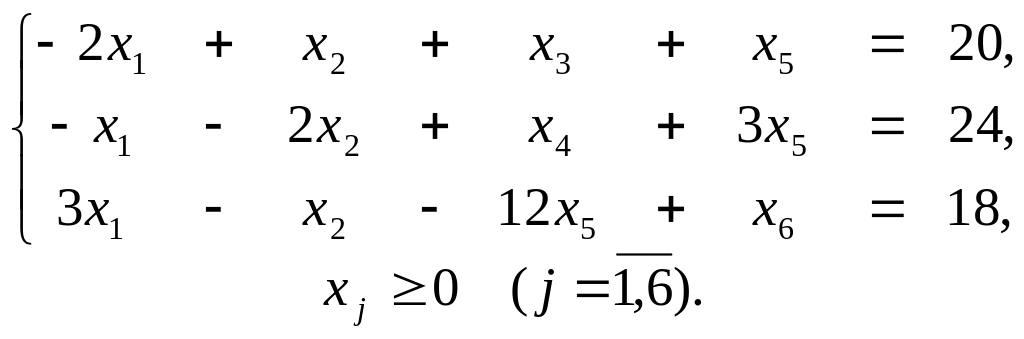
2. Найти решение задачи, состоящей в определении максимального значения функции F = 2х₁ + x₂ – х₃ + х₄ – x₅ при условиях

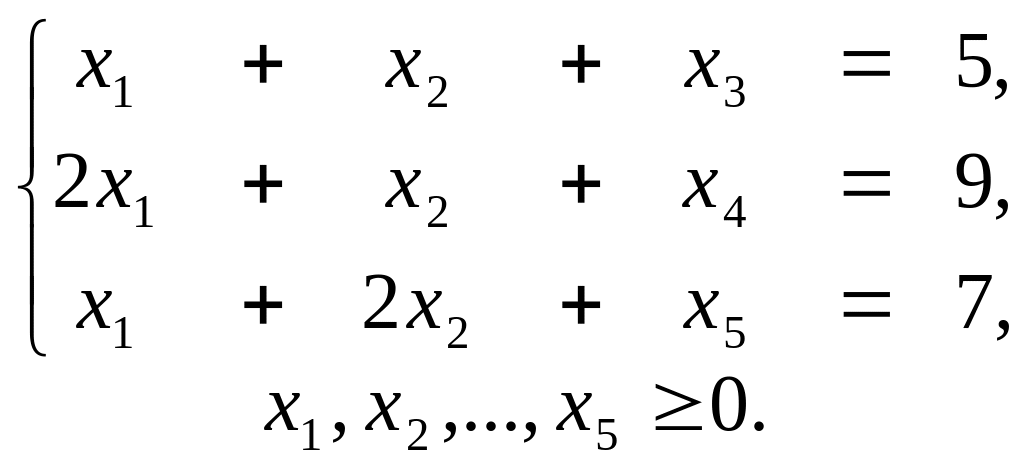
и дать геометрическую интерпретацию процесса решения.

3. Найти минимум функции F = - 2х₁ + Зx₂ - 6x₃ – x₄ при условиях

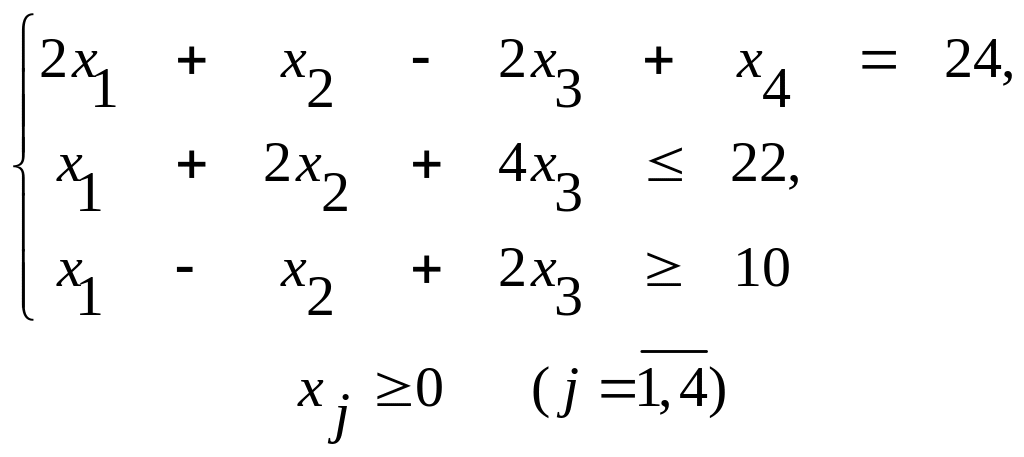
Контрольные вопросы:

1. Дайте математическую постановку задач линейного программирования.

2. В чем заключается Симплекс метод?

Рекомендуемая литература: о1[944-1000], о7[6-87]

Практическое занятие №7. Решение транспортных задач(метод северо-западного угла, мини­мального элемента, потенциалов).

Задача. На три базы А1 A2, A3 поступил однородный груз в ко­личествах, соответственно равных 140, 180 и 160 ед. Этот груз требуется перевезти в пять пунктов назначения В1, В2, В3, В4, B5 соответственно в количествах 60, 70, 120, 130 и 100 ед. Тарифы перевозок единицы груза с каждого из пунктов отправления в со­ответствующие пункты назначения указаны в следующей таб­лице:

Пункты отправления	Пункты назначения					Запасы
	В1	В2	B3	В4	В5
А1 A2 А3	2 8 9	3 4 7	4 1 3	2 4 7	4 1 2	140 180 160
Потребности	60	70	120	130	100	480

Найти план перевозок данной транспортной задачи методом северо-западного угла.

Решение. Здесь число пунктов отправления m = 3, а число пунктов назначения n = 5. Следовательно, опорный план задачи определяется числами, стоящими в 5 + 3 – 1 - 7 заполненных клетках.

Заполнение таблицы начнем с клетки для неизвестного х11, т. е. попытаемся удовлетворить потребности первого пункта назначе­ния за счет запасов первого пункта отправления. Так как запасы пункта А1 больше, чем потребности пункта B1, то полагаем x11 = 60, записываем это значение в соответствующей клетке табл. 2.3 и временно исключаем из рассмотрения столбец B1 считая при этом запасы пункта А1 равными 80.

Пункты отправления	Пункты назначения					Запасы
	В1	В2	B3	B4	В5
А1	2 60	3 70	4 10	2	4	140
А2	8	4	1 110	4 70	1	180
А3	9	7	3	7 60	2 100	160
Потреб­ности	60	70	120	130	100	480

Рассмотрим первые из оставшихся пунктов отправления А1 и назначения B2. Запасы пункта А1 больше потребностей пункта В2. Положим x12 = 70, запишем это значение в соответствующей клетке табл. 2.3 и временно исключим из рассмотрения стол­бец B2. В пункте A1 запасы считаем равными 10 ед. Снова рассмо­трим первые из оставшихся пунктов отправления А1 и назначе­ния В3. Потребности пункта В3 больше оставшихся запасов пункта A1. Положим x13=10 и исключим из рассмотрения стро­ку А1. Значение x13 =10 запишем в соответствующую клетку табл. 2.3 и считаем потребности пункта В3 равными 110 ед.

Теперь перейдем к заполнению клетки для неизвестного х23 и т. д. Через шесть шагов остается один пункт отправления A3 с запасом груза 100 ед. и один пункт назначения В5 с потреб­ностью 100 ед. Соответственно имеется одна свободная клетка, которую заполняем, полагая x35=100 (табл. 2.3). В резуль­тате получаем опорный план

Согласно данному плану перевозок, общая стоимость перево­зок всего груза составляет S=2*60 + 3*70 + 4*10+ 1*110+4*70 + 7*60 + 2*100=1380.

Метод минимального элемента.

Задача. Найти опорный план транспортной задачи предыдущего примера методом минимального элемента.

Решение. Исходные данные задачи запишем в виде таблицы. Минимальный тариф, равный 1, находится в клетке для переменной х13. Положим x13 = 160, запишем это значение в соот­ветствующую клетку таблицы и исключим временно из рассмо­трения строку A1. Потребности пункта назначения B3 считаем равными 30 ед.

В оставшейся части таблицы с двумя строками A2 и A3 и че­тырьмя столбцами B1, В2, B3 и В4 клетка с наименьшим значением тарифа cij находится на пересечении строки A3 и столбца B2, где c32 = 2. Положим х32 = 50 и внесем это значение в соответ­ствующую клетку табл. 2.4.

Временно исключим из рассмотрения столбец В2 и будем счи­тать запасы пункта А3 равными 120 ед. После этого рассмотрим оставшуюся часть таблицы с двумя строками А2 и A3 и тремя столбцами В1, B3 и В4. В ней минимальный тариф cij находится в клетке на пересечении строки А3 и столбца В3 и равен 3. Заполним описанным выше способом эту клетку и аналогично запол­ним (в определенной последовательности) клетки, находящиеся на пересечении строки A2 и столбца В1, строки A3 и столбца В4, строки A2 и столбца В4.

Пункты отправления	Пункты назначения				Запасы
	В1	B2	B3	В4
A1	7	8	1 160	2	160
A2	4 120	5	9	8 20	140
A3	9	2 50	3 30	6 90	170
Потребности	120	50	190	110	470

В результате получим опорный план

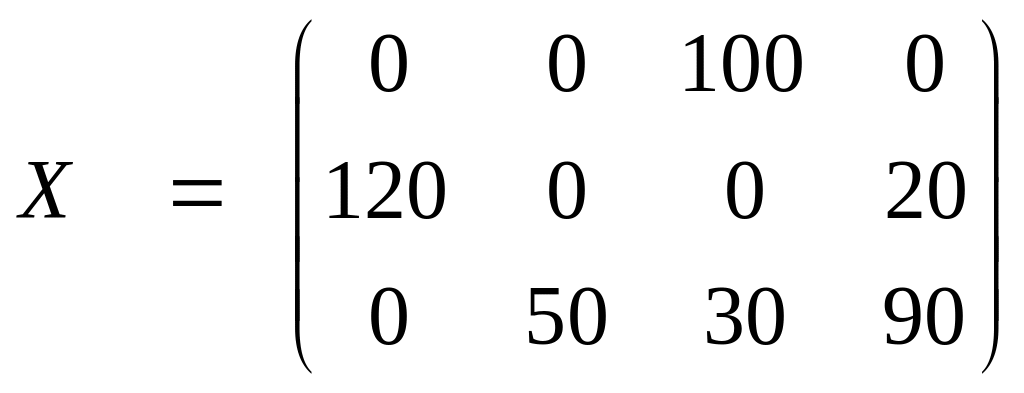
При данном плане перевозок общая стоимость перевозок со­ставляет

S=1*160 + 4*l20 + 8*20 + 2*50 + 3*30 + 6*90= 1530.

Задача.. Используя метод аппроксимации Фогеля, найти опор­ный план транспортной задачи, исходные данные которой приведены в таблице (опорный план этой задачи ранее был найден методом минимального элемента).

Пункты отправления	Пункты назначения				Запасы
	B1	В2	B3	В4
A1 А2 А3	7 4 9	8 5 2	1 9 3	2 8 6	160 140 170
Потребности	120	50	190	110	470

Решение. Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, запи­санными в данной строке или столбце, и поместим их в соответ­ствующем дополнительном столбце или дополнительной строке таблицы (см. ниже). Так, в строке А2 минимальный тариф равен 4, а следую­щий за ним равен 5, разность между ними 5 - 4=1. Точно так же разность между минимальными элементами в столбце В4 рав­на 6 - 2 = 4. Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу В4. В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки А1 и столбца В4. Таким образом, эту клетку следует заполнить. За­полнив ее, тем самым мы удовлетворим потребности пункта В4. Поэтому исключим из рассмотрения столбец В4 и будем считать запасы пункта А1 равными 160 - 110 = 50 ед. После этого опре­делим следующую клетку для заполнения. Снова найдем раз­ности между оставшимися двумя минимальными тарифами в каждой из строк и столбцов и запишем их во втором дополни­тельном столбце и во второй дополнительной строке таблицы. Как видно из этой таблицы, наибольшая указанная разность соответ­ствует строке А1. Минимальный тариф в этой строке записан в клетке, которая находится на пересечении ее с столбцом В3. Сле­довательно, заполняем эту клетку. Поместив в нее число 50, тем самым предполагаем, что запасы в пункте А1 полностью исчер­паны, а потребности в пункте B3 стали равными 190 - 50= 140 ед. Исключим из рассмотрения строку А1 и определим новую клетку для заполнения. Продолжая итерационный процесс, последова­тельно заполняем клетки, находящиеся на пересечении строки А3 и столбца В3, строки А3 и столбца B2, строки А2 и столбца В1,

Пункты отправления	Пункты назначения				За- па­сы	Разности по строкам
	B1	В2	B3	В4
А1	7	8	1	2	160	1	6	__	__	__	__
			50	110
А2	4	5	9	8	140	1	1	1	1	1	0
	120	20
А3	9	2	3	6	170	1	1	1	7	__	__
		30	140
Потребности	120	50	190	110	470
Разности по столбцам	3	3	2	4
	3	3	2	—
	5	3	—	—
	5	3	—	—
	—	0	—	—
	—	0	—	—

строки A₂ и столбца В₂. В результате получим опорный план

При этом плане общая стоимость перевозок такова:

S= 1*50 + 2*110 + 4*120 + 5*20 + 2*30 + 3*140= 1330.

Задания.

Методические рекомендации. Выполните задание применяя известные вам методы решения транспортных задач.

1. Найдите решение транспортной задачи, исходные данные кото­рой определяются таблицей

Пункты отправления	Пункты назначения				Запасы
	В1	В2	В3	В4
А1	5	4	3	4	160
А2	3	2	5	5	140
А3	1	6	3	2	60
Потребности	80	80	60	80