2 Содержание активного раздаточного материала

2.1 Тематический план курса составляется в виде таблицы, где указываются наименование темы и количество академических часов, предусмотренных для каждой темы.

Тематический план курса

№ п п	Наименование темы	Количество академических часов
		Лек ции	Лабо ратор ные	Практические	СРСП	СРС
1	Прямые и итерационные методы решения систем линейных алгебраических уравнений.	2	2	2	6	6
2	Численные методы решения нелинейных и систем нелинейных уравнений. Вычисление корня уравнения с заданной точностью.	2	2	2	6	6
3	Интерполяционные формулы Лагранжа. Конечные разности. Интерполяционные формулы Ньютона	2	2	2	6	6
4	Численное интегрирование и численное дифференцирование	2	2	2	6	6
5	Численные методы решения обыкновенных дифференциальных уравнений.	2	2	2	7	7
6	Линейное программирование. Симплекс метод. Решение двойственных задач.	3	3	3	7	7
7	Транспортная задача	2	2	2	7	7
		15	15	15	45	45

2.2 Конспект лекционных занятий Лекция №1 Прямые и итерационные методы решения систем линейных алгебраических уравнений.

Решением системы линейных уравнений (1) называется лю­бая совокупность чисел α₁, α₂, ..., α_n, которая, будучи подстав­ленной на место неизвестных x₁, x₂, ..., х_п в уравнения данной системы, обращает все эти уравнения в тождества.

Система линейных уравнений (1) называется совместной, если она имеет решение. Если система линейных уравнений не имеет решения, то она называется несовместной.

Совместная система линейных уравнений может иметь одно или несколько решений и называется определенной, если имеет одно единственное решение, и неопределенной, если имеет больше одного решения.

Для решения систем линейных уравнений существует множество методов, которые подразделяются на точные и приближенные. К точным методам относятся метод Крамера, метод главных элементов, метод Гаусса и другие. К приближенным относится метод итераций, метод релаксации и другие.

(1)

Решение системы линейных уравнений методом последовательного исключения неизвестных (методом Гаусса)

Наиболее распространенным методом решения систем ли­нейных уравнений является метод последовательного исключения неизвестных (метод Гаусса) являющийся частным случаем метода главных элементов..

Рассмотрим этот метод на примере системы четырех урав­нений с четырьмя неизвестными. Пусть дана система

(1)

Будем исключать неизвестное х₁ из всех уравнений системы (1), кроме первого. Назовем х₁ ведущим неизвестным, а коэф­фициент а₁₁ — ведущим коэффициентом. Разделив первое уравнение на а₁₁ , при условии что а₁₁ ≠ 0, получим

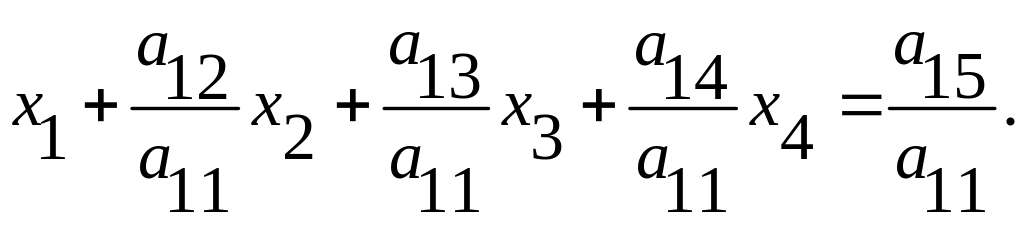
Обозначим а₁₂ /а₁₁ = b₁₂, а₁₃ /а₁₁ = b₁₃, а₁₄ /а₁₁= b₁₄, а₁₅ /а₁₁ = b₁₅ и вообще b_ij = а_1j /а₁₁ (j > 1). Тогда рассматриваемое уравнение примет вид

(2)

или

Для исключения неизвестного x₁ из уравнений системы (1) произведем следующие преобразования.

1) Из второго уравнения системы (1) вычтем уравнение (2), умноженное на a₂₁:

Обозначим

и перепишем полученное уравнение в виде .

2) Из третьего уравнения системы (1) вычтем уравнение (2), умноженное на а₃₁:

Обозначив и т. д., перепишем полученное уравнение в виде .

3) Из четвертого уравнения системы (1) вычтем уравнение (2), умноженное на а₄₁. Применив аналогичные обозначения, получим следующее уравнение:

.

В результате проведенных элементарных преобразований имеем систему трех уравнений с тремя неизвестными

(1´)

где коэффициенты a_ij (i,j ≥2) вычисляются по формуле ·

Разделив, далее, коэффициенты первого уравнения системы (1´) на ведущий коэффициент , получим первое урав­нение системы в виде

Обозначим ; ;

и вообще (j > 2). Тогда первое уравнение сис­темы (1´) примет вид

(2')

или

Исключая теперь x₂ из всех уравнений системы (1´), кроме первого, таким же способом, какими мы исключали x₁ придем к следующей системе из двух уравнений с двумя неизвестны­ми:

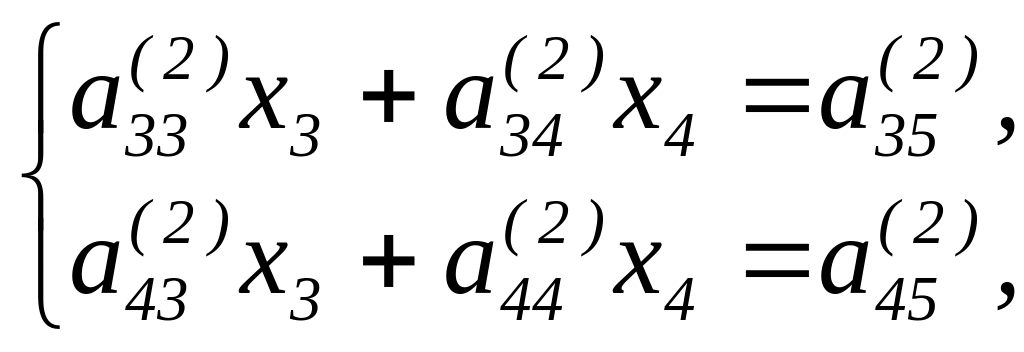(1″)

где (i, j ≥ 3). (Например, .) Разделив коэффициенты первого уравнения систе­мы (1") на ведущий коэффициент , получим

(2")

где (j > 3), т.e.

Исключив теперь x₃ аналогичным путем из системы (1"), находим

(1′″)

где (i, j ≥ 4). Отсюда

(2"')

Остальные неизвестные системы последовательно определяют­ся из уравнений (2"), (2') и (2):

Таким образом, процесс решения системы линейных урав­нений по методу Гаусса сводится к построению эквивалентной системы уравнений (2), (2'), (2"), (2"'). Метод Гаусса применим при том условии, что все ведущие коэффициенты отличны от нуля.

Для удобства вычисления производятся по схеме, называе­мой схемой единственного деления. Вычисле­ние элементов b_ij называется прямым кодом, вычисление зна­чений неизвестных — обратным кодом, так как сначала опре­деляется значение последнего неизвестного.

Схема единственного деления (схема Гаусса) составляется следующим образом.

В раздел I схемы записываются коэффици­енты при неизвестных (в столбцах соответствующих неизвест­ных), свободные члены и для каждой строки «контрольные сум­мы» (столбец ∑₂), равные сумме элементов а_ij в данной строке (здесь i = 1, 2, 3, 4; j = 1, 2, 3, 4, 5); последняя строка раздела I» состоящая из 1 и элементов b_ij, получается делением первой строки раздела на ведущий коэффициент a₁₁.

Элементы раздела II схемы равны соответствующим эле­ментам раздела 1 минус произведение а_i1b_1j (i,j ≥ 2); напри­мер, . Последняя строка раздела II, сос­тоящая из 1 и элементов , получается делением первой стро­ки раздела на ведущий коэффициент .

Аналогично вычисляются элементы III и IV разделов схе­мы. I, II, III и IV разделы, заканчивающиеся вычислением элементов (i = 1, 2, 3, 4; j = 2, 3, 4, 5) составляют пря­мой ход вычислений схемы.

Обратный ход начинается с вычисления последнего неизвестного системы линейных уравнений х₄ и заканчивается вычислением первого неизвестного х₁. При обратном ходе ис­пользуются лишь строки прямого хода, содержащие единицы и соответствующие элементы b_ij. (назовем эти строки «отмечен­ными»).

Элемент последней «отмеченной» строки и столбца сво­бодных членов дает значение x₄. Далее, остальные неизвест­ные x₃, x₂ и х₁ находятся вычитанием из свободного члена «от­меченной» строки суммы произведений ее коэффициентов на соответствующие значения ранее найденных неизвестных; на­пример, х₃ = .

Значения неизвестных последовательно выписываются в V раздел. Расставленные там единицы помогают находить для x_j соответствующие коэффициенты в «отмеченных» строках. Для контроля вычислений используются так называемые контрольные суммы:

(i = 1, 2, 3) и (i = 1, 2, 3, 4),

помещенные в столбце ∑₂.

В столбце ∑₁ разделов II, III и IV над контрольными суммами в каждой строке проделываются те же операции, что и над остальными элементами этой строки. При отсутствии ошибок в вычислениях элементы столбцов ∑₁ и ∑₂ равны. Таким образом, контролируется прямой ход схемы.

Для контроля обратного хода находится в последней «от­меченной» строке столбца ∑₁, т. е. , а остальные неиз­вестные этого столбца (j= 3, 2, 1) подсчитываются в тех же строках и по тем же формулам, что и неизвестные x_j , только в формулы подставляются соответствующие . В итоге числа должны совпадать с числами x_j + 1 из столбца ∑₂.

При большом числе неизвестных линейной системы схема Гаусса, дающая точное решение, становится сложной. В этих случаях удобнее пользоваться приближенными методами.

Метод итерации.

Пусть дана линейная система Ax=b. Предполагая, что диагональные коэффициенты a_ii≠0 (i = 1, 2, …, n), разрешим первое уравнение относительно x₁, второе относительно x₂ и т.д. Тогда получим эквивалентную систему

x = β + αx

приняв x⁽⁰⁾ = β, тогда x⁽¹⁾ = β + αx⁽⁰⁾, x⁽²⁾ = β + αx⁽¹⁾ и т.д. x^(k+1) = β + αx^(k) (k=1,1,2,…)

Полученную систему можно решить методом последовательных приближений или, как его называют, методом итераций.. В общем виде формулы приближений

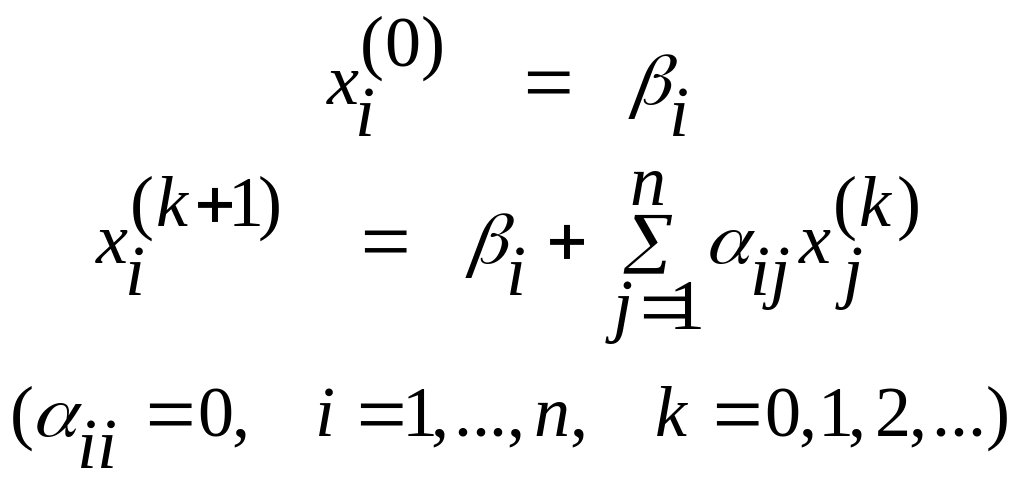
Сходящийся процесс обладает важным свойством самоисправляемости. Достаточное условие сходимости

или

Метод Зейлеля

Это модификация метода итерации Основная его идея заключается в том, что при вычислении (k+1)-го приближения неизвестной x_i учитываются уже вычисленные ранее (k+1)-е приближения неизвестных x₁, x₂, …, x_i-1.

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

(k=0, 1, 2, …)

Метод обеспечивает лучшую сходимость по сравнению с методом итерации.

Основная литература: 2[268-304], 1[126-138]

Контрольные вопросы:

1. Какими методами можно решить систему линейных алгебраических уравнений?

2. В чем заключается метод Гаусса?

3. В чем заключается метод итерации?

4. Чем отличается метод Зейделя от метода простой итерации?

Лекция №2 Численные методы решения нелинейных и систем нелинейных уравнений. Вычисление корня уравнения с заданной точностью.

Процесс нахождения приближенных значений корней уравнений разбивается на два этапа: отделение корней и уточнение корней до заданной степени точности.

Отделение корней.

Корень ξ уравнения f(x)=0 считается отделенным на отрезке [a,b] если на этом отрезке уравнение f(x)=0 не имеет других корней. Отделить корень – это значить разбить всю область допустимых значений на отрезки, в которых содержится один корень. Отделение можно производить двумя способами: графическим и аналитическим.

Для отделения корней графическим способом, необходимо построит график уравнения или , если это невозможно, то представить уравнение в виде (x)=(x) и построить графики функций y= (x) и y=(x). Абсциссы точек пересечения этих графиков и и будут искомые корни уравнения.

Порядок отделения корней аналитическим способом следующий:

1. находят f(x)

2. составить таблицу знаков функции f(x) полагая х равным:

а) критическим точкам или близким к ним;

б) граничным значениям.

3. определить интервал на концах которого функция принимает значения противоположных знаков.

Основываясь на общие свойства алгебраических уравнений можно перед тем как отделить корни определить число действительных корней уравнения. Для этого существует множество методов, один из них это теорема Штурма, которая дает наиболее точный результат. Теорема Штурма заключается в следующем:

Пусть дано алгебраическое уравнение P_n(x)=0 и для него каким либо способом установлено, что все действительные корни находятся в интервале (a,b) (причем a и b действительные числа и не являются корнями уравнения, a < b). Найдем первую производную P_n(x) и разделим на нее многочлен P_n(x). Остаток от деления возьмем с противоположным знаком и обозначим его через R₁(x). Затем P_n(x) делим на R₁(x), полученный остаток берем с противоположным знаком и обозначим через R₂(x). Потом R₁(x) делим на R₂(x) и остаток с противоположным знаком обозначим через R₃(x) и т.д. до тех пор пока остаток от деления не станет постоянной величиной. Эту величину так же берем с противоположным знаком. Получаем последовательность функций P_n(x), P_n(x), R₁(x), R₂(x), R₃(x), …, R_n=const, которая называется системой Штурма.

В эту последовательность вначале подставляем a , а затем b и подсчитываем числа перемен знака в обоих случаях, обозначим полученные числа через W(a) и W(b).

Теорема Штурма. Если действительные числа a и b не являются корнями многочлена P_n(x) не имеющего кратных корней, то W(a)  W(b) и равенство W(a) - W(b) равно числу действительных корней многочлена P_n(x), заключенным между a и b.

Теорема Штурма применяется также для отделения корней.

Отделив корни уравнения можно приступить к уточнению их любым из существующих методов.

Метод хорд.

Одним из распространенных методов решения алгебраических и трансцендентных урав­нений является метод хорд или его еще называют «метод ложного положения», «метод линейного интерполирования» и «метод пропорциональных частей».

Пусть дано уравнение f(х) = 0, где f(х) — непрерывная функция, имеющая в интервале (а, b) производные первого и второго порядков. Корень считается отделенным и нахо­дится на отрезке [а, b], т.е. f(а) · f(b) < 0.

Идея метода хорд состоит в том, что на достаточно малом промежутке (а, b) дуга кривой у = f(х) заменяется стягивающей ее хордой. В качестве приближенного значения корня принимается точка пересечения хорды с осью Ох.

При изучении вопроса об отделении корней мы рассмотрели различные варианты расположения дуги кривой в зависимости от знаков первой и второй произ­водных.

I случай: первая и вторая производные имеют одина­ковые знаки, т. е f'(х) · f″(х) > 0. Пусть, например, f(а) < 0, f(b) > 0, f'(х) > 0, f″(х) > 0 (рисунок 1, а). Гра­фик функции проходит через точки Α₀ (а; f(а)), В (b;f (b)). Искомый корень уравнения f(х) = 0 есть абсцисса точки пересечения графика функции у = f (х) с осью Ох. Эта точка нам неизвестна, но вместо нее возьмем, точку х_г пересечения хорды А₀В с осью Ох. Это и есть приближенное значение кор­ня.

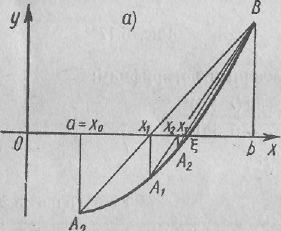
Рисунок 1

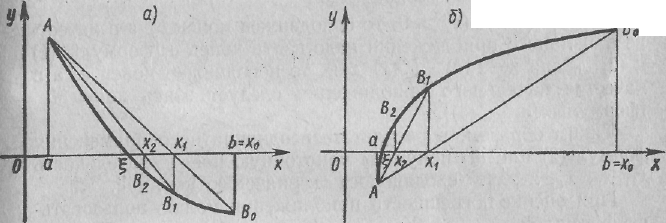
Рисунок 2

Уравнение хорды, проходящей через точки А₀ и В, имеет вид

Найдем значение х = x₁ для которого у= 0: (1)

Теперь корень ξ находится внутри отрезка [x₁, b]. Если зна­чение корня x₁ нас не устраивает, то его можно уточнить, при­меняя метод хорд к отрезку [x₁, b]. Соединим точку Α₁ (x₁; f(x₁)) с точкой В (b;f (b)) и найдем х₂ — точку пере­сечения хорды Α₁В с осью Ох:

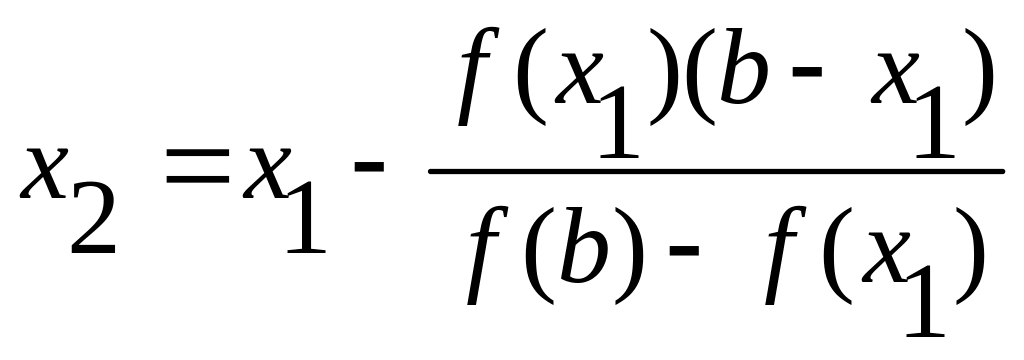и так далее, в общем виде (2)

Процесс продолжается до тех пор, пока мы не получим приближенный корень с заданной степенью точности. По приведенным выше формулам вычисляются корни и тогда, когда f(а) > 0, f(b) < 0, f'(х) < 0, f″(х) < 0 (рисунок 1, б).

ΙΙ случай: первая и вторая производные имеют раз­ные знаки, т. е.

f´(х) · f" (х) < 0. Пусть, например, f(а) > 0, f(b) < 0, f'(х) < 0, f″(х) > 0 (рисунок 2, а). Соединим точки А (а; f(а)) и В₀ (b; f (b)) и запишем уравнение хорды, про­ходящей через А и В₀:

Найдем x₁ как точку пересечения хорды с осью Ох, полагая у=0: (3)

Корень ξ теперь заключен внутри отрезка [a, х₁], применяя метод хорд к данному отрезку получим 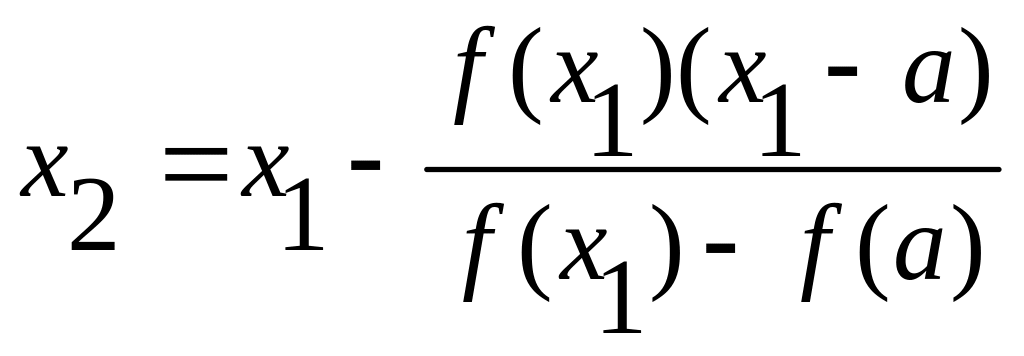и в общем виде (4)

По этим же формулам находится приближенное значение корня и тогда, когда f(а) < 0, f(b) > 0, f'(х) > 0, f″(х) < 0 (рисунок 2,б).

Итак, если f´(х) · f" (х) > 0, то приближенный корень вычисляется по формулам (1) и (2); если же f´(х) · f" (х) < 0, то по формулам (3) и (4).

Однако выбор тех или иных формул можно осуществить, пользуясь простым правилом: неподвижным концом от­резка является тот, для которого знак функции совпадает со знаком второй производной.

Если f (b) · f" (х) > 0, то неподвижен конец b, а в качест­ве начального приближения надо взять конец а [формулы (1) и (2)]. Если же f (а) · f" (х) > 0, то неподвижен конец а, а в качестве начального приближения следует взять конец b [формулы (3) и (4)].

Таким образом, в результате неоднократного применения формул (2) или (4) получаем монотонную последовательность х₁, х₂, ···, х_п - сходящуюся к значению корня ξ.

При оценке погрешности приближения можно пользовать­ся формулой

(5)

где ξ — точное значение корня, а х_п-1 и х_п — приближения к нему, полученные на (n — 1)-м и n-м шагах. Ею можно поль­зоваться, если выполнено условие

M ≤ 2m, где М= (6)

Метод Ньютона (метод касательных)

Другим итерационным методом является метод Нью­тона.

Пусть корень уравнения f (х) = 0 отделен на отрезке [a, b], причем f (x) и f″(x) непрерывны и сохраняют постоян­ные знаки на всем отрезке [a, b].

Геометрически смысл метода Ньютона состоит в том, что дуга кривой

у = f (x) заменяется касательной к этой кривой (отсюда и второе название этого метода — метод каса­тельных).

I случай: первая и вторая производные имеют одина­ковые знаки. Пусть f(а) < 0, f(b) > 0, f'(х) > 0, f″(х) > 0 рисунок 3, а) или f(а) > 0, f(b) < 0, f'(х) < 0, f″(х) < 0 рисунок 3, б). Проведем касательную к кривой у = f (x) в точке Β₀ (b; f (b)) и найдем абсциссу точки пересечения касательной с осью Ох:

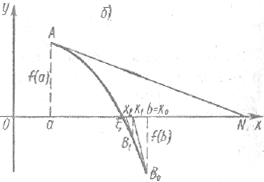
Рисунок 3

Известно, что уравнение касательной в точ­ке Β₀ (b; f (b)) имеет вид

у - f (b) = f´(b)(x - b). Полагая у = 0, x = x₁ получим (1)

Теперь корень уравнения находится на отрезке [а, х₂]. При­меняя снова метод Ньютона, проведем касательную к кривой в точке В₁(x₁; f(х₁)) и получим 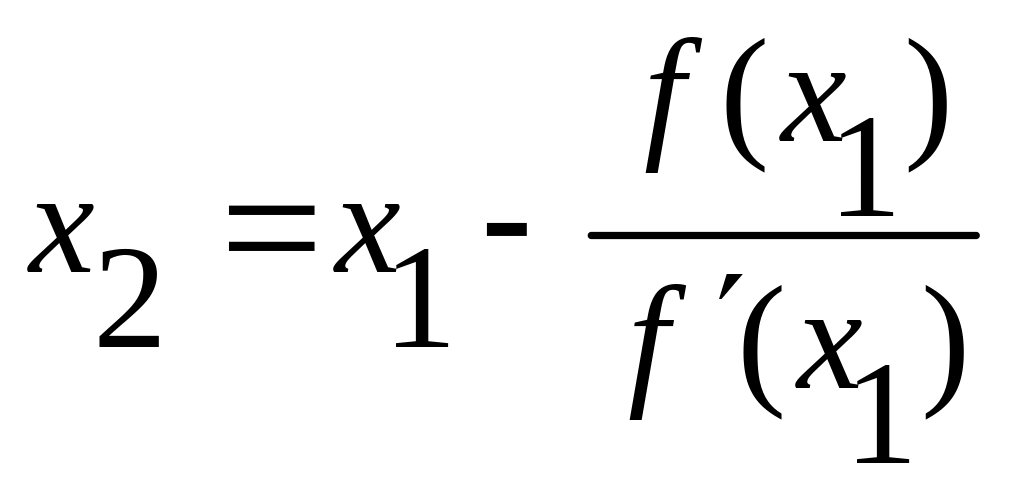. В общем виде (2)

Получаем последовательность приближенных значений x₁, x₂, ..., х_n, .... каждый последующий член которой ближе к корню ξ, чем предыдущий. Однако все х_п остаются больше ис­тинного корня ξ, т. е. х_п — приближенное значение корня ξ с избытком.

II с л у ч а й: первая и вторая производные имеют разные знаки. Пусть f(а) < 0, f(b) > 0, f'(х) > 0, f″(х) < 0 (рисунок 4,а) или f(а) > 0, f(b) < 0, f'(х) < 0, f″(х) > 0 (рисунок 4,б). Если провести касательную к кривой в точке В, то она пересечет ось абсцисс в точке, не принадлежащей отрезку [a, b]. Поэтому проведем касательную в точке А₀ (a; f (а)) и запишем ее уравнение для данного случая: y - f(a) = f'(a)(x - a).

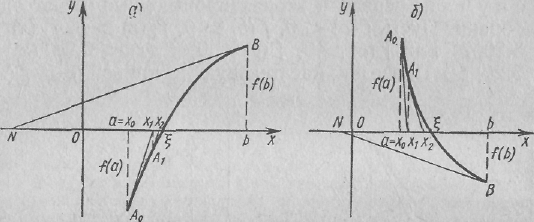
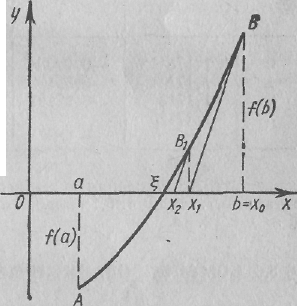
Рисунок 4 Рисунок 5

Полагая у = 0, х — х₁, находим (3)

Корень уравнения находится на отрезке [х1, b]. При­меняя снова метод Ньютона, проведем касательную к кривой в точке А1(x1; f(х1)) и получим .

В общем виде (4)

Таким образом получаем последовательность приближенных значений x₁, x₂, ..., х_n, .... каждый последующий член которой ближе к корню ξ, чем предыдущий. Однако все х_п остаются меньше ис­тинного корня ξ, т. е. х_п — приближенное значение корня ξ с недостатком.

Сравнивая эти формулы с ранее выведенным, замечаем, что они отличаются друг от друга только выбором начального приближения: в первом случае за х₀ принимался конец b от­резка, во втором — конец а.

При выборе начального приближения корня необходимо руководствоваться следующим правилом: за исходную точку следует выбирать тот конец отрезка [a, b], в котором знак функции совпадает со знаком второй производной. В пер­вом случае f(b) ∙ f″(х) > 0 и начальная точка b= х₀, во втором f(а) ∙ f″(х) > 0 и в качестве начального приближе­ния берем а = х₀.

Для оценки погрешности можно пользоваться общей фор­мулой

где (5)

(эта формула годится и для метода хорд).

В том случае, когда отрезок [[a, b] настолько мал, что на нем выполняется условие М2 < 2m1, где М2 = , a , точность приближения на n-м шаге оценивается следующим обра­зом: если |х_п — x_n-1| < ε, то |ξ — х_п | <ε².

Если производная f'(х) мало изменяется на отрезке [а, b], то для упрощения вы­числений можно пользоваться формулой 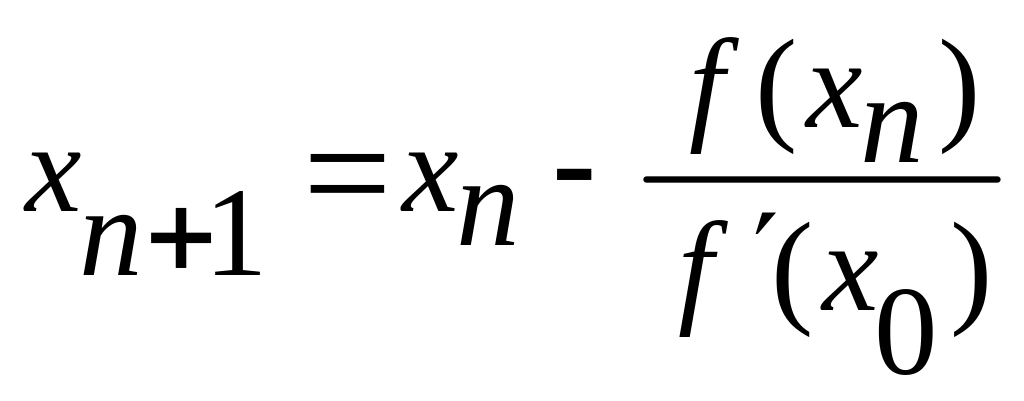(6)

т. е. значение производной в начальной точке достаточно вычислить только один раз. Геометрически это означает, что касательные в точках В_n (х_n; f(x_n)) заменяются прямыми, параллельными касательной, проведенной к кривой

у = f(x) в точке В₀ (х₀; f(x₀)) (рисунок 5).

Основная литература: 2[112-131], 1[138-156]

Контрольные вопросы:

1. Какие этапы необходимо пройти для получения значения корня нелинейного уравнения?

2. Что означает выражение отделить корень? Какие способы отделения корней вы знаете и в чем они заключаются?

3. В чем заключается теорема Штурма?

4. В чем заключается метод хорд?

5. В чем заключается метод касательных?

Лекция №3 Интерполяционные формулы Лагранжа. Конечные разности. Интерполяционные формулы Ньютона

Постановка задачи интерполирования. Конечные разности различных порядков. Интерполяционные формулы Ньютона, Гаусса, Лагранжа.

Постановка задачи интерполяции

Простейшая задача интерполирования заключается в следующем: на отрезке [a,b] заданы n+1 точки x₀, x₁, …, x_n , которые называются узлами интерполяции, и значения некоторой функции f(x) в этих точках f(x₀)=y₀ , f(x₁)=y₁ , ... , f(x_n)=y_n . Требуется построить функцию F(x) (интерполирующая функция), принадлежащая известному классу и принимающую в узлах интерполяции те же значения, что и функция f(x), т.е. F(x₀)= y₀ , F(x₁)= y₁ , . . . , F(x_n )=y_n .

При такой постановке задача имеет множество решений или совсем не иметь решения. Однако если вместо произвольной функции F(x) искать полином Р_n (x) степени не выше n такой, что Рn(x₀)= y₀ , Рn(x₁)= y₁ , . . . , Рn(x_n )=y_n , то задача становится однозначной.

Полученную интерполяционную формулу y = F(x) обычно используют для приближенного вычисления значений функции f(x) для значений аргумента, отличных от узлов интерполяции. Такая операция называется интерполированием функции f(x) .

Интерполяционная формула Лагранжа

Непосредственное определение коэффициентов интерполяционного многочлена связано с некоторыми вычислительными трудностями, поэтому при решении практических задач имеют дело со специальными видами интерполяционного многочлена.

Для произвольно заданных узлов интерполирования пользуются интерполяционной формулой Лагранжа.

где - множитель Лагранжа, важное свойство этих множителей .

Конечные разности

Пусть y = f(x) – заданная функция. x=h – фиксированная величина приращения аргумента (шаг). Тогда выражение y  f(x)= f(x+x) - f(x) называется первой конечной разностью функции y. Т. е. конечная разность первого порядка – разность между значениями функции в данном узле и в предыдущем. Конечные разности высших порядков определяются аналогично

ⁿy = (^n-1y) (n = 2, 3, …).

В математической литературе используются три типа конечных разностей: нисходящие разности для интерполяции вперед; восходящие разности для интерполирования назад; центральные разности для построения центральных интерполяционных формул.

Нисходящие, восходящие и центральные конечные разности связаны между собой следующими соотношениями:

для k=1 .

Интерполяционные формулы Ньютона

Если точка х* находится в начале или конце таблицы, то не всегда возможно выбрать достаточное количество узлов слева и справа от х* для построения необходимых конечных разностей. В этом случае используются специальные формы интерполяционного многочлена, так называемого многочлена Ньютона.

Для интерполирования в начале таблицы используется 1 интерполяционный многочлен Ньютона:

а) 1 интерполяционная формула Ньютона

Для интерполирования в конце таблицы используется 2 интерполяционный многочлен Ньютона:

б) 2 интерполяционная формула Ньютона

,

где q=(x - x_n)/h, h – шаг.

Интерполяционные формулы Гаусса

Для интерполирования в середине таблицы используются интерполяционные многочлены Гаусса

а) 1 интерполяционная формула Гаусса

где - центральная разность (2n-1)-го порядка в точке x_-n, а q=(x-x₀)/h - число шагов.

б) 2 интерполяционная формула Гаусса

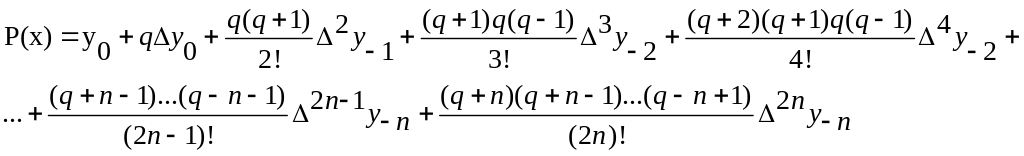
Основная литература: 2[497-561], 1[27-68]

Контрольные вопросы:

1. Объясните понятие термина интерполяция.

2. Интерполяционная формула Лагранжа.

3. Когда применяются интерполяционные формулы Ньютона?

4. Когда применяются интерполяционные формулы Гаусса?

Лекция №4 Численное интегрирование и численное дифференцирование

Численное интегрирование.

Пусть требуется вычислить определенный интеграл на интервале [a;b].

Далеко не всегда задача может быть решена аналитически. В частности, численное решение требуется в том случае, когда подынтегральная функция задана таблично. Для численного интегрирования подынтегральную функцию аппроксимируют какой-либо более простой функцией, интеграл от которой может быть вычислен. Обычно в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени метод численного интегрирования называют методом прямоугольников, в случае полинома первой степени – методом трапеций, в случае полинома второй степени – методом Симпсона. Все эти методы являются частными случаями квадратурных формул Ньютона-Котеса.

Формулы левых и правых прямоугольников соответственно , .

В методе трапеций подынтегральную функцию аппроксимируют полиномом первой степени, то есть прямой линией. Приближенное значение интеграла равно . При h=(b-a)/n формула трапеций будет

 h ((y₀+y_n)/2+y₁+y₂+…+y_n-1).

Формула Симпсона. Более точный результат можно получить, если заменить данную кривую параболой, проходящей через три точки.

при n=2 и h=(b-a)/2 – шаг.

Формула Симпсона

при n=2  (y₀+4y₂+y₄)

при n=4  (y₀+4y₁+2y₂+4y₃+y₄)

Квадратурные формулы Ньютона — Котеса

Пусть для данной функции y = f(x) требуется вычислить интеграл .

Выбрав шаг h=(b-a)/n, разобьем отрезок [а, b] с помощью равноотстоящих точек x₀=a, x_i=x₀+ih, x_n=b, на n равных частей, и пусть y_i=f(x_i)= f_i(a +ih) (i=0, 1, …, n)

Заменяя функцию y соответствующим интерполяционным полино­мом Лагранжа L_u(x), получим приближенную квадратурную формулу 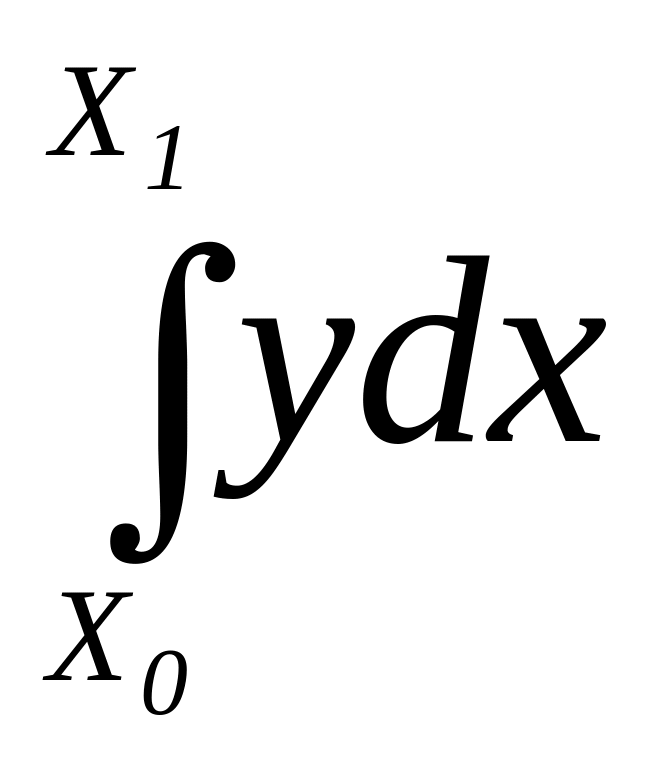= где А_i - некоторые постоянные коэффициенты. После некоторых преобразований квадратурная формула принимает вид =(b - a) , где H_i - постоянные, называемые коэффициентами Котеса. 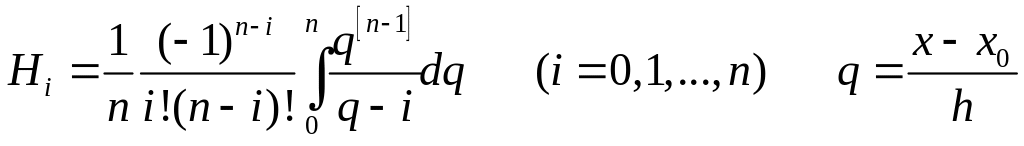. Нетрудно убедиться, что справедливы соотношения: 1) =1; 2) H_i = H_n-i.

После некоторых преобразований при n=3, получим квадратурную формулу Ньютона

- правило трех восьмых.

Коэффициенты Котеса

n										Общий знаменатель N
1	1	1								2
2	1	4	1							6
3	1	3	3	1						8
4	7	32	12	32	7					90
5	19	75	50	50	75	19				288
6	41	216	27	272	27	216	41			840
7	751	3577	1323	2989	2989	1323	3577	751		17280
8	989	5888	-928	10496	-4540	10496	-928	5888	989	28350

Для удобства записи коэффициенты Котеса для каждого n представлены в виде дробей

Квадратурные формулы Гаусса

 [C₁f(x₁)+ C₂f(x₂)+…+ C_nf(x_n)],

где x_i = + t_i (i=1, 2, …, n).

Значения C_i и t_i берут из таблицы квадратурных коэффициентов Гаусса

Численное дифференцирование.

При решении практических задач возникает необходимость получить значения производных различных порядков функции f , заданной в виде таблицы или сложного аналитического выражения. В этих случаях применяются методы численного дифференцирования. Простейшие выражения получаются в результате дифференцирования интерполяционных формул.

Формулы приближенного дифференцирования, основанные на первой интерполяционной формуле Ньютона.

Пусть имеем функцию y(x), заданную в равноотстоящих точках x_i (i=1, 2. …, n) отрезка [a,b] тогда для нахождения производных первого и второго порядка можно, заменяя функцию y приближенно на приближенный многочлен Ньютона

,

воспользоваться формулами

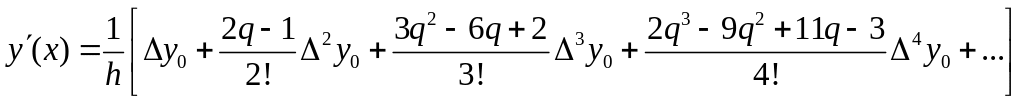
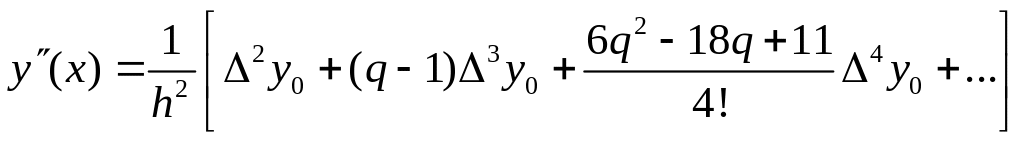
Таким же способом можно вычислить производные любого порядка.

Для нахождения производных в основных табличных точках x_i формулы упрощаются

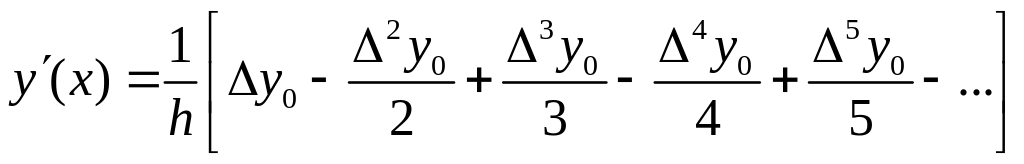
Основная литература: 2[577-589], 1[70-125]

Контрольные вопросы:

1. В чем заключается метод прямоугольников, метод трапеций и метод парабол для вычисления определенного интеграла?

2. Квадратурные формулы Ньютона — Котеса.

3. В чем заключается постановка задачи приближенного дифференцирования? Какие формулы приближенного дифференцирования вы знаете?

Лекция №5 Численные методы решения обыкновенных дифференциальных уравнений

Уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называется дифференциальным уравнением. Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то дифференциальное уравнение называется обыкновенным дифференциальным уравнением. Порядком дифференциального уравнения называется наивысший порядок производной (или дифференциала), входящей в уравнение. Обыкновенное дифференциальное уравнение n-го порядка в общем случае содержит независимую переменную, неизвестную функцию и ее производные или дифференциалы до n-го порядка включительно и имеет вид

(1) .

В этом уравнении х – независимая переменная, y – неизвестная функция, - производные этой функции.

Если левая часть уравнения (1) является многочленом по отношению к производной от неизвестной функции, то степень этого многочлена называется степенью дифференциального уравнения.

Дифференциальное уравнение n-го порядка, разрешенная относительно старшей производной, может быть записано в виде

(2)

Решением уравнения (2) называется всякая дифференциальная функция , удовлетворяющая этому уравнению. График решения обыкновенного дифференциального уравнения называется интегральной кривой этого уравнения. Частным решением дифференциального уравнения называется всякое решение, которое может быть получено из общего при определенных численных значениях произвольных постоянных, входящих в общее решение.

Пусть необходимо найти решение уравнения y=f(x,y) с начальным условием y(x₀)=y₀. Такая задача называется задачей Коши.

Задача Коши имеет единственное решение, если функция непрерывна в некоторой области и удовлетворяет в этой области условию Липшица , где N – постоянная Липшица, зависящая от a и b.

Существует множество методов решения обыкновенных дифференциальных уравнений, один из них метод Эйлера.

Разложим искомую функцию y(x) в ряд вблизи точки x₀ и ограничимся первыми двумя членами разложения y(x) = y(x₀) + y(x₀)(x - x₀)+…. Учтя уравнение и обозначив x - x₀=h, получаем y(x) = y(x₀) + f(x₀,y₀)x. Эту формулу можно применять многократно, находя значения функции во все новых и новых точках

y_i+1 = y_i + f(x_i,y_i)h.

Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера – метод первого порядка, то есть его точность растет линейно с уменьшением шага h.

y_i+1 = y_i +  y_i,  y_i = hf(x_i, y_i) (i=0, 1, 2, …) (метод Эйлера)

Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале. Среднее значение производной можно получить (конечно же только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала и использовать его для аппроксимации решения на всем интервале

x_i+1/2=x_i+h/2

y_i+1/2=y_i+h/2 f(x_i, y_i)

y_i+1/2=y_i+h f(x _i+1/2, y _i+1/2)

Можно также оценить среднее значение производной на интервале

=y_i+hf(x_i,y_i)

Такие модификации метода Эйлера имеет уже точность второго порядка.

Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутта следующие

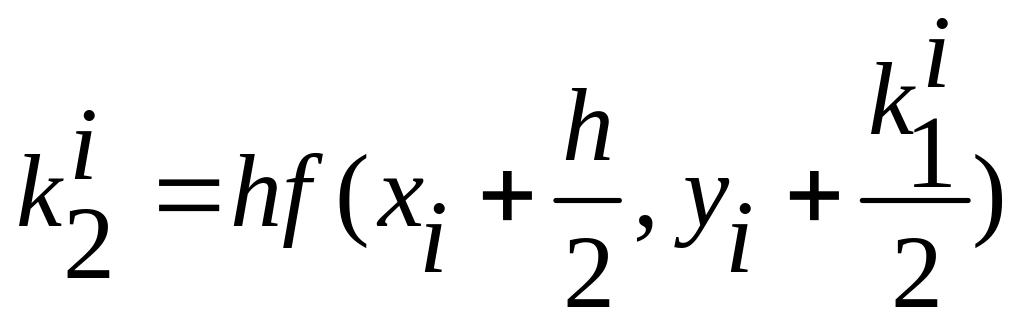
Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.

Основная литература: 3[121-156]

Контрольные вопросы:

1. Какое уравнение называется дифференциальным?

2. Какое уравнение называется обыкновенным дифференциальным уравнением?

3. Какая задача называется задачей Коши?

4. В чем заключается метод Эйлера?

5. В чем заключается метод Рунге-Кутта?

Лекция №6 Линейное программирование. Симплекс метод. Решение двойственных задач.

Общая и основная задачи линейного программирования

Общей задачей линейного программирования называется задача, которая состоит в определении максимального (минимального) значения функции

(1)

при условиях

(2)

(3)

(4)

где a_ij, b_i, c_j — заданные постоянные величины и k ≤ m.

Функция (1) называется целевой функцией (или линейной формой) задачи (1)—(4), а условия (2) — (4) —ограничениями данной задачи.

Стандартной (или симметричной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1) при выполнении условий (2) и (4), где k = m и l = п.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (1) при выполнении условий (3) и (4), где k = 0 и l = n.

Совокупность чисел X = (x₁, x₂,…, x_n), удовлетворяющих ограничениям задачи (2) — (4), называется допустимым решением (или планом).

План Х* = (x₁*, х₂*,…, х_n*), при котором целевая функция задачи (1) принимает свое максимальное (минимальное) значение, называется оптимальным.

Значение целевой функции (1) при плане X будем обозначать через F(X). Следовательно, X* — оптимальный план задачи, если для любого X выполняется неравенство F(X)≤F(X*) [соответственно F (X) ≥F (X*)].

Все эти три формы задачи линейного программирования эквивалентны, так как каждая из них с помощью несложных преобразований может быть переписана в форме другой задачи. Это означает, что если имеется способ нахождения решения одной из указанных задач, то тем самым может быть определен оптимальный план любой из трех задач.

Чтобы перейти от одной формы записи задачи линейного программирования к другой, нужно в общем случае уметь, во-первых, сводить задачу минимизации функции к задаче максимизации, во-вторых, переходить от ограничений-неравенств к ограничениям-равенствам и наоборот, в-третьих, заменять переменные, которые не подчинены условию неотрицательности.

В том случае, когда требуется найти минимум функции F = c₁x₁+c₂x₂+…+c_nx_n, можно перейти к нахождению максимума функции F₁ = -F = -(c₁x₁+c₂x₂+…+c_nx_n), поскольку min F = —max (—F).

Ограничение-неравенство исходной задачи линейного программирования, имеющее вид «≤», можно преобразовать в ограничение-равенство добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство вида «≥» — в ограничение-равенство вычитанием из его левой части дополнительной неотрицательной переменной. Таким образом, ограничение-неравенство a_i1x₁ +a_i2x₂+…+ а_inх_п ≤b_i,

преобразуется в ограничение-равенство a_i1x₁ +a_i2x₂+…+ а_inх_п + x_n+1, = b_i (x_n+1>0), (5)

а ограничение-неравенство a_i1x₁ +a_i2x₂+…+ а_inх_п ≥b_i, — в ограничение-равенство

a_i1x₁ +a_i2x₂+…+ а_inх_п - x_n+1, = b_i (x_n+1>0). (6)

В то же время каждое уравнение системы ограничений a_i1x₁+a_i2x₂ + ...+a_inx_n = b_i

можно записать в виде неравенств:

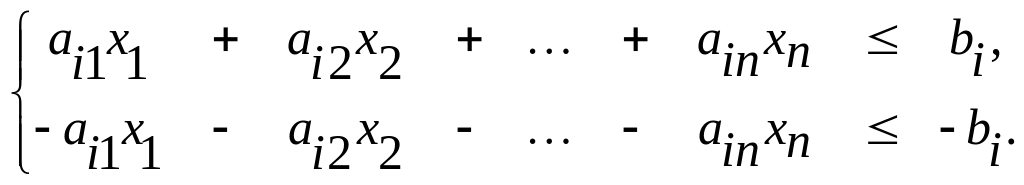(7)

Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств.

Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражается расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в форме основной, равно объему неиспользуемого соответствующего ресурса.

Отметим, наконец, что если переменная х_k не подчинена условию неотрицательности, то ее следует заменить двумя неотрицательными переменными u_k и v_k, приняв x_k = u_k - v_k.

Свойства основной задачи линейного программирования. Геометрическая интерпретация задачи линейного программирования

Рассмотрим основную задачу линейного программирования. Определить максимум функции F= , при условиях

Перепишем эту задачу в векторной форме: найти максимум функции F = CX (15)

при условиях x₁P₁ + x₂P₂ + ... + x_nP_n = P₀, (16) Х≥0, (17)

где С= (с₁; с₂, ...; c_n), Х = (х₁; х₂; ...; х_п); СХ — скалярное произ­ведение; Р₁, ..., Р_п и Р₀ — m-мерные вектор-столбцы, составлен­ные из коэффициентов при неизвестных и свободных членах си­стемы уравнений задачи:

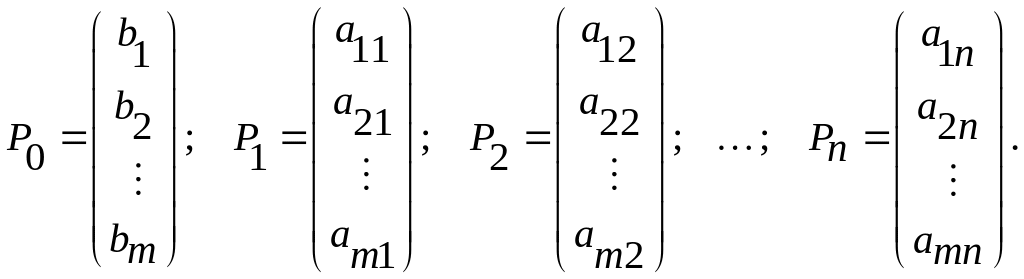
План Х= (х₁; х₂; ...; х_п) называется опорным планом основной задачи линейного программирования, если система векторов P_j входящих в разложение (16) с положи­тельными коэффициентами х,, линейно независима.

Так как векторы P_j являются m-мерными, то из определения опорного плана следует, что число его положительных компонент не может быть больше, чем т.

Опорный план называется невырож­денным, если он содержит ровно т положительных компонент, в противном случае он называется вырожденным.

Свойства основной задачи линейного программирования (15) - (17) тесным образом связаны со свойствами выпуклых множеств.

Пусть X₁, X₂, ..., Х_п — произвольные точки евклидова пространства Е_п. Выпуклой линейной комбинацией этих точек называется сумма a₁X₁ + a₂X₂ +... + а_пХ_п, где а_i — произвольные неотрицательные числа, сумма которых равна 1:

Множество называется выпуклым, если вместе с любыми двумя своими точками оно содержит и их произвольную выпуклую линейную комбинацию.

Точка X выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации каких-нибудь двух других различных точек данного множества.

Теорема 1.1. Множество планов основной задачи линейного программирования является выпуклым (если оно не пусто).

Непустое множество планов основ­ной задачи линейного программирования называется многогранником решений, а всякая угловая точка многогранника решений — вершиной.

Теорема 1.2. Если основная задача линейного программиро­вания имеет оптимальный план, то максимальное значение целевая функция задачи принимает в одной из вершин многогран­ника решений. Если максимальное значение целевая функция задачи принимает более чем в одной вершине, то она принимает его во всякой точке, являющейся выпуклой линейной комбинацией этих вершин.

Теорема 1.3. Если система векторов Р₁, Р₂, …, P_k (k≤n) в разложении (16) линейно независима и такова, что x₁P₁+x₂P₂ + ... + x_kP_k = P₀, (18)

где все x_j≥0, то точка Х= (х₁; х₂; ...; x_k; 0; ...; 0) является вершиной многогранника решений.

Теорема 1.4. Если X= (x₁; x₂; ...; х_п) — вершина многогранника решений, то векторы P_j, соответствующие положитель­ным x_j в разложении (16), линейно независимы.

Сформулированные теоремы позволяют сделать следующие выводы.

Непустое множество планов основной задачи линейного про­граммирования образует выпуклый многогранник. Каждая вер­шина этого многогранника определяет опорный план. В одной из вершин многогранника решений (т. е. для одного из опорных планов) значение целевой функции является максимальным (при условии, что функция ограничена сверху на множестве планов). Если максимальное значение функция принимает более чем в одной вершине, то это же значение она принимает в любой точке, являющейся выпуклой линейной комбинацией данных вершин.

Вершину многогранника решений, в которой целевая функция принимает максимальное значение, найти сравнительно просто, если задача, записанная в форме стандартной, содержит не более двух переменных или задача, записанная в форме основной, содержит не более двух свободных переменных, т. е. п - r ≤ 2, где n — число переменных, r — ранг матрицы, составленной из коэффициентов в системе ограничений задачи.

Найдем решение задачи, состоящей в определении максимального значения функции

F=c₁x₁+c₂x₂ (19)

при условиях

a_i1x₁ + a_i2x₂ ≤ b_i ( ), (20)

х_j ≥ 0 (j = 1,2). (21)

Каждое из неравенств (20), (21) системы ограничений задачи геометрически определяет полуплоскость соответственно с граничными прямыми a_i1x₁ + a_i2x₂ = b_i ( ), x₁ =0 и x₂ = 0. В том случае, если система неравенств (20), (21) совместна, область ее решений есть множество точек, принадлежащих всем указанным полуплоскостям. Так как множество точек пересечения данных полуплоскостей — выпуклое, то областью допустимых решений задачи (19) — (21) является выпуклое множество, которое называется многоугольником решений (введенный ранее термин «многогранник решений» обычно употребляется, если n≥3). Стороны этого многоугольника лежат на прямых, уравнения которых получаются из исходной системы ограничений заменой знаков неравенств на знаки точных равенств.

Таким образом, исходная задача линейного программирования состоит в нахождении такой точки многоугольника решений, в которой целевая функция F принимает максимальное значение. Эта точка существует тогда, когда многоугольник решений не пуст и на нем целевая функция ограничена сверху. При указанных условиях в одной из вершин многоугольника решений целевая функция принимает максимальное значение. Для определения данной вершины построим линию уровня c₁x₁+c₂x₂ = h (где h — некоторая постоянная), проходящую через многоугольник решений, и будем передвигать ее в направлении вектора С = (c₁;c₂) до тех пор, пока она не пройдет через последнюю ее общую точку с многоугольником решений. Координаты указанной точки и определяют оптимальный план данной задачи.

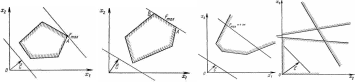
Необходимо отметить, что при нахождении ее решения задачи (9) — (21),могут встретиться случаи, изображенные на рисунок 6 —9. Рисунок 6 характеризует такой случай, когда целевая функция принимает максимальное значение в единственной точке А. Из рисунка 7 видно, что максимальное значение целевая функция принимает в любой точке отрезка АВ. На рисунке 8 изображен случай, когда целевая функция не ограничена сверху на множестве допустимых решений, а на рисунке 9 — случай, когда система ограничений задачи несовместна.

Отметим, что нахождение минимального значения линейной функции при данной системе ограничений отличается от нахождения ее максимального значения при тех же ограничениях лишь тем, что линия уровня c₁x₁ + c₂x₂ = h передвигается не в направлении вектора С=(c₁; с₂), а в противоположном направлении. Таким образом, отмеченные выше случаи, встречающиеся при нахождении максимального значения целевой функции, имеют место и при определении ее минимального значения.

Итак, нахождение решения задачи линейного программиро­вания (19)—(21) на основе ее геометрической интерпретации включает следующие этапы:

1. Строят прямые, уравнения которых получаются в результате замены в ограничениях (20) и (21) знаков неравенств на знаки точных равенств.

2. Находят полуплоскости, определяемые каждым из ограничений задачи.

1. Находят многоугольник решений.

2. Строят вектор С = (c₁; c₂).

3. Строят прямую c₁x₁ + c₂x₂ = h, проходящую через многоугольник решений.

4. Передвигают прямую с₁x₁ +с₂x₂ = h в направлении вектора , в результате чего либо находят точку (точки), в которой целевая функция принимает максимальное значение, либо устанавливают неограниченность сверху функции на множестве планов.

5. О пределяют координаты точки максимума функции и вычисляют значение целевой функции в этой точке.

Рисунок 6 Рисунок 7 Рисунок 8 Рисунок 9

Нахождение решения задачи линейного программирования

Решение любой задачи линейного программирования можно найти либо симплексным методом, либо методом искусственного базиса. Прежде чем применять один из указанных методов, следует записать исходную задачу в форме основной задачи линейного программирования, если она не имеет такой формы записи.

Симплексный метод. Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Указанный переход возможен, если известен какой-нибудь исходный опорный план. Рассмотрим задачу, для которой этот план можно непосредственно записать.

Пусть требуется найти максимальное значение функции

F = c₁x₁+c₂x₂+…+c_nx_n

при условиях

х₁+ а_{1 т+1}х_т+1 + … + a_1nх_п = b₁,

x₂ + a_{2 m+1}x_m+1 + … + a_2nx_n = b₂,

. . . . . . . . . . . .

x_m + a_{m m+1}x_m+1+ ... +a_mnx_n = b_m,

х_j>0 ( )

Здесь а_ij, b_i и с_j ( ; ) — заданные постоянные числа (т<п и bi>0).

Векторная форма данной задачи имеет следующий вид: найти максимум функции

F=

при условиях

x₁P₁+x₂P₂+ …+х_тР_m+ ... + х_nР_n = Р₀,

х_j>0 ( ),

где

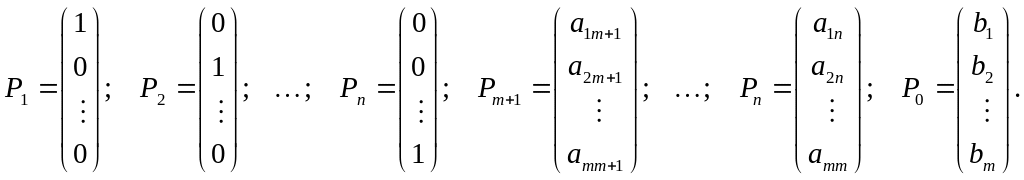
Так как b₁P₁ + b₂P₂+…+b_mP_m = P₀ , то по определению опорного плана Х= (b₁; b₂; ...; b_m; 0; ...; 0) является опорным планом данной задачи (последние п - т компонент вектора X равны нулю). Этот план определяется системой единичных векторов Р₁, Р₂, ..., Р_т, которые образуют базис m-мерного пространства. Поэтому каждый из векторов Р₁, Р₂, ..., Р_n, а также вектор Р₀ могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть Положим . Так как векторы Р₁, Р₂, …, Р_т — единичные, то х_ij = а_ij и , а .

Теорема 1.5 (признак оптимальности опорного плана). Опорный план Х*= (x*₁; x*₂; ... ; х*_т; 0; 0; ...; 0) задачи (22) — (24) является оптимальным, если D_j ≥ 0 (для любого j ( ).

Теорема 1.6. Если D_k < 0 для некоторого j = k и среди чисел a_ik ( ) нет положительных ( a_ik ≤ 0), то целевая функция (22) задачи (22) — (24) не ограничена на множестве ее планов.

Теорема 1.7. Если опорный план X задачи (22) — (24) не вырожден и ∆_k < 0, но среди чисел a_ik есть положительные (не все a_ik ≤ 0), то существует опорный план X' такой, что F (Х')> >F (X).

Таблица 1.3

i

Базис

Сб

Р0

С1

C2

…

Cr

…

сm

Сm+1

…

Ck

…

Cn

Р1

P2

…

Рr

…

Рm

Рm+1

…

Pk

…

Pn

1

P1

c1

b1

1

0

…

0

…

0

a1m+1

…

a1k

…

a1n

2

Р2

с2

b2

0

1

…

0

…

0

a2m+1

…

a2k

…

a2n

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

r

Рr

cr

br

0

0

…

1

…

0

arm+1

…

ark

…

arn

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

т

Рт

cm

bт

0

0

…

0

…

1

amm+1

…

amk

…

amn

m+1

0

0

…

0

…

0

∆m+1

…

∆k

…

∆n

Таблица 1.4

i

Базис

C6

P0

С1

C2

…

Cr

…

Cm

Cm+1

…

Ck

…

Cn

P1

P2

…

Pr

…

Pm

Pm+1

…

Pk

…

Pn

1

P1

c1

b'1

1

0

…

a'1r

…

0

a'1m+1

…

0

…

a'1n

2

P2

c2

b'2

0

1

…

a'2r

…

0

a'2m+1

…

0

…

a'2n

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

r

Pk

ck

b'k

0

0

…

a'rr

…

0

a'rm+1

…

1

…

a'rn

…

…

…

…

…

…

…

…

…

…

…

…

…

…

…

m

cm

b'm

0

0

…

a'mr

…

1

a'mm+l

…

0

…

m+1

F0

0

0

…

z'r - cr

…

0

z'm+1 - cm+1

…

0

…

z'n - cn

Сформулированные теоремы позволяют проверить, является ли найденный опорный план оптимальным, и выявить целесообразность перехода к новому опорному плану.

Исследование опорного плана на оптимальность, а также дальнейший вычислительный процесс удобнее вести, если условия задачи и первоначальные данные, полученные после определения исходного опорного плана, записать так, как показано в таблице 1.3.

В столбце С_б этой таблицы записывают коэффициенты при неизвестных целевой функции, имеющие те же индексы, что и векторы данного базиса.

В столбце Р_о записывают положительные компоненты исходного опорного плана, в нем же в результате вычислений получают положительные компоненты оптимального плана. Столбцы векторов Р_j представляют собой коэффициенты разложения этих векторов по векторам данного базиса.

В таблице 1.3 первые m строк определяются исходными данными задачи, а показатели (m+1)-й строки вычисляют. В этой строке в столбце вектора Р_о записывают значение целевой функции, которое она принимает при данном опорном плане, а в столбце вектора Р_j — значение ∆_j = z_j – c_j.

Значение z_j находится как скалярное произведение вектора Р_j( ) на вектор С_б=(с₁; с₂; ...; с_т): z_j= ( ).

Значение F₀ равно скалярному произведению вектора Р₀ на вектор С_б: .

После заполнения таблицы 1.3 исходный опорный план проверяют на оптимальность. Для этого просматривают элементы (m+1)-й строки таблицы. В результате может иметь место один из следующих трех случаев:

1. ∆_j ≥ 0 для j = m + 1, m + 2, ..., п (при , z_j = с_j). По этому в данном случае числа ∆_j ≥0 для всех j от 1 до n;

2. ∆_j < 0 для некоторого j, и все соответствующие этому индексу величины a_ij ≤ 0 ( );

3. ∆_j < 0 для некоторых индексов j, и для каждого такого j по крайней мере одно из чисел a_ij положительно.

В первом случае на основании признака оптимальности исходный опорный план является оптимальным. Во втором случае целевая функция не ограничена сверху на множестве планов, а в третьем случае можно перейти от исходного плана к новому опорному плану, при котором значение целевой функции увеличится. Этот переход от одного опорного плана к другому осуществляется исключением из исходного базиса какого-нибудь из векторов и введением в него нового вектора. В качестве вектора, вводимого в базис, можно взять любой из векторов Р_j, имеющий индекс j, для которого ∆_j < 0. Пусть, например, ∆_j < 0 и решено ввести в базис вектор Р_k.

Для определения вектора, подлежащего исключению из базиса, находят min (b,/ a_ik) для всех a_jk > 0. Пусть этот минимум достигается при i = r. Тогда из базиса исключают вектор Р_r, а число a_rk называют разрешающим элементом.

Столбец и строку, на пересечении которых находится разрешающий элемент, называют направляющими.

После выделения направляющей строки и направляющего столбца находят новый опорный план и коэффициенты разложения векторов Р_j через векторы нового базиса, соответствующего новому опорному плану. Это легко реализовать, если воспользоваться методом Жордана—Гаусса. При этом можно показать, что положительные компоненты нового опорного плана вычисляются по формулам

(25)

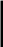а коэффициенты разложения векторов Р_j через векторы нового базиса, соответствующего новому опорному плану, — по формулам

(26)

После вычисления b'_i и а'_ij согласно формулам (25) и (26) их значения заносят в табл. 1.4. Элементы (m+1)-й строки этой таблицы могут быть вычислены либо по формулам

F'0 = F0 - (br/ark)∆k , (27)

∆'j =∆j - (arj/ark) ∆k , (28)

либо на основании их определения.

Наличие двух способов нахождения элементов (m+1)-й строки позволяет осуществлять контроль правильности проводимых вычислений.

Из формулы (27) следует, что при переходе от одного опорного плана к другому наиболее целесообразно ввести в базис вектор Р_j, имеющий индекс j, при котором максимальным по абсолютной величине является число (b_r/a_r,) ∆_j (∆_j < 0, а_rj >0). Однако с целью упрощения вычислительного процесса в дальнейшем будем вектор, вводимый в базис, определять, исходя из максимальной абсолютной величины отрицательных чисел ∆_j. Если же таких чисел несколько, то в базис будем вводить вектор, имеющий такой же индекс, как и максимальное из чисел c_j определяемых данными числами ∆_j (∆_j < 0).

Итак, переход от одного опорного плана к другому сводится к переходу от одной симплекс-таблицы к другой. Элементы новой симплекс-таблицы можно вычислить как с помощью рекуррентных формул (25) — (28), так и по правилам, непосредственно вытекающим из них. Эти правила состоят в следующем.

В столбцах векторов, входящих в базис, на пересечении строк и столбцов одноименных векторов проставляются единицы, а все остальные элементы данных столбцов полагают равными нулю.

Элементы векторов Р₀ и Р_j в строке новой симплекс-таблицы, в которой записан вектор, вводимый в базис, получают из элементов этой же строки исходной таблицы делением их на величину разрешающего элемента. В столбце С_б в строке вводимого вектора проставляют величину с_k, где k — индекс вводимого вектора.

Остальные элементы столбцов вектора Р₀ и Р_j новой симплекс-таблицы вычисляют по правилу треугольника. Для вычисления какого-нибудь из этих элементов находят три числа:

1) число, стоящее в исходной симплекс-таблице на месте искомого элемента новой симплекс-таблицы;

2. число, стоящее в исходной симплекс-таблице на пересечении строки, в которой находится искомый элемент новой симплекс-таблицы, и столбца, соответствующего вектору, вводимому в базис;

3. число, стоящее в новой симплекс-таблице на пересечении столбца, в котором стоит искомый элемент, и строки вновь вводимого в базис вектора.

Эти три числа образуют своеобразный треугольник, две вершины которого соответствуют числам, находящимся в исходной симплекс-таблице, а третья — числу, находящемуся в новой симплекс-таблице. Для определения искомого элемента новой симплекс-таблицы из первого числа вычитают произведение второго и третьего.

После заполнения новой симплекс-таблицы просматривают элементы (m+1)-й строки. Если все z_j – с_j ≥ 0, то новый опорный план является оптимальным. Если же среди указанных чисел имеются отрицательные, то, используя описанную выше последовательность действий, находят новый опорный план. Этот процесс продолжают до тех пор, пока либо не получают оптимальный план задачи, либо не устанавливают ее неразрешимость.

При нахождении решения задачи линейного программирования мы предполагали, что эта задача имеет опорные планы и каждый такой план является невырожденным. Если же задача имеет вырожденные опорные планы, то на одной из итераций одна или несколько переменных опорного плана могут оказаться равными нулю. Таким образом, при переходе от одного опорного плана к другому значение функции может остаться прежним. Более того, возможен случай, когда функция сохраняет свое значение в течение нескольких итераций, а также возможен возврат к первоначальному базису. В последнем случае обычно говорят, что произошло зацикливание. Однако при решении практических задач этот случай встречается очень редко, поэтому мы на нем останавливаться не будем.

Итак, нахождение оптимального плана симплексным методом включает следующие этапы:

1. Находят опорный план.

2. Составляют симплекс-таблицу.

3. Выясняют, имеется ли хотя бы одно отрицательное число ∆_j. Если нет, то найденный опорный план оптимален. Если же среди чисел ∆_j имеются отрицательные, то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану.

4. Находят направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом ∆_j , а направляющая строка — минимальным из отношений компонент столбца вектора Р₀ к положительным компонентам направляющего столбца.

5. По формулам (25) — (28) определяют положительные компоненты нового опорного плана, коэффициенты разложения векторов Р_j по векторам нового базиса и числа F'₀, ∆'_j. Все эти числа записываются в новой симплекс-таблице.

6. Проверяют найденный опорный план на оптимальность. Если план не оптимален и необходимо перейти к новому опорному плану, то возвращаются к этапу 4, а в случае получения оптимального плана или установления неразрешимости процесс решения задачи заканчивают.

Основная литература: 1[944-1000], 7[6-87]

Контрольные вопросы:

1. Какая задача называется общей задачей линейного программирования?

2. Что является решением задачи линейного программирования?

3. Объясните геометрическую интерпретацию задач линейного программирования.

4. В чем заключается симплексный метод решения задачи линейного программирования?

Лекция №7 Транспортная задача

Математическая постановка задачи. Общая постановка тран­спортной задачи состоит в определении оптимального плана пе­ревозок некоторого однородного груза из т пунктов отправления A1, А2, ..., Аm в п пунктов назначения B1, В2, ..., Вп. При этом в ка­честве критерия оптимальности обычно берется либо минималь­ная стоимость перевозок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве кри­терия оптимальности которой взята минимальная стоимость пере­возок всего груза. Обозначим через Сij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через а, — запасы груза в i-м пункте отправления, через bj — потребно­сти в грузе в j-м пункте назначения, а через xij — количество еди­ниц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции

(1)

при условиях

(2)

и

(3)

(4)

Поскольку переменные x_ij ( ; ) удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза в каждый из пунктов назначения, вывоз имеющегося груза из всех пунктов отправления, а также исключаются обратные перевозки.

Определение 2.1. Всякое неотрицательное решение си­стем линейных уравнений (2) и (3), определяемое матрицей X = (x_ij)(i= l,m; j==1,n), называется планом транспортной за­дачи.

Определение 2.2. План X* = (x*_ij) ( ; ), при котором функция (1) принимает свое минимальное значение, на­зывается оптимальным планом транспортной задачи.

Обычно исходные данные транспортной задачи записывают в виде таблицы.

Пункты отправ­ления	Пункты назначения								Запасы
	В1		. . .	Bj		. . .	Bn
A1	c11	x11		c1j	x1j	. . .	c1n	x1n	a1
. . .	. . .		. . .	. . .		. . .	. . .		. . .
Ai	ci1	xi1	. . .	cij	xij	. . .	cin	xin	ai
. . .	. . .		. . .	. . .		. . .	. . .		. . .
Am	cm1	xт1	. . .	cmj	xmj		cmn	xmn	am
Потребности	b1		. . .	bj		. . .	bn

Очевидно, общее наличие груза у поставщиков равно , а общая потребность в грузе в пунктах назначения равна единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т. е.

= , (5)

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

Теорема 2.1. Для разрешимости транспортной задачи необхо­димо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т. е. чтобы выполнялось равенство (5).

В случае превышения запаса над потребностью, т. е. > , вводится фиктивный (n+1)-й пункт назначения с потребностью b_n+1= - и соответствующие тарифы считаются равными нулю: c_in+1 = 0 . Полученная зада­ча является транспортной задачей, для которой выполняется равенство (5).

Аналогично, при < вводится фиктивный (m+1)-й пункт отправления с запасом груза a_{m+ 1} = - и тарифы полагаются равными нулю: с_{m+1 j} = 0 ( ). Этим задача сво­дится к обычной транспортной задаче, из оптимального плана которой получается оптимальный план исходной задачи. В даль­нейшем будем рассматривать закрытую модель транспортной за­дачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так» чтобы выполнялось равенство (5).

Число переменных х_ij в транспортной задаче с т пунктами отправления и п пунктами назначения равно пт, а число уравне­ний в системах (2) и (3) равно n + m. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно п+т-1. Следовательно, опорный план транс­портной задачи может иметь не более п+т-1 отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля компонент равно в точности п+т-1, то план является невырожденным, а если меньше — то вырожденным.

Для определения опорного плана существует несколько ме­тодов. Три из них — метод северо-западного угла, метод мини­мального элемента и метод аппроксимации Фогеля — рассматри­ваются ниже.

Как и для всякой задачи линейного программирования, опти­мальный план транспортной задачи является и опорным планом.

Для определения оптимального плана транспортной задачи можно использовать изложенные выше методы. Однако ввиду исключительной практической важности этой задачи и специ­фики ее ограничений [каждая неизвестная входит лишь в два уравнения систем (2) и (3) и коэффициенты при неизвестных равны единице] для определения оптимального плана транспорт­ной задачи разработаны специальные методы. Два из них — метод потенциалов и метод дифференциальных рент — рассмо­трены ниже.

Математическая постановка данной транс­портной задачи состоит в нахождении такого неотрицательного решения системы линейных уравнений, при котором целевая функция принимает минимальное значение.

Определение опорного плана транспортной задачи. Как и при решении задачи линейного программирования симплексным методом, определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Этот план, как уже отмечалось выше, находят методом северо-запад­ного угла, методом минимального элемента или методом аппрок­симации Фогеля. Сущность этих методов состоит в том, что опор­ный план находят последовательно за п+т-1 шагов, на каж­дом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспе­чивает полностью либо удовлетворение потребности в грузе од­ного из пунктов назначения (того, в столбце которого находится заполненная клетка), либо вывоз груза из одного из пунктов отправления (из того, в строке которого находится заполняемая клетка).

В первом случае временно исключают из рассмотрения стол­бец, содержащий заполненную на данном шаге клетку, и рассма­тривают задачу, таблица условий которой содержит на один стол­бец меньше, чем было перед этим шагом, но то же количество строк и соответственно измененные запасы груза в одном из пунктов отправления (в том, за счет запаса которого была удовлет­ворена потребность в грузе пункта назначения на данном шаге). Во втором случае временно исключают из рассмотрения строку, содержащую заполненную клетку, и считают, что таблица усло­вий имеет на одну строку меньше при неизменном количестве столбцов и при соответствующем изменении потребности в грузе в пункте назначения, в столбце которого находится заполняемая клетка.

После того как проделаны т+п-2 описанных выше шагов, получают задачу с одним пунктом отправления и одним пунк­том назначения. При этом останется свободной только одна клетка, а запасы оставшегося пункта отправления будут равны потребностям оставшегося пункта назначения. Заполнив эту клетку, тем самым делают (п+т -1)-й шаг и получают искомый опорный план. Следует заметить, что на некотором шаге (но не на последнем) может оказаться, что потребности очередного пункта назначения равны запасам очередного пункта отправле­ния. В этом случае также временно исключают из рассмотрения либо столбец, либо строку (что-нибудь одно). Таким образом, либо запасы соответствующего пункта отправления, либо потреб­ности данного пункта назначения считают равными нулю. Этот нуль записывают в очередную заполняемую клетку. Указанные выше условия гарантируют получение п+т-1 занятых клеток, в которых стоят компоненты опорного плана, что является исход­ным условием для проверки последнего на оптимальность и на­хождения оптимального плана.

Метод северо-западного угла. При нахождении опорного плана транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначе­ния. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного х₁₁ («северо-западный угол») и заканчивается клеткой для неизвестного х_тп, т. е. идет как бы по диагонали таблицы.

Метод минимального элемента. В методе се­веро-западного угла на каждом шаге потребности первого из оставшихся пунктов назначения удовлетворялись за счет запа­сов первого из оставшихся пунктов отправления. Очевидно, выбор пунктов назначения и отправления целесообразно произ­водить, ориентируясь на тарифы перевозок, а именно: на каждом шаге следует выбирать какую-нибудь клетку, отвечающую мини­мальному тарифу (если таких клеток несколько, то следует вы­брать любую из них), и рассмотреть пункты назначения и отправ­ления, соответствующие выбранной клетке. Сущность метода минимального элемента и состоит в выборе клетки с минималь­ным тарифом. Следует отметить, что этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому наиболее целесообразно опорный план транспортной задачи находить методом минималь­ного элемента.

Метод аппроксимации Фогеля. При определении оптимального плана транспортной задачи методом аппрок­симации Фогеля на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них мини­мальными тарифами. Эти разности записывают в специально от­веденных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают минимальную; В строке (или в столбце), которой данная разность соответствует, опреде­ляют минимальный тариф. Клетку, в которой он записан, запол­няют на данной итерации.

Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наи­большей разности между двумя минимальными тарифами, нахо­дящимися в данном столбце (строке).

Основная литература: 7[134-154]

Контрольные вопросы:

1. В чем заключается математическая постановка транспортной задачи?

2. Каким образом можно определить опорный план транспортной задачи?