2.7 Примерный перечень тем рефератов

1 Вычисление определителя матрицы с помощью LU-разложения.

2 Вычисление обратной матрицы с помощью LU-разложения.

3 Схема Холецкого.

4 Метод релаксации для решения систем линейных уравнений

5 Метод наискорейшего спуска (метод градиента).

6 Интерполяционные формулы Гаусса

7 Погрешность результата численного решения задач.

8 Нахождение кор­ней уравнения методом обратного интерполирования.

9 Численные методы решения задачи Коши. Метод Эйлера.

10 Решение транспортных задач методом потенциалов.

11 Алгебра матриц

12 Определение собственных значений и собственных векторов матрицы

13 Метод Монте-Карло

14 Метод Крылова для развертывания характеристического определителя

15 Вычисление собственных векторов методом Крылова

2.8 Тестовые задания для самоконтроля с указанием ключей правильных ответов

1. Решением системы линейных уравнений называется

a) лю­бая совокупность чисел α₁, α₂, ..., α_n, которая, будучи подстав­ленной на место неизвестных x₁, x₂, ..., х_п в уравнения данной системы, обращает все эти уравнения в тождества.

b) лю­бая совокупность чисел α₁, α₂, ..., α_n, которая, будучи подстав­ленной на место неизвестных x₁, x₂, ..., х_п в уравнения данной системы, обращает все эти уравнения в неравенства.

c) совокупность чисел α₁, α₂, ..., α_n, которая, будучи подстав­ленной на место неизвестных x₁, x₂, ..., х_п в уравнения данной системы, обращает все эти уравнения в строгие неравенства.

d) совокупность чисел α₁, α₂, ..., α_n, которая, будучи подстав­ленной на место неизвестных x₁, x₂, ..., х_п в уравнения данной системы, обращает все эти уравнения в нестрогие неравенства.

e) число α, которое, будучи подставлено на место неизвестного x₁ в уравнения данной системы, обращает все эти уравнения в тождества.

2. Система линейных уравнений имеющая решение называется:

a) тождественной

b) приближенной

c) совместной

d) неопределенной

e) несовместной

3. Система линейных уравнений не имеющая решения называется:

a) тождественной

b) приближенной

c) совместной

d) неопределенной

e) несовместной

4. Совместная система линейных уравнений имеющая одно решение называется:

a) тождественной

b) определенной

c) совместной

d) неопределенной

e) несовместной

5.Совместная система линейных уравнений имеющая более одного решения называется:

a) тождественной

b) определенной

c) совместной

d) неопределенной

e) несовместной

6. Для решения систем линейных уравнений существует множество методов, которые подразделяются на точные и приближенные. К точным методам относятся методы:

a) итераций

b) Зейделя

c) хорд

d) Гаусса

e) Ньютона

7. Для решения систем линейных уравнений существует множество методов, которые подразделяются на точные и приближенные. К приближенным методам относятся методы:

a) главных элементов

b) Зейделя

c) хорд

d) Гаусса

e) Ньютона

8. Процесс нахождения приближенных значений корней нелинейных уравнений разбивается на два этапа: отделение корней и уточнение корней до заданной степени точности. Для определения числа действительных корней и отделения корней существует теорема Штурма. Последовательность следующих функций называется системой Штурма. Укажите лишнее:

a) P_n(x), P_n(x),

b) P_n(x),

c) R₁(x),

d) R₂(x),

e) R₃(x), …, R_n=const

9. Для решения нелинейных уравнений и систем нелинейных уравнений существует метод:

a) итераций Крамера

b) Зейделя - Крамера

c) хорд

d) Гаусса - Зейделя

e) главных элементов

10. Для решения нелинейных уравнений и систем нелинейных уравнений существует метод:

a) Ньютона

b) Зейделя - Крамера

c) Крамера

d) Гаусса - Зейделя

e) главных элементов

11. В методе хорд для уточнения корня используются разные формулы в зависимости от того какой конец отрезка является неподвижным. Неподвижным концом от­резка является тот, для которого:

a) знак функции не совпадает со знаком второй производной

b) знак функции совпадает со знаком второй производной

c) знак функции совпадает со знаком первой производной

d) знак третьей производной совпадает со знаком второй производной

e) знак функции не совпадает со знаком первой производной

12. В методе хорд для уточнения корня, когда первая и вторая производные имеют одина­ковые знаки, используются формулы:

a)

b)

c)

d)

e)

13. В методе хорд для уточнения корня, когда первая и вторая производные имеют разные знаки, используются формулы:

a)

b)

c)

d)

e)

14. В методе Ньютона для уточнения корня уравнения f (х) = 0 на отрезке [a, b] используется формула . Для получения первого приближения, когда первая и вторая производные имеют одина­ковые знаки:

a)

b)

c)

d)

e)

15. В методе Ньютона для уточнения корня уравнения f (х) = 0 на отрезке [a, b] используется формула . Для получения первого приближения, когда первая и вторая производные имеют разные знаки:

a)

b)

c)

d)

e)

16. Интерполяцией называется:

a) вычисление приближенного значений функции f(x) для значений аргумента, в узлах интерполяции

b) вычисление приближенного значений функции f(x) для значений аргумента, отличных от узлов интерполяции

c) нахождение аналитического выражения функции проходящей через узлы интерполяции

d) нахождение аналитического выражения функции не проходящей через узлы интерполяции

e) нахождение аналитического выражения функции отстоящей от узлов интерполяции на заданном расстоянии

17. Интерполированием функции f(x) называется операция:

a) приближенного вычисления значений функции f(x) для значений аргумента, в узлах интерполяции

b) приближенного вычисления значений функции f(x) для значений аргумента, отличных от узлов интерполяции

c) нахождение аналитического выражения функции проходящей через узлы интерполяции

d) нахождение аналитического выражения функции не проходящей через узлы интерполяции

e) нахождение аналитического выражения функции отстоящей от узлов интерполяции на заданном расстоянии

18. интерполяционная формула Лагранжа имеет вид:

a) где

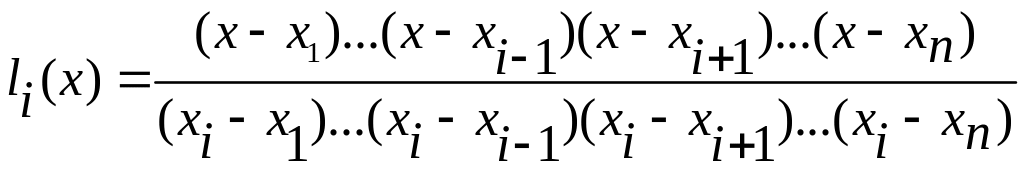
b) где

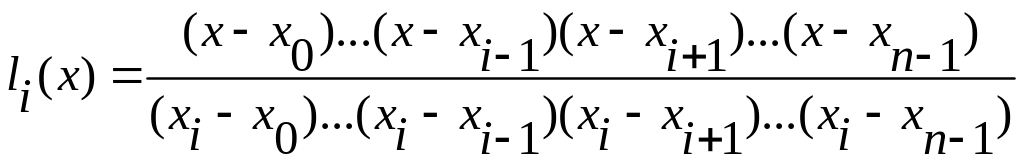
c) где

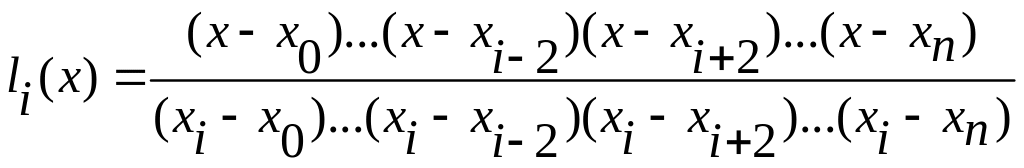
d) где

e) где

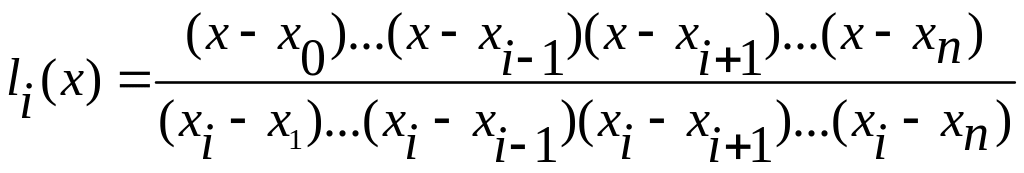
19. В интерполяционной формуле Лагранжа где - множитель Лагранжа. Важное свойство этих множителей:

a)

b)

c)

d)

e)

20. Конечная разность первого порядка – разность между значениями функции в данном узле и в предыдущем. Конечные разности высших порядков это-:

a) разность между значениями конечных разностей предыдущего порядка функции в данном узле и значениями в функции предыдущем

b) разность между значениями функции в данном узле и значениями конечных разностей предыдущего порядка функции предыдущем

c) разность между значениями функции в данном узле и значениями в функции в последнем узле

d) разность между значениями конечных разностей предыдущего порядка функции в данном узле и в предыдущем

e) разность между значениями функции в последнем узле и значениями в функции в данном узле

21. Какие три типа конечных разностей вы знаете?

a) нисходящие разности для интерполирования назад; восходящие разности для интерполяции вперед; центральные разности для построения центральных интерполяционных формул.

b) нисходящие разности для построения центральных интерполяционных формул; восходящие разности для интерполирования назад; центральные разности для интерполяции вперед

c) нисходящие разности для интерполяции вперед; восходящие разности для интерполирования назад; центральные разности для построения центральных интерполяционных формул.

d) нисходящие разности для интерполяции вперед; восходящие разности для построения центральных интерполяционных формул; центральные разности для интерполирования назад

e) нисходящие разности для интерполяционной формулой Лагранжа; восходящие разности для интерполирования назад; центральные разности для построения центральных интерполяционных формул.

22. Если точка х* находится в начале или конце таблицы, то не всегда возможно выбрать достаточное количество узлов слева и справа от х* для построения необходимых конечных разностей. В этом случае используются специальные формы интерполяционного многочлена, так называемого многочлена Ньютона. Для интерполирования в начале таблицы используется 1 интерполяционный многочлен Ньютона:

a)

b)

c)

d)

e)

23. Если точка х* находится в начале или конце таблицы, то не всегда возможно выбрать достаточное количество узлов слева и справа от х* для построения необходимых конечных разностей. В этом случае используются специальные формы интерполяционного многочлена, так называемого многочлена Ньютона. Для интерполирования в конце таблицы используется 2 интерполяционный многочлен Ньютона:

a)

b)

c)

d)

e)

24. Если требуется вычислить определенный интеграл на интервале [a;b] и задача не может быть решена аналитически, используют методы численного интегрирования. При этом подынтегральную функцию аппроксимируют какой-либо более простой функцией, а в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени получаем метод прямоугольников. Формулы левых и правых прямоугольников соответственно:

a) ,

b) ,

c) ,

d) ,

e) ,

25. Если требуется вычислить определенный интеграл на интервале [a;b] и задача не может быть решена аналитически, используют методы численного интегрирования. При этом подынтегральную функцию аппроксимируют какой-либо более простой функцией, а в качестве аппроксимирующей функции используют полином. В случае полинома первой степени получаем метод трапеций. Формула трапеций:

a) . При h=(b-a)/n  h ((y₀+y_n)/2+y₁+y₂+…+y_n-1).

b) . При h=(b-a)/n  h ((y₀ - y_n)/2+y₁+y₂+…+y_n-1).

c) . При h=(b-a)/n  h ((y₀+y_n)/2+y₁+y₂+…+y_n-1).

d) . При h=(b-a)/n  h ((y₀ - y_n)/2+y₁+y₂+…+y_n-1).

e) . При h=(b-a)/n  h ((y₀+y_n)/2+y₁-y₂-…-y_n-1).

26. Если требуется вычислить определенный интеграл на интервале [a;b] и задача не может быть решена аналитически, используют методы численного интегрирования. При этом подынтегральную функцию аппроксимируют какой-либо более простой функцией, а в качестве аппроксимирующей функции используют полином. В случае полинома второй степени получаем метод Симпсона, более точный результат можно получить, если заменить данную кривую параболой, проходящей через три точки. Формула Симпсона:

a) при n=2  (y₀ - 4y₂+y₄); при n=4  (y₀ - 4y₁+2y₂+4y₃+y₄)

b) при n=2  (y₀ - 4y₂+y₄); при n=4  (y₀ - 4y₁+2y₂ - 4y₃+y₄)

c) при n=2  (y₀+4y₂ - y₄); при n=4  (y₀+4y₁ - 2y₂+4y₃+y₄)

d) при n=2  (y₀+4y₂ - y₄); при n=4  (y₀+4y₁ - 2y₂+4y₃ - y₄)

e) при n=2  (y₀+4y₂+y₄); при n=4  (y₀+4y₁+2y₂+4y₃+y₄)

27. Квадратурные формулы Ньютона-Котеса для вычисления определенного интеграла =(b - a) . Частными случаями этих формул являются методы (укажите лишнее):

a) при n=2 метод Симпсона

b) при n=1 метод трапеций

c) при n=3 метод Ньютона или правило трех восьмых.

d) при n=4 метод Ньютона-Симпсона

e) при n=0 метод прямоугольников

28. При нахождении значения производных различных порядков функции f , заданной в виде таблицы или сложного аналитического выражения применяются методы численного дифференцирования. Простейшие выражения получаются в результате дифференцирования интерполяционных формул, например первой интерполяционной формулы Ньютона. Например, производная первого порядка вычисляется по формуле:

a)

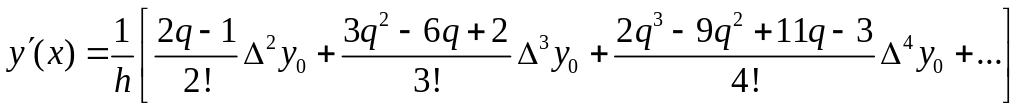
b)

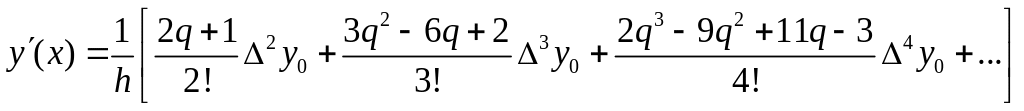
c)

d)

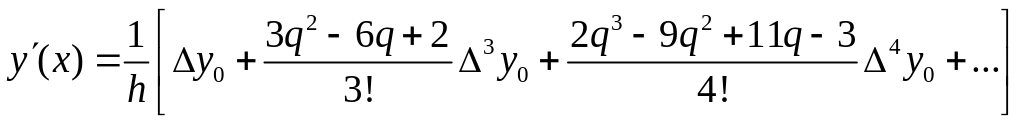
e)

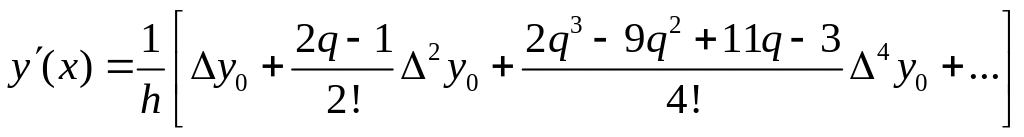
29. Уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называется:

a) интегральным уравнением

b) производным уравнением

c) линейным уравнением

d) нелинейным уравнением

e) дифференциальным уравнением

30. Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то дифференциальное уравнение называется:

a) сложным дифференциальным уравнением

b) обыкновенным интегральным уравнением

c) обыкновенным дифференциальным уравнением

d) обыкновенным производным уравнением

e) сложным производным уравнением

31. Если левая часть уравнения является многочленом по отношению к производной от неизвестной функции, то степень этого многочлена называется:

a) степенью производного уравнения

b) степенью дифференциального уравнения

c) показателем дифференциального уравнения

d) показателем производного уравнения

e) указателем дифференциального уравнения

32. Одним из методов решения обыкновенных дифференциальных уравнений является метод Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы:

a) аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала.

b) интерполируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала.

c) аппроксимируем решение (интегральную кривую) отрезком хорды, проведенной к графику решения в начале и конце интервала.

d) аппроксимируем решение (интегральную кривую) отрезком хорды, проведенной к графику решения в начале и середине интервала.

e) аппроксимируем решение (интегральную кривую) отрезком хорды, проведенной к графику решения в середине и конце интервала.

33. Одним из способов решения обыкновенных дифференциальных уравнений является метод Рунге-Кутта четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутта следующие , , , , . Тогда:

a)

b)

c)

d)

e)

34. Решение задачи линейного программирования состоит:

a) в нахождении допустимого решения (или плана)

b) в нахождении целевой функции

c) в нахождении оптимального плана

d) в нахождении канонической задачи линейного программирования

e) в определении ограничений задачи

35. План, при котором целевая функция задачи линейного программирования принимает свое максимальное (минимальное) значение, называется:

a) допустимым

b) не допустимым

c) не оптимальным

d) целевым

e) оптимальным

36. Совокупность чисел X = (x₁, x₂,…, x_n), удовлетворяющих ограничениям задачи линейного программирования, называется:

a) допустимым решением (или планом)

b) не допустимым решением

c) оптимальным

d) целевым планом

e) Симплекс решением

37. Симплексный метод решения задачи линейного программирования основан на:

a) переходе от одного не опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план обнуляется).

b) переходе от одного не опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является вырожденным).

c) переходе от одного опорного плана к другому, при котором значение целевой функции возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным).

d) переходе от одного опорного плана к другому, при котором значение целевой функции становится равным нулю (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является вырожденным).

e) переходе от одного не опорного плана к другому, при котором значение целевой функции становится равным нулю (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является вырожденным).

38. Метод решения транспортной задачи, когда на каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них мини­мальными тарифами называется

a) метод минимального элемента

b) методе се­веро-западного угла

c) метод потенциалов

d) метод аппроксимации Фогеля

e) метод дифференциальных рент

39. Метод решения транспортной задачи, когда заполнение клеток идет как бы по диагонали таблицы называется

a) метод потенциалов

b) метод аппроксимации Фогеля

c) методе се­веро-западного угла

d) метод минимального элемента

e) метод дифференциальных рент

40. Метод решения транспортной задачи, когда на каждом шаге следует выбирать какую-нибудь клетку, отвечающую мини­мальному тарифу называется

a) метод аппроксимации Фогеля

b) метод дифференциальных рент

c) метод минимального элемента

d) метод потенциалов

e) методе се­веро-западного угла

№	Ответ	№	Ответ	№	Ответ	№	Ответ	№	Ответ	№	Ответ
1	A	8	B	15	E	22	D	29	E	36	A
2	C	9	C	16	C	23	B	30	C	37	C
3	E	10	A	17	B	24	A	31	B	38	D
4	B	11	B	18	D	25	C	32	A	39	C
5	D	12	E	19	A	26	E	33	C	40	C
6	D	13	D	20	D	27	D	34	C
7	B	14	A	21	C	28	C	35	E