1.2 Спрямление кривых при помощи функциональных сеток

Если некоторую зависимость y = f (x) изображать графически, применяя сначала равномерную сетку, а затем различные функциональные сетки, то, очевидно, форма кривой во всех случаях будет неодинаковой. Этим пользуются на практике, выбирая функциональ­ные шкалы на осях координат такого вида, при котором данная кривая получает возможно более простую фор­му, например, преобразуется в прямую линию.

Так, логарифмическая [lg(y) = f(lg(x))] и полулога­рифмическая [y = f(lg(x))] сетки дают возможность пре­образовывать ряд кривых в прямые линии или, как говорят, спрямлять кривые.

В таблице 1 приведены типы функциональных сеток для прямолинейного преобразования некоторых видов уравнении.

Таблица 1 – Типы функциональных сеток для прямолинейного преобразования

Уравнение	Функциональные сетки для прямолиней­ного преобразования

1.3Представление данных с помощью уравнений

На основании опытных данных, состоящих из ряда соответствующих значений двух каких-либо величин, может быть подобрано алгебраическое выражение, ко­торое в пределах опыта с достаточной точностью опре­деляет зависимость между этими величинами — эмпи­рическая формула. Значения постоянных коэффициен­тов в этой формуле вычисляются на основании резуль­татов измерений.

1.4 Графический метод

Построив при помощи функциональной сетки пря­мую , где, например, Y = lg y, X = lg x , вычисляют постоянные коэффициенты а и b уравнения этой прямой, так как значение а определяется ординатой точки пересечения прямой с осью Y, а значение b соответствует тангенсу угла, который образует прямая с положительным направлением оси X.

Определив значения коэффициентов а и b, получа­ют эмпирическую формулу, устанавливающую зависи­мость между величинами X и Y. На основании этой формулы можно затем найти эмпирическую формулу, устанавливающую зависимость между величинами х и у.

1.5 Методика выполнения расчетов

На основании варианта задания, приведенного в Приложении А, установить закон роста окисной пленки для заданного металла.

1 Используя справочные данные Приложения Б рассчитать объёмное отношение для оксида металла:

,

где V_ок – объем 1 моля оксида, см³; V_Ме – объем металла, израсходованного на образо­вание 1 моль оксида, см³; М – молекулярная масса оксида, г; А – атомная масса металла, г; ρ_ок – плотность оксида, г/см³; ρ_Ме – плотность металла, г/см³; m – число атомов металла в молекуле оксида.

Отметить, отвечает ли оксид заданного металла условию сплошности

2 По исходным данными, определить площадь поверхности исследуемого образца – S, м².

3 Рассчитать удельное увеличение массы образца

, г/м²

где m –масса образца через время коррозии τ, г; m₀ – начальная масса образца, г; S – площадь поверхности образца, м².

4 Результаты расчетов свести в таблицу 2.

Таблица 2 – Результаты расчетов

№ опыта	Время коррозии τ, ч	Масса образца за время коррозии m, г	Удельное увеличение массы образца , г/м2

5 Определить положительные и отрицательные показатели изменения массы и :

г/(м²·ч);

г/(м²·ч)

где n — валентность металла, А – атомная масса металла.

6 Определить глубинные показатели коррозии П:

, мм/год

7 На основании полученных данных построить график зависимости Δm = f (τ)

8 Спрямить график при помощи одной из функциональных сеток, найти постоянные коэффициенты данного закона роста оксидной плёнки.

8.1 Например, если закон окисления линейный , то для нахождения константы k₁ строят график Δm = f (τ), представляющий собой прямую линию, тангенс угла наклона которой равен k₁.

8.2 В случае степенного закона , для нахождения показателя степени n и константы кривую спрямляют, построив график в координатах lgΔm = f (lgτ), который должен дать прямую. Уравнение этой прямой имеет вид: , где , - отрезок, отсекаемый на оси ординат при (см. рисунок 1.2).

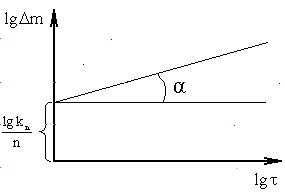
Рисунок 1.2 – Графическая зависимости lgΔm = f (lgτ)

8.3 В случае логарифмического закона роста оксидной пленки: , для нахождения констант k и const строят график Δm = f (lgτ), где k = tgα и const - это отрезок, отсекаемый на оси ординат при (см. рисунок 1.3).

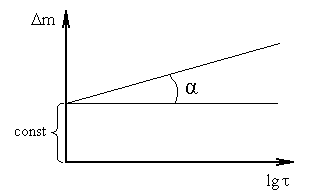
Рисунок 1.3 – Графическая зависимость Δm = f (lgτ)

8.4 В случае, если окисление металла идет по квадратному уравнению: , для нахождения k₁ и k₂ уравнение преобразуют к виду: , строят график в координатах , который должен дать прямую линию, где , - отрезок, отсекаемый на оси ординат при Δm = 0.

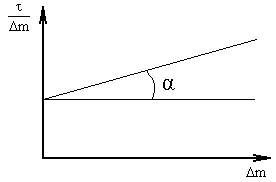
Рисунок 1.4 – Графическая зависимость

9 После построения графиков и графического нахождения коэффициентов, устанавить закон окисления данного металла, в данных условиях (не в общем виде, как дано в условии, а с найденными коэффициентами, например, )

10 Оценить адекватность установленного закона окисления металла. Для этого вычислить погрешность проведенных расчетов.

Расчета погрешности ведется по формуле

,

где m_оп - масса образца за время коррозии τ, (из условия);

m_расч - масса образца за время коррозии τ, рассчитанная из теоретически установленного закона.

Δ - погрешность в абсолютном значении.

По найденной теоретической зависимости рассчитать удельное изменение массы Δm_расч, затем – m_расч.

Например, если установлен закон , то Δm_расч1= , а и т.д. Погрешность адекватности найденной теоретической зависимости не должна превышать ∆ = ±0,005г.

11 В конце работы сделать вывод, о выполнении условия сплошности оксидной пленки, механизме контроля процесса окисления металла и найденной эмпирической зависимости Δm = f (τ).