3 Нелінійні структури даних

3.1 Мета роботи – Ознайомлення з базовими нелінійними структурами даних, класичними моделями і методами розв’язання завдань на їхній основі.

3.2 Методичні вказівки з організації самостійної роботи студентів

До найпоширеніших нелінійних структур даних відносяться дерева, графи й хеш-таблиці.

Деревом називається сукупність однотипних елементів (вузлів), що утворюють ієрархічну структуру на базі відношення батько-нащадки. Прикладом дерева є багаторівневий зміст книги. Коренем дерева називається єдиний вузол дерева, що не має над собою батька. Дерево називається бінарним (двійковим), якщо будь-який його елемент має не більше двох нащадків. Приклад дерева наведений на рис. 3.1. Це дерево є бінарним.

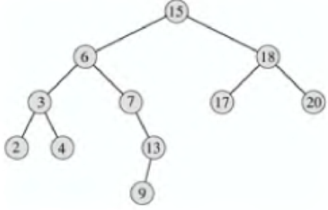
Рисунок 3.1 - Бінарне дерево

Ієрархічна структура, утворена одним з нащадків кореневого вузла й всіма його піделементами також є деревом. Це дає рекурентне визначення дерева:

• один вузол є деревом. Цей вузол називається коренем дерева;

• нехай n – це вузол, а T₁,T₂, … T_k – дерева з корінням n₁,n₂,…,n_k відповідно. Можна побудувати нове дерево, роблячи n батьком вузлів n₁,n₂,…,n_k... У цьому дереві n буде коренем, а T₁,T₂,…, T_k – піддеревами цього кореня. Вузли n₁,n₂,…,n_k – називаються синами вузла n.

Існує кілька способів обходу дерева, три найбільше часто використовувані з них – це обхід у прямому, зворотному (у глибину) і симетричному порядку.

Нехай функції Traverse_X(root) здійснюють обхід дерева з коренем root. Визначимо також загальні абстрактні функції для роботи з деревом:

Data(root) – повертає корисні дані, збережені у вузлі root;

GetChildren(root) – одержує колекцію дочірніх елементів вузла root;

GetNextChild(root) – одержує чергового нащадка з колекції дочірніх елементів вузла root;

Parent(root) – одержує батьківський вузол для root;

GetLeftChild(root) - одержує самого лівого нащадка вузла root;

GetRightChild(root) - одержує самого правого нащадка вузла root.

Тоді прямий обхід дерева можна виразити як:

Traverse_Straight(root)

begin

Process(Data(root))

foreach son in GetChildren(root)

Traverse_Straight(GetNextChild(root))

end

Зворотний обхід (обхід у глибину):

Traverse_Backward(root)

begin

foreach son in GetChildren(root)

Traverse_Backward(GetNextChild(root))

Process(Data(root))

end

Симетричний обхід застосовується в основному для бінарного дерева:

Traverse_Symmetric(root)

begin

Traverse_Symmetric(GetLeftChild(root))

Process(Data(root))

Traverse_Symmetric(GetRightChild(root))

end

Також іноді використовується обхід вершин дерева завширшки, тобто по рівнях глибини. Елементи однакової глибини обходять зліва направо.

Сфера застосування дерев дуже велика. Прикладами таких застосувань є: реалізація АТД множина на бінарному дереві пошуку [1 c.146-151], реалізація АТД черга із пріоритетами на частково впорядкованому дереві [1 c.129-137], реалізація перебірних алгоритмів на деревах рішень [1 c.291 – 301, 3 розділ 5.-7.], реалізація словників на навантажених деревах [1 c.152-158], проведення обчислень на позначених деревах [1 с. 79-83] та ін.

Способи реалізації дерев. Найпоширенішими є два варіанти реалізації дерев: 1) на динамічній пам'яті; 2) на масиві.

При реалізації дерева на динамічній пам'яті кожен вузол дерева представляється у вигляді структури

const MAX_CHILD_COUNT = 10;

struct TTreeNode{

int data; // корисні дані довільного типу

TTreeNode * children[MAX_CHILD_COUNT]; // масив адрес нащадків

TTreeNode *Parent; //адреса батьківського вузла

};

Якщо кількість нащадків заздалегідь невідома й може бути змінною у різних вузлів дерева, то для економії пам'яті можна зберігати нащадків в однозв'язному або двузв'язному списках (рис 2.2).

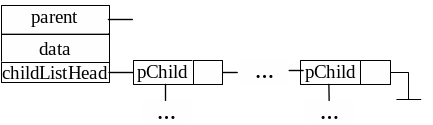
Рисунок 2.2 - Модель реалізації вузла дерева зі списком нащадків. ChildListHead - адреса початку списку нащадків

Також іноді використовується модель подання кожного вузла дерева як структури з посиланнями на батька, самого лівого нащадка й правого брата.

Для бінарного дерева часто використовують спрощену структуру:

struct TBinaryTreeNode{

int data; // корисні дані довільного типу

TBinaryTreeNode * Left; // адреса лівого нащадка

TBinaryTreeNode * Right; // адреса правого нащадка

};

Адресу батьківського вузла можна не зберігати, якщо алгоритми обробки дерева побудовані без повернень із нижніх рівнів на верхні, або повернення реалізовані за допомогою додаткових структур даних, таких як стеки або черги.

Можлива також реалізація дерев на масиві, де вони розташовуються по рівнях глибини. У цьому варіанті реалізації починаючи з індексу 0 масиву розташовується корінь потім всі його безпосередні нащадки, потім безпосередні нащадки першого нащадка кореня, всі безпосередні нащадки другого нащадка кореня й т.ін. У такому варіанті j-й нащадок вузла з індексом i у масиві для дерева із числом нащадків у кожного вузла m буде розташовуватися за індексом m*i+j. Можна вивести також зворотну формулу для обчислення індексу батька за індексом нащадка.

3.3 Варіанти індивідуальних завдань

1. Реалізувати АТД «черга із пріоритетами» на основі АТД «частково впорядковане дерево» [1 c.129-137]. На основі черги промоделювати перегони машин. Модель може виглядати наступним чином: задана дистанція довжиною M метрів; кожна машина характеризується маркою (рядок символів), поточною координатою на прямолінійній трасі та поточною швидкістю (ціле число); у нульовий час відліку всі машини стоять на старті (мають нульову координату) та наділені кожна своєю початковою швидкістю; якщо розмістити всі машини у чергу з пріоритетами, вважаючи за пріоритет швидкість машини, то на початку черги опиниться машина з найбільшою швидкістю (пріоритетом); вилучаємо її з черги та обробляємо – зсуваємо на один метр вперед; якщо машина досягла фінішу фіксуємо зайняте нею місце у перегонах, інакше – змінюємо її швидкість випадковим чином та знову додаємо до черги; обробляємо елемент з початку черги доти, доки черга не спорожниться (всі машини не дойдуть до фініша). У якості результата виводити розташування всіх машин на кожній ітерації обробки елемента черги та ітогову таблицю гонок (машина, зайняте нею у перегонах місце).

2. Реалізувати АТД «множина» на двійковому дереві пошуку [1 c.146-151]. Операції: додавання елемента у множину, вилучення елементу, пошук елементу, об’єднання, перетин та різниця множин. Продемонструвати роботу виконання всіх реалізованих над множиною операцій.

3. Реалізувати тлумачний словник на основі навантаженого дерева (операції вставки, вилучення, пошуку слова, виводити словник на екран за абеткою). [1 c.152-158]

4. Реалізувати гру хрестики-нулики людини з комп'ютером. Комп'ютер ухвалює рішення щодо ходу на підставі аналізу дерева рішень. [1. c.291 - 301, 4. розділ 5.-7.]

5. Реалізувати гру «Балда» людина-комп'ютер на основі словника на навантаженому дереві: кожен гравець по черзі приписує букву до слова, програє той, хто останній поставить букву (коли слово закінчується). [1 c.85-90, с.152-158]

6. Реалізувати АТД «множина» на 2-3 дереві [1 с.158-167]. Операції: додавання елемента у множину, вилучення елементу, пошук елементу, об’єднання, перетин та різниця множин.

3.4 Контрольні питання й завдання

1. Назвіть відомі Вам нелінійні структури даних.

2. Які види дерев Вам відомі? Які властивості виконуються для них?

3. Які існують алгоритми обходу дерев? Приведіть практичний приклад їхнього використання.

4. Які є способи внутрішньої організації АТД множина?

5. Які є переваги у 2-3 дерева перед двійковим деревом пошуку для організації ефективного внутрішнього подання множин?