Тема 4. Епюр 2. Розгортка піраміди

Розгорнути поверхню – це значить, сумістити її всіма точками з площиною [1 с. 42-43]. Для того щоб побудувати розгортку багатогранника необхідно знати натуральні розміри (дійсну величину) ліній, що визначають її контур.

Побудувати розгортку піраміди SABC (рис. 15).

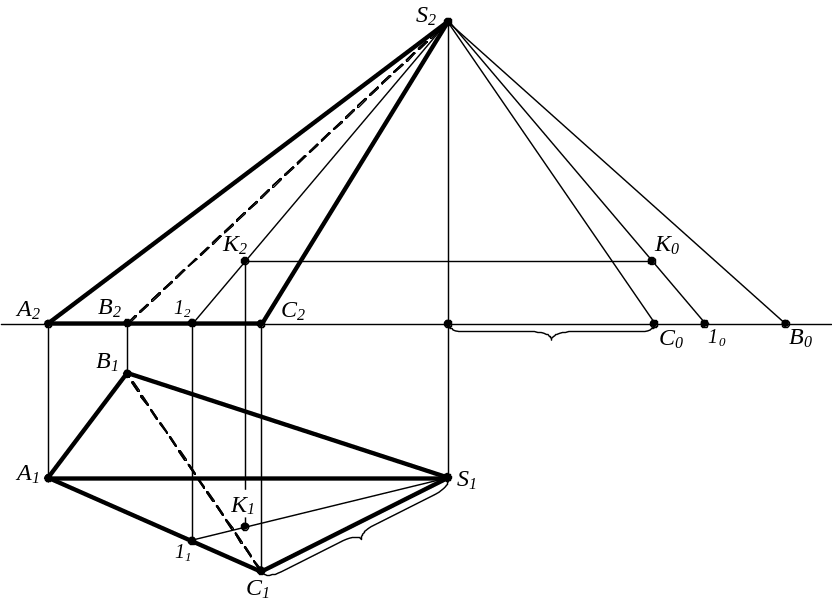
Рис. 15

У даному випадку основа піраміди (рис. 15) ∆ABC лежить у горизонтальній площині рівня, отже, проецюється на горизонтальну площину проекцій (П₁) без спотворення. Ребро AS паралельно площини П₂, тому A₂S₂ – натуральний розмір цього відрізка. Для розв'язання поставленої задачі необхідно визначити натуральні розміри ребер BS і CS. Тут зручно використовувати засіб прямокутного трикутника. Натуральні розміри ребер піраміди являють собою гіпотенузи прямокутних трикутників, у яких один спільний катет дорівнює різниці координат "z" вершини піраміди S і кінців ребер – точок В і С, а другі катети рівні горизонтальним проекціям відповідних ребер.

Щоб побудувати на розгортці точку (рис. 16), що належить поверхні багатогранника, необхідно "прив'язати" її до поверхні за допомогою якоїсь лінії, що належить цій поверхні, і перенести цю лінію на розгортку з урахуванням її натурального розміру (рис. 15), що дозволяє виміряти відстань до шуканої точки від якоїсь іншої вже відомої точки.

Рис. 16

Питання та задачі для самоконтролю

1. Що таке "комплексне креслення"?

2. Які координати точки визначають її – горизонтальну проекцію;

фронтальну проекцію;

профільну проекцію?

3. Якщо А(20,15,40), В(20,25,25) – яка з цих точок простору розташована вище;яка з цих точок розташована ближче до спостерігача?

4. Які способи визначення дійсної величини відрізку ви знаєте?

5. Що означає "розгорнути" поверхню?

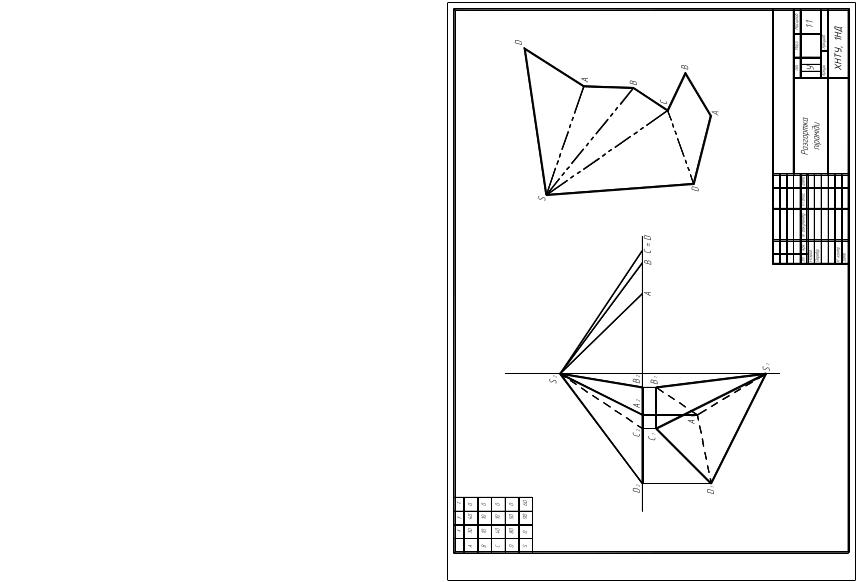
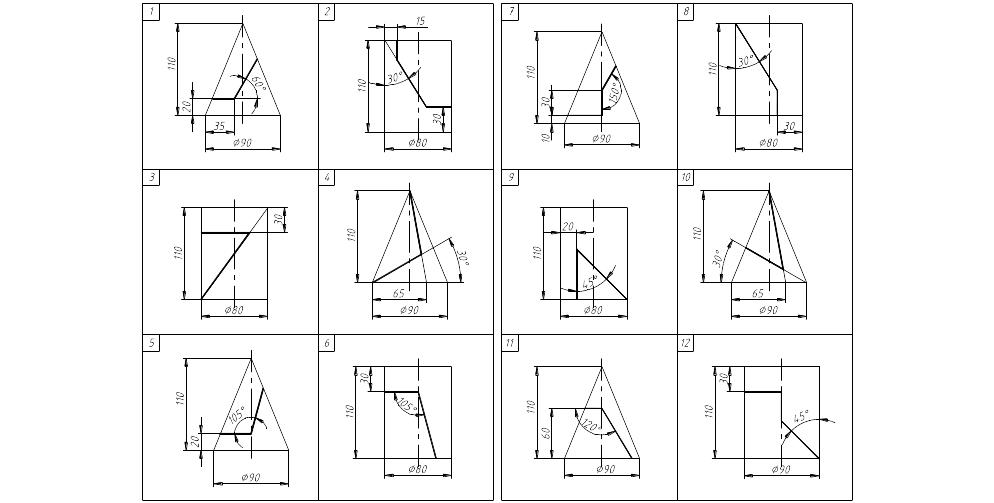
Завдання по темі 4 – "Епюр № 2. Розгортка піраміди"

Виконати креслення на листі креслярського паперу формату А3.

1. По заданим координатам вершини S і вершин основи A, B, C, D (табл. 2) побудувати комплексне креслення піраміди (з урахуванням видимості).

2. Побудувати розгортку піраміди.

Приклад виконання див. с. 45.

Варіанти завдання див. с. 46, табл. 3.

Таблиця 3

Тема 5. Епюр 2. Перетин поверхні обертання площиною окремого положення

Поверхні обертання утворюються обертанням якийсь утворюючої (прямої або кривої) навколо нерухомої осі. Оскільки при утворенні поверхні обертання кожна точка утворюючої описує коло у площині, перпендикулярної осі обертання, то розріз поверхні обертання площиною, перпендикулярною до осі обертання – завжди коло. Якщо січна площина нахилена до осі обертання поверхні переріз може являти собою еліпс, або іншу плоску криву, у конічних перерізах це може бути парабола, гіпербола, та ін. [2 с. 108-111, 10 с. 39-40].

Якщо січні площини є площинами окремого положення (проецюючі площини), то одна проекція перерізу зображується прямою лінією (на рис. – фронтальна проекція перетину є прямою лінією, тому що січні площини фронтально-проецюючі). Вибираючи на цій проекції точки (1, 2, 3, 4, 5), що належать січним площинам, можна побудувати їх відсутні проекції, використовуючи умову приналежності цих точок до заданої поверхні. Для цього використовують лінії, що належать заданій поверхні і проходять через обрані точки. Переріз січною площиною якій належать точки 4 та 5 являє собою трикутник, бо січна площина проходить через вершину конуса. Переріз січною площиною Переріз січною площиною якій належать точки 1, 2, 3, 4 являє собою еліпс. Для побудови перетину еліпс (або інші лекальні криві) найчастіше використовують паралелі поверхонь обертання, тобто окружності – наслідок перетинання поверхні обертання площиною, перпендикулярної до її осі. Як відомо, радіус паралелі обумовлюється відстанню від осі поверхні до перетину площини паралелі з нарисом.

Насамперед, аналізуючи положення січної площини стосовно осі поверхні обертання, думкою обумовлюють форму перетину [10 с. 39-40]. У даному прикладі (рис. 17) в перетині поверхні еліпс.

Побудова фігури перетину починається з визначення опорних точок:

Найбільш високої і низької, самої ближньої і найдальшої, границь видимості та ін.

На рис. точка 5 – верхня, точка 1 – нижня, точка 4 – належить лінії перетину січних площин. У тих місцях, де опорні точки розташовані нерівномірно чи між ними занадто великі відстані, що не дозволяє досить точно побудувати контур перетину, вибирають довільно розташовані проміжні точки – 2 і 3.

Рис. 17

Дійсний вид перерізу визначають за допомогою заміни площин проекцій. Нова площина проекцій повинна бути паралельна січної площини, а отже, нова вісь х₁ паралельна прямої – проекції цієї січної площини.

Нові лінії зв'язку перпендикулярні цієї осі. При цьому координати на цих лініях зв'язку зручно відкладати симетрично від осі х₁ , що повинні бути попередньо обмірювані від осі симетрії перетину з замінної проекції.

Питання та задачі для самоконтролю

1. Яка поверхня називається поверхнею обертання?

2. Назвіть основну властивість поверхні обертання?

3. Яку геометричну форму можуть мати перерізи циліндру обертання? конуса? кулі?

4. Які точки перерізу відносяться до "опорних" точок?

5. Який метод побудови перерізу поверхонь обертання вам відомий?

6. Яким методом можливо визначити правдивий вид перерізу?

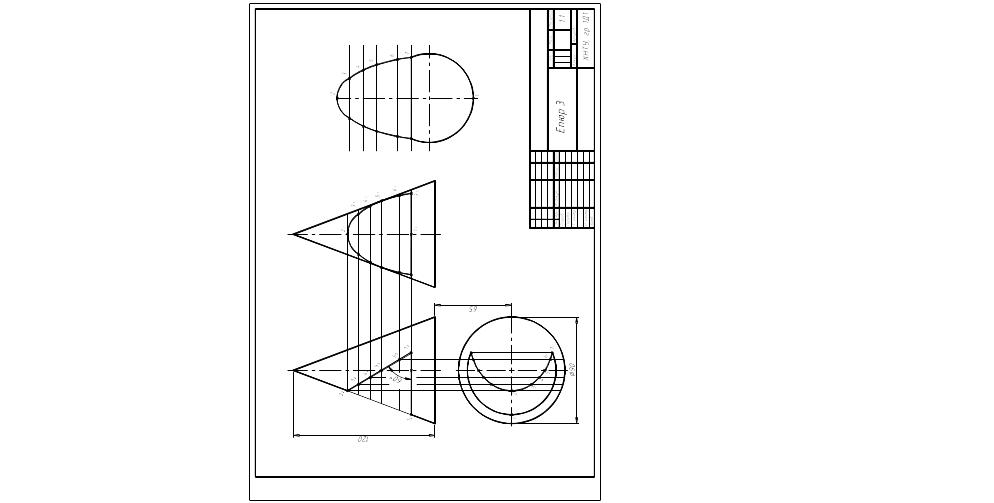
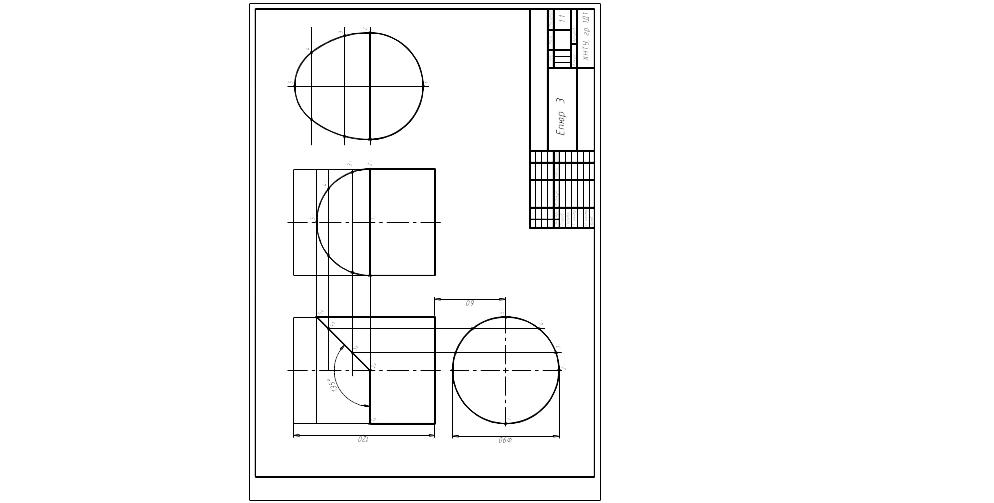
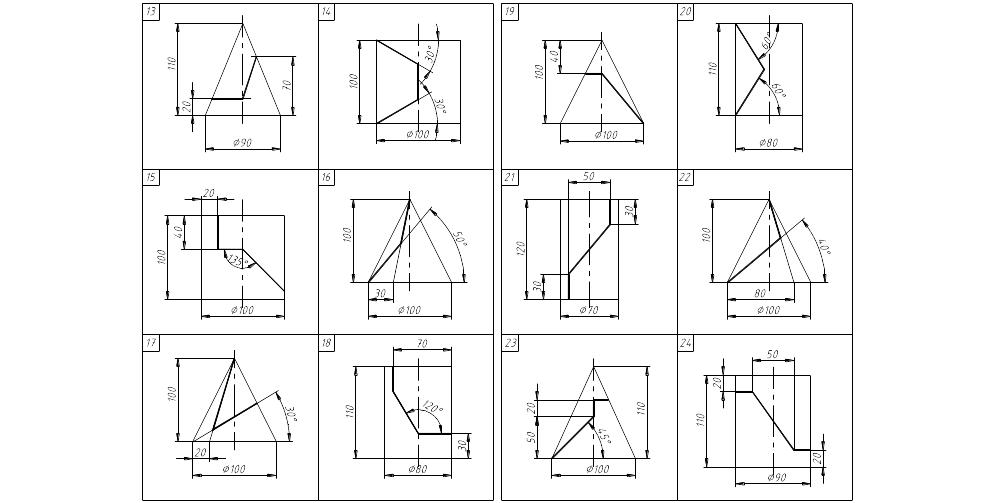
Завдання по темі 5 – "Епюр № 2. Перетин поверхні обертання площиною окремого положення "

Виконати креслення на листі креслярського паперу формату А3.

Приклад виконання див. с. 50, 51.

Варіанти завдання див. с. 52-55 .

Література

1. Михайленко В.Є., Інженерна графіка: Підручник для студ. вищих закл. освіти/ В.Є. Михайленко, В.В. Ванін В.В., С.М. Ковальов – К. Каравела, 2004. – 288 с.

2. Антонович Є.А. Креслення: навч. посібник/ Є.А. Антонович, Я.В. Василишин, В.А. Шпільчак; за ред. проф. Антоновича. – Львів: Світ, 2006. – 512 с., іл.

3. Верхола А.П.Інженерна графіка: креслення, комп¢ютерна графіка: Навчальний посібник/ А.П. Верхола,Б.Д. КоваленкоК. , В.М. Богданов – Каравела, 2005. – 304 с.

4. Бубенников А.В. Начертательная геометрия/ А.В. Бубенников, М.Я. Громов М. ВШ, 1973. – 421 с.

5. Чекмарев А.А. Инженерная графика/ А.А. Чекмарев – М. ВШ, 1988. – 335с.

6. Четверухин Н.Ф. Курс начертательной геометрии/ Н.Ф. Четверухин и др. – М. ВШ, 1968. – 435 с.

7. Федоренко В.А. Справочник по машиностроительному черчению/ В.А. Федоренко, А.К. Шошин – Л., Машиностроение, 2003.

8. ЕСКД – Общие правила выполнения чертежей. Москва. Издательство стандартов, 1988. – 240 с.

9. Левицкий В.С. Машиностроительное черчение: Учебник для студентов высших технических учебных заведений/ В.С. Левицкий – М. ВШ, 1988 – 351 с.

10. Ісаєва Т.М., Нарисна геометрія (конспект лекцій)/ Т.М. Ісаєва, В.О. Ткач – Херсон. ХНТУ, 2007. – 62 с.

11. Богданов В.Н. Справочное руководство по черчению/ В.Н. Богданов – М. Машиностроение, 1989. – 864 с.

Ткач Віра Олексіївна

Войтович Ольга Андріанівна

Методичні рекомендації та індивідуальні завдання для практичних занять і самостійної роботи студентів з дисципліни "Нарисна геометрія"

для напряму: 6.020207 – "Дизайн"

44