3. Многошаговые процессы управления

Среди разнообразных задач управления значи­тельное место занимают задачи, в которых объект управ­ления находится в состоянии непрерывного изменения под воздействием различных внешних и вну­тренних факторов. Задачи управления такими объектами относятся к классу динамических задач управления.

Объект называется управляемым, если среди дейст­вующих на него разнообразных факторов имеются такие, распоряжаясь которыми, можно изменять характер его движения. Как уже указывалось, такие целенаправлен­ные воздействия называются управлениями и обозна­чаются u(t).

Оценить, насколько при том или ином способе управ­ления достигаются поставленные цели, можно, как и раньше, путем введения целевой функции типа, которую в данном случае удобно записать в виде

Если целевая функция имеет физический смысл потерь, то она определяет суммарные по­тери за весь процесс управления.

В целом ряде случаев характер движения объ­екта в процессе управления не представляет существен­ного интереса, а важным является только состояние, которое примет объект в момент окончания процесса управления. Такие задачи по­лучили название задач управления конечным состоя­нием.

Обозначим через х(Т) состояние объекта в конечный момент времени. Целевая функция в данной задаче бу­дет иметь вид:

Поскольку х(Т) зависит от характера примененного управления u(t), то и значение q также будет зависеть от примененного управления. Поэтому задачу выбора оптимального управления можно сформулировать для этого случая следующим образом: из пространства до­пустимых управлений U выбрать такое управление u*(t), которое для объекта минимизирует целевую функцию при ограничениях на используемые ре­сурсы.

Нахождение оптимального управления в дина­мических системах во многих случаях существенно об­легчается, если процесс управления удается разбить естественным или искусственным путем на отдельные шаги или этапы.

Для того чтобы вести рассмотрение в общем виде, будем считать, что состояние объекта описывается мно­гомерной переменной

Предположим, что динамический процесс х( t) на интервале от 0 до t^ может быть естественным или искусственным образом представлен как многошаговый, и найдем подходящий способ описания такого процесса. Для того чтобы получить многошаговый процесс, интер­вал от 0 до t^ должен быть разбит на п последовательных шагов, длительности которых примем равными как показано на рис. 2. Обозначим через моменты окончания k-гo шага так, что а через x_k состояние объекта в момент t_k:

x_k = x(c, t_k), где с=х(0).

Состояние

Рис. 2. Разбиение интервала на п шагов.

Это выражение мож­но представить в виде

Оно представляет собой состояние объекта , как результат преобразования состояния x_k на (k+1)-м шаге.

Введем в рассмотрение оператор Т, который будет означать преобразование состояния процесса за один шаг:

Тогда можно записать

Полагая k = 0, 1,...,п-1, можем описать весь дина­мический процесс в виде последовательности преобра­зований

Динамический процесс, описываемый рассмотренным преобразо­ванием, является неуправляемым. Для получения управляемого многошагового процесса необходимо иметь возможность на каждом шаге осуществлять не одно пре­образование Т(х_к), а одно из множества преобразова­ний T₁(x_k),...,T_r(x_k).

Удобно считать, что конкретный вид преобразования будет зависеть от параметра u_k, который на k-м шаге может принимать одно из множества значений U_k. Па­раметр u_k будем называть управлением, а множество U_k — пространством допустимых управлений на k-м ша­ге. Преобразование, осуществляемое на k-м шаге, теперь можно записать в виде

Если в соотношении положить последователь­но k=0, 1,...,n-1 и учесть начальное состояние х₀, то получим описание всего управляемого многошагового процесса:

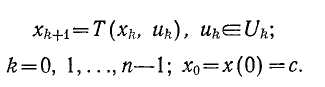
Пример. Предположим, что переменная состояния является двумерной величиной х=(х⁽¹⁾,x⁽²⁾), которая может принимать значения, определяемые геометрически узлами сетки, изображенной на рис. 3, а. Переход от одного узла сетки к следующему произво­дится путем использования на каждом шаге одного из двух возможных управлений: u_k=0 – движение по горизонтали и u_k=1 – движение по вертикали. Следовательно, пространство допустимых управлений одинаково для любого шага и равно U_k = {0,1}, k=0,1, ...,п-1.

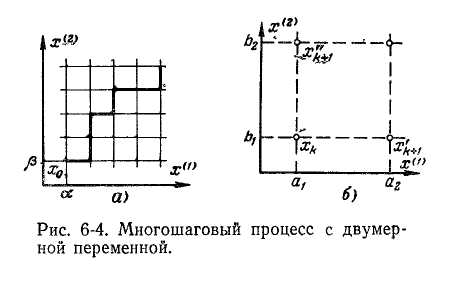
Рис. 3. Многошаговый процесс с двумерной переменной

Рассмотрим одну из клеток данной сетки, показанную на рис. 3, б, в нижнем левом узле которой система оказалась после k-го шага, так что Значение зависит от примененного управления. Как видно из рис. 4 б имеют место следующие соотношения:

Конкретную траекторию движения системы можно описать, указав начальное состояние х₀ и последовательность примененных управлений. Так, отмеченная жирной линией траектория на рис. 3, а получается при использовании управления и= (01101001) и при начальных условиях

Качество управления опреде­ляется значением целевой функции q, численное значение которой можно рассматривать как потери, которые мы несем, применяя то или иное управление. Потери за один шаг будут зависеть от состояния процесса в начале шага и примененного на этом шаге управления, т. е.

За критерий качества управления можно принять полные потери за все п шагов процесса и представить критерий качества управления n-шагового процесса в виде

Здесь через и обозначена последовательность управ­лений, т. е. упорядоченное множество вида

Если рассматривается многошаговый процесс управ­ления конечным значением, то потери будут зависеть лишь от состояния объекта управления в конце процес­са, которое в свою очередь зависит от начального состоя­ния и примененных на каждом шаге управлений:

q=q(x_n)=Q(x₀ , и).

Ве­личину q выражением будем назы­вать целевой функцией многошагового процесса управ­ления.

Задача нахождения оптимального управления при многошаговом процессе может быть сформулирована сле­дующим образом. Для динамической системы, найти такую последовательность (цепочку) управлений , которая обращает в минимум критерий качества управления. Помимо указанной задачи встречаются случаи, когда необходимо в единственной последовательности (цепочке) управления, найти такое управление, при котором критерий качества достигает экстремума. Решаются такие задачи методом перебора.

Рассмотрим некоторые примеры.

1. Задача о замене оборудования.

Требуется разработать политику относительно эксплуатации оборудования старше t лет при следующих условиях : стоимость произведенной за год продукции r(t), возраст которой t лет, и стоимость затрат u(t) на обслуживание этого оборудования приведены в табл.6. Стоимость нового оборудования р(t)=8 ед.

Таблица 6

Параметры t, r(t), u(t)	Значения параметров t, r(t), u(t)
t	0	1	2	3	4	5	6	7	8	9	10
r(t)	24	24	24	23	23	22	21	21	21	20	20
u(t)	13	14	15	15	17	17	17	18	19	19	20

В задаче замены устаревшего оборудования показатель эффективности на k-м шаге запишется в виде:

 r(t)-u(t) при сохранении оборудования,

Q_к (t) = 

 r(0)-u(0)-8 при замене оборудования,

где r(t) – стоимость продукции, произведенной за год на оборудовании, возраст которой t лет; u(t) – сметные затраты на обслуживание оборудования; s(t) - остаточная стоимость оборудования.

В рассматриваемой задаче за шаг берется один год эксплуатации оборудования, за состояние – срок эксплуатации, а за управление – сохранение или смена оборудования.