2.1. Линейное программирование

Допустим, дана система т линейно независимых уравнений с n неизвестными x₁,…, х_п, называемая системой ограниче­ний задачи линейного программирования:

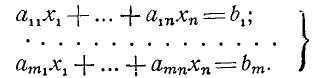
Характерной особенностью данной задачи является то, что число уравнений меньше числа неизвестных, т. е. m<n. Требуется найти неотрицательные значения пере­менных , которые удовлетворяют урав­нениям ограничения и обращают в минимум целевую функцию

Иногда в задаче линейного программирования все или некоторые из уравнений имеют вид не­равенств. Так, вместо уравнения

в систему может входить неравенства вида

или

От таких неравенств легко перейти к урав­нениям, вводя добавочную переменную х_n+j0 так, что­бы в зависимости от знака неравенства имело место одно из двух выражений

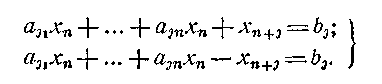
Поскольку число переменных п в этой системе больше числа уравнений т, то одно из возможных решений можно найти, если п—т каких-либо переменных положить равными нулю. Полученную при этом систему т уравнений с т неизвестными можно ре­шать обычными методами линейной алгебры. Правда, для того чтобы система т уравнений с т неизвестными имела решение, необходимо, чтобы определитель, составленный из коэффициентов при неизвестных, не обращался в нуль. Если это условие не выполняется, то можно приравнять нулю другие п—т переменных. Полученное при этом решение называется базисным решением.

Базисом называется любой набор т переменных, та­ких, что определитель, составленный из коэффициентов, при этих переменных не равен нулю. Эти т переменных называются базисными переменными (по отношению к данному базису). Остальные п—т переменных называются небазисными или свободными переменными В каж­дой конкретной системе уравнений может сущест­вовать несколько различных базисов с различными ба­зисными переменными.

Если положить все свободные переменные равными нулю и решить полученную систему т уравнений с т неизвестными, то получим базисное решение. Однако среди различных базисных решений будут такие, кото­рые дают отрицательные значения некоторых перемен­ных. Эти базисные решения противоречат условию зада­чи и являются недопустимыми.

Решение задачи линейного программирования симплекс-методом

Существо симплекс-метода состоит в следующем. Прежде всего, находится допустимое базис­ное решение. Его можно найти, приняв из числа п переменных какие-либо п—m переменных за свободные, приравняв их нулю и решив получившуюся систему уравнений. Если при этом некоторые из базисных переменных окажутся отрица­тельными, то нужно выбрать другие свободные перемен­ные, т е перейти к новому базису.

Каждое базисное реше­ние, проверяется, на достижение минимума целевой функции. Если минимум не достигут, то ищут новое допустимое базисное решение, но не любое, а такое, которое уменьшает зна­чение целевой функции. Затем процедура повторяется.

Решение линейной задачи симплекс-методом ведется в следующей последовательности.

1. Из вектора переменных размерностью n выбирают переменные, число которых равное числу уравнений ограничений m, их принимают за однозначно определенные (базисные) переменные. Остальные (n-m) переменных принимают за свободные и приравнивают их нулю.

2. Базисные переменные, исходя из уравнений ограничений, выражают через свободные переменные в виде линейной комбинации

.

После преобразования составляется каноническая форма записи модели, из которой определяются х_i. Эту запись иногда называют симплекс-планом или опорным планом. Модель записывается в виде следующей системы уравнений:

.

Для того чтобы проверить отвечает ли составленная система поставленной цели (определение оптимальных значений х_i), необходимо полученные значения базовых переменных подставить в целевую функцию

,

где - значение целевой функции, определяемое свободными членами , и проанализировать полученную целевую функцию. Если в целевой функции все коэффициенты , то опорный план оптимальный. Следовательно, оптимальное решение запишется в виде:

Если в целевой функции некоторые коэффициенты <0, то план не оптимален. Необходимо строить новый план. Для этого по симплекс-методу одну из свободных переменных (ту, у которой ) необходимо перевести в разряд базовых, а одну из базисных переменных перевести в разряд свободных и составить новый опорный план. Далее процедуру повторяют. Смену переменных выполняют следующим образом. В разряд базисных переводят ту свободную переменную, у которой больше абсолютное значение коэффициента. Затем в выше рассмотренном опорном плане проверяется, какая из базисных переменных при увеличении выбранной свободной переменной быстрее устремляется к нулю. Эту переменную переводят в разряд свободных.

Рассмотрим пример составления и решения линейной задачи симплекс-методом.

Пример 1. Пусть имеется следующая задача.

Цех выпускает валы и втулки. На производство 1 вала рабочий тратит 3 часа, а на производство 1 втулки - 2 часа. От реализации вала предприятие получает прибыль 800 руб., от реализации втулки - 600 руб. Цех должен выпустить не менее 100 валов и не менее 200 втулок. Сколько валов и втулок должен выпустить цех, чтобы получить наибольшую прибыль, если фонд рабочего времени составляет 900 человек - часов?

В качестве переменных (параметров) выбираем: - число валов, - число втулок. Затраты на выпуск 1 вала обозначим =3 час/вал, на выпуск 1 втулки - =2 час/втулка. Прибыль от реализации 1 вала =800 руб./вал, от реализации 1 втулки - =600 руб./втулка. Ресурсы рабочего времени =900 человек - часов. Условия по выпуску валов и втулок: , .

Таким образом, задача запишется в виде:

- множества параметров ;

- ограничения

- целевой функции .

Систему неравенств сведем к системе равенств:

где х₃ – недоиспользованный фонд рабочего времени,

х₄, х₅ – дополнительно выпущенные соответственно, валы и втулки.

Итак, для задачи, рассмотренной выше, запишем:

• целевую функцию (критерий эффективности)

;

• ограничения (область определения)

где - неиспользуемый ресурс времени, - дополнительно выпускаемые валы, - дополнительно выпускаемые втулки.

В рассматриваемом примере число неизвестных n=5, число уравнений m=3.

Решение: 1.Переменные х₄, х₅ принимаем за свободные. В качестве базовых переменных, выраженных через свободные, возьмем х₁, х₂, х₃. Составим опорный план:

Коэффициенты при х₄, х₅ отрицательные, следовательно, опорный план не оптимален. Переходим к построению нового опорного плана.

2. Из целевой функции видно, что в разряд базисных целесообразно перевести переменную х₄, а х₅ оставить свободной. Из числа базисных переменных в разряд свободных целесообразно перевести х₃. Тогда новый опорный план будет иметь вид:

Из целевой функции видно, что коэффициент при х₅ отрицательный, следовательно, план не оптимален. Переходим к составлению нового опорного плана.

3. Из разряда свободных переменных х₅ переводим в базисные, а из базисных переменных х₄ переводим в свободные. Составим опорный план вида:

Из целевой функции видно, что опорный план оптимальный. Следовательно, х₁=100, х₂=300, х₃=0, х₄=0, х₅=100 и в соответствии с поставленной задачей необходимо выпустить 100 шт. валов и 400 шт. втулок. При этом будут использованы все ресурсы, а прибыль составит 260 тысяч рублей.

Пример 2. Решим задачу ранее рассмотренного примера 3 (раскрой материала).

По условию задачи имеем:

- вектор переменных х=(х₁, х₂, х₃, х₄);

- ограничение:

3х₁+2х₂+х₃=800,

х₁+6х₂+9х₃+13х₄=400;

- целевую функцию

q(x)=12х₁+2х₂+4х₃.

Решение. Так как n=4, m=2, принимаем х₃=0, х₄=0.

Опорный план запишем в виде:

х₁=250+0,87х₃+1,62х₄ ,

х₂=25 - 1,64х₃ - 2,43х₄ ,

q(x)=3050+7,2х₃+14,6х₄ .

Решение найдено: число листов, раскроенных 1-м способом х₁=250 шт, вторым способом х₂=25 шт., третьим и четвёртым способом листы не раскраивались х₃=0, х₄=0.

При этом минимальные отходы q(х)=3050 м².