Верхняя и нижняя цены игры

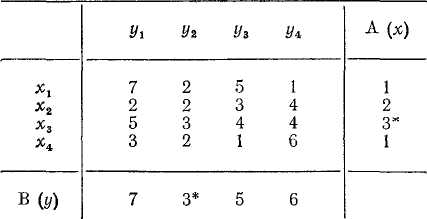
Для того чтобы понять принципы, которые лежат в основе выбора каждым игроком своей стратегии, рас­смотрим игру с матрицей, представленной табл. 8.

Таблица 8

Предположим, что первый игрок выбирает стратегию x_k. Если выигрыш L(x_k, у) будет зависеть от стратегии, которую выберет второй игрок. Например, при стратегии выигрыши первого игрока могут быть 7, 2, 5, 1. Может ли первый игрок рассчитывать на наибольший выигрыш, равный 7? Да, если он предположит, что второй игрок выбирает стратегию . Однако второй игрок может вы­брать любую другую стратегию, в том числе и . А тогда выигрыш первого игрока будет равен 1. Но уж меньше 1он быть не может ни при какой стратегии второго игро­ка. Поэтому 1, являющаяся наименьшим элементом мно­жества L(x₁, у) ={7, 2, 5, 1}, представляет собой гаран­тированный выигрыш первого игрока при стратегии . Обобщая приведенные рассуждения, видим, что если первый игрок применяет стратегию х_k, то он обеспечи­вает для себя гарантированный выигрыш А(х_k), равный наименьшему элементу множества L(x_k, у):

В теории игр предполагается, что игроки действуют достаточно осторожно, избегая необоснованного риска. В этом случае первый игрок должен выбирать такую стратегию , которая соответствует максимальному из чисел А(х). Обозначая гарантированный выигрыш первого игрока через  и называя его нижней чистой ценой игры, получаем:

Значения А(х), соответствующие игре с матрицей вида табл. 12, приведены в крайнем правом столбце. Значение  отмечено в этом столбце звездочкой.

Аналогичные рассуждения можно провести в отноше­нии второго игрока. Однако в матрице игры указаны его проигрыши, которые он стремится сделать минималь­ными. Рассмотрим стратегию у_k.. Эта стратегия может принести ему проигрыш, не больший чем

Для того чтобы обеспечить себе наименьшую величи­ну проигрыша, второй игрок должен применять такую стратегию , которая соответствует минимальному из чисел В (у). Обозначая величину проигрыша, которым может ограничиться второй игрок, через  и называя его верхней чистой ценой игры, получаем:

Значения В (у) для игры с матрицей вида табл. 12 приведены в нижней строке таблицы. Значение  отмече­но в этой строке звездочкой.

Нижняя цена игры, т. е. тот выигрыш, ко­торый может обеспечить себе первый игрок, не превы­шает верхней цены игры.

Цены и оптимальные стратегии игр

Простейшим частным случаем игры является случай, когда =. Обозначим эту величину через с. Именно к этому случаю относится игра с матрицей, заданной табл. 12, где ==3.

В данном случае никакой способ игры не может га­рантировать первому игроку выигрыш, больший, чем , так как именно величиной  второй игрок может ограни­чить свой проигрыш. С другой стороны, никакой способ игры не может гарантировать второму игроку проигрыш, меньший чем , так как первый игрок может гаранти­ровать себе выигрыш . Следовательно если  = =с, то никакая стратегия ни одного из игроков не может гаран­тировать ему лучшего результата, чем с. В то же время каждый игрок может гарантировать себе результат с. В этом случае с называется чистой ценой игры, а стратегии игроков, обеспечивающие результат с, на­зываются оптимальными стратегиями.

Клетка матрицы, определяющая величину с, назы­вается седловой точкой, так как значение с является максимумом столбца и минимумом строки, па пересече­нии которых стоит эта величина.