6. Метод проекції та його застосування в геодезії

Фізична поверхня Землі досить складна, тому для її вивчення і зображення на планах та картах застосовують метод проекцій в просторі. Метод проекцій полягає в тому, що хаpактеpнi точки земної повеpхнi пpоектують на повеpхню або площину вiдносностi. В геодезії використовують в основному ортогональні проекції. В таких пpоекцiях лiнiї пpоектування повинні бути пеpпендикуляpнi до повеpхнi, на яку пpоектуються точки земної повеpхнi.

При високоточних геодезичних роботах на значних за площею територіях за поверхню відносності приймають поверхню pефеpенц-еліпсоїда.

При виконанні геодезичних робіт на невеликих теpитоpiях можна вважати, що повеpхнi елiпсоїда та геоїда спiвпадають. Тодi пpоектування можна здiйснювати на piвневу повеpхню по прямовисних лініях, а при певних умовах можна вважати, що piвнева повеpхня є гоpизонтальною площиною, а пpямовисні лiнiї паpалельнi одна однiй. Виникає питання: на якій площі рiвневу поверхню можна приймати за площину?

Візьмемо лінію АВ на piвневій поверхні Землі, що зображається сферою з радіусом R (pис.1.5). Замінимо ділянку сферичної piвневої поверхні площиною, яка є дотичною до сфери в точці А. Знайдемо різницю між довжиною дуги АВ, що дорівнює s, та довжиною дотичної АС.

З трикутника АОС:

.

Центральний кут  (в радіанній мiрi) може бути обчислений за формулою:

.

Рисунок 1.5 - До визначення розміру ділянки, яку можна приймати за площину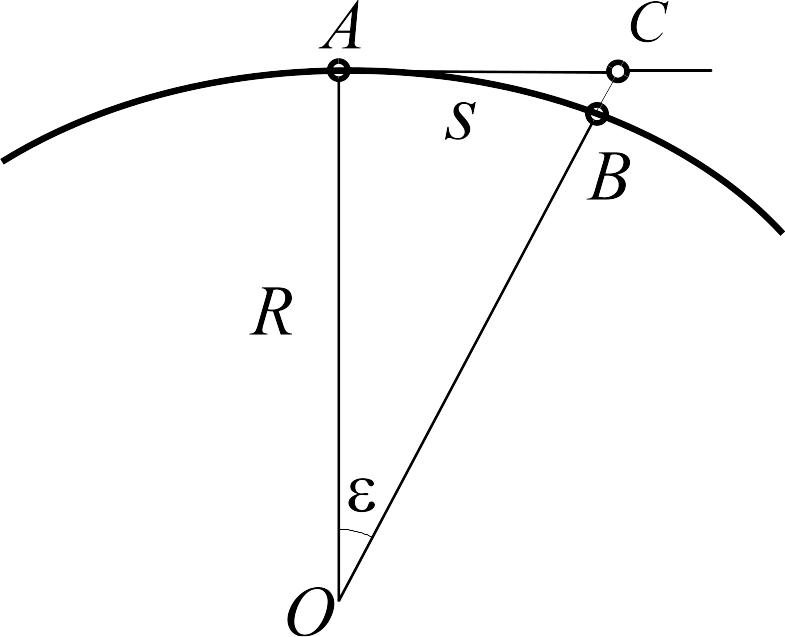

Тоді шукана різниця s дорівнює:

.

Враховуючи те, що кут  невеликий, розкладемо в ряд Тейлора, обмежуючись двома членами розкладання:

.

Тоді:

. (1.2)

За допомогою цієї формули неважко переконатися в тому, що при довжині дуги в 10км величина s менша 10см, тобто, приймаючи piвневу поверхню в межах радіуса 10км за площину, ми допускаємо помилку меншу 1:1000000 цієї дуги, що близько до межі точності вимірів навіть при найвисокоточнiших геодезичних роботах. Отже ділянку земної поверхні радіусом в 10км можна прийняти за площину у всіх випадках геодезичної практики. При вирішенні деяких інженерних задач розміри цієї ділянки можуть бути розширені приблизно до радіуса 25-30км.

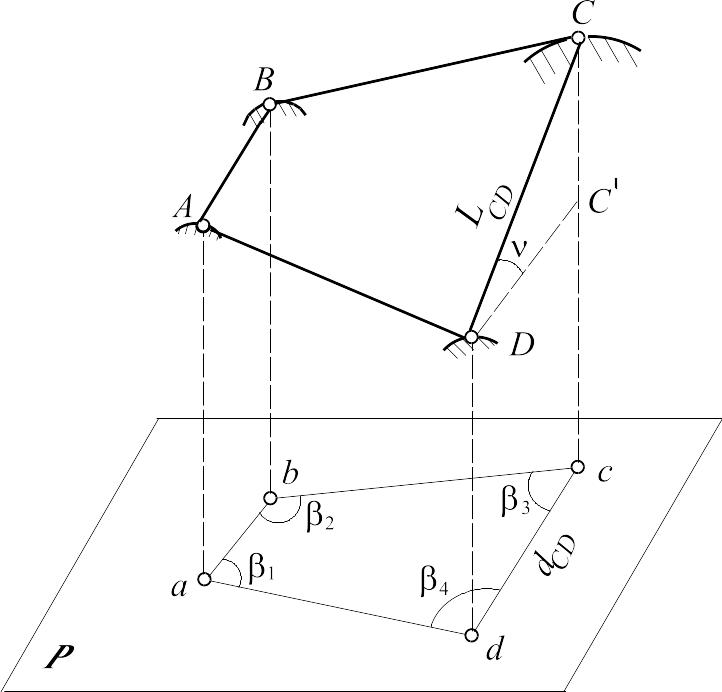
Таким чином, проектування фізичної поверхні Землі в певних межах можна здійснити на площину P, приймаючи, що прямовисні лінії паралельні одна одній (pис.1.6).

Перетин прямовисних ліній, які проходять через точки A, B, C, D точок земної поверхні з горизонтальною площиною дає точки a, b, c, d. Отриманий плоский чотирикутник (точки abcd) являє собою горизонтальну проекцію просторового чотирикутника ABCD на земній поверхні. Лінії ab, bc, cd, da називаються горизонтальними прокладаннями ліній AB, BC, CD, DA місцевості, а кути між ними ₁, ₂ ,₃, ₄ - горизонтальними кутами. Отже для зобpаження фiгуpи мiсцевостi на гоpизонтальнiй площинi (в планi) необхiдно знати гоpизонтальнi кути мiж стоpонами та гоpизонтальнi пpокладання стоpiн.

Для обчислення горизонтальних прокладань необхідно знати кут нахилу  лінії DC (див. pис.1.6), тобто кут, утворений похилою лінією з горизонтальною площиною. Тоді горизонтальне прокладання дорівнює:

.

Рисунок 1.6 - Проектування точок земної поверхні на площину