Международный университет природы, общества и человека

«Дубна»

Кафедра распределенных информационно-вычеслительных систем

Курсовая работа

по программированию на языках высокого уровня

на тему:

«Калькулятор матриц»

Выполнила: студентка группы 1013

Решетников С.А.

Руководители: ст. преп. Андреев В.А.,

ст. преп. Мурадян А.В.

Дубна, 2010

Оглавление

Введение 3

Постановка задачи 4

Теоретическая часть 5

Описание программы 8

Листинг программы 11

Список литературы 14

Введение

Передо мной была поставлена задача разработать программу для работы с матрицами, выполняющая основные математические операции: сложение, вычитание, умножение, транспонирование, определитель, поиск обратной матрицы.

В пункте «Постановка задачи» ставится цель разработать программу для осуществления арифметических операций над матрицами. Далее идет пункт «Теоретическая часть», затем пункт «Описание программы», блок-схема данной программы, пример наиболее интересного алгоритма программы и заключение, перечисляющее основные результаты курсовой работы.

Постановка задачи

Цель работы: разработать программу для работы с матрицами на языке C# .

Исходные данные: для работы с программой используются тестовые данные в виде матриц.

Представления о модели: при работе с этой программой пользователь должен иметь возможность:

1. вводить данные с помощью клавиатуры;

2. изменять ранее введенные данные;

3. наглядно видеть результаты работы с программой в виде матриц;

4. обращаться за помощью в меню «помощь»;

Результат: программа, позволяющая осуществлять основные арифметические операции над матрицами, написанная на языке C#.

Критерий результата: программа должна отвечать следующим требованиям:

1. иметь удобный и понятный интерфейс, во многом упрощающий работу пользователя;

2. иметь защиту от некорректно введенных данных;

Теоретическая часть

Матрица — математический объект, записываемый в виде прямоугольной таблицы чисел и допускающий алгебраические операции (сложение, вычитание, умножение и др.) между ним и другими подобными объектами.

Правила выполнения операций над матрицами сделаны такими, чтобы было удобно записывать системы линейных уравнений.

Обычно матрицу обозначают заглавной буквой латинского алфавита и выделяют круглыми скобками «(…)» (встречается также выделение квадратными скобками «[…]», двойными прямыми линиями "||…||").

Числа, составляющие матрицу (элементы матрицы), часто обозначают той же буквой, что и саму матрицу, но строчной.

У каждого элемента матрицы есть 2 нижних индекса (a_ij) — первый «i» обозначает номер строки, в которой находится элемент, а второй «j» — номер столбца. Говорят «матрица размерности », подразумевая, что в матрице m строк и n столбцов

История.

Понятие матрицы впервые появилось в середине XIX века в работах Уильяма Гамильтона и Артура Кэли. Фундаментальные результаты в теории матриц принадлежат Вейерштрассу, Жордану, Фробениусу.

Операции над матрицами.

Пусть a_ij — элементы матрицы A, а b_ij — элементы матрицы B.

Линейные операции.

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен

b_ij = λa_ij.

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен

c_ij = a_ij + b_ij.

Вычитание матриц A − B определяется аналогично сложению, это операция нахождения матрицы C, элементы которой

c_ij = a_ij− b_ij.

Сложение и вычитание допускается только для матриц одинакового размера.

Существует нулевая матрица Θ такая, что её прибавление к другой матрице A не изменяет A, то есть

A + Θ = A.

Все элементы нулевой матрицы равны нулю.

Нелинейные операции.

Умножение матриц (обозначение: AB, реже со знаком умножения ) — есть операция вычисления матрицы C, элементы которой равны сумме произведений элементов в соответствующей строке первого множителя и столбце второго.

.

В первом множителе должно быть столько же столбцов, сколько строк во втором. Если матрица A имеет размерность , B — , то размерность их произведения AB = C есть . Умножение матриц не коммутативно.

Умножение матриц ассоциативно. Возводить в степень можно только квадратные матрицы.

Транспонирование матрицы (обозначение: A^T) — операция, при которой матрица отражается относительно главной диагонали, то есть

.

Если A — матрица размера , то A^T — матрица размера .

Обратная матрица — такая матрица A^-1, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

AA ^{− 1} = A ^{− 1}A = E.

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и сингулярных матриц обратных матриц не существует. Однако, возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Теорема . Для того, чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Матрица, обратная матрице А, обозначается через А ^{- 1} , так что В = А ^{- 1} . Обратная матрица вычисляется по формуле

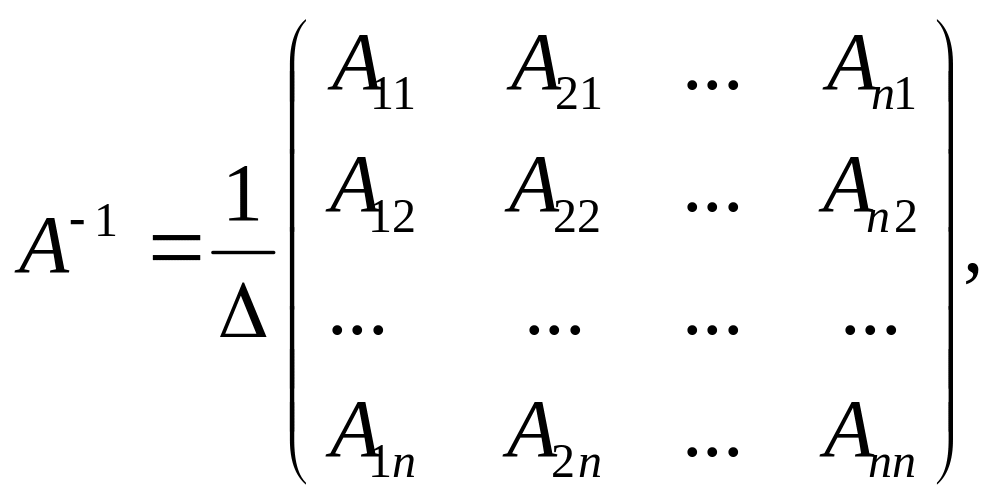
где А _{i j} — алгебраические дополнения элементов a _{i j}.