1.7. Полиномальная регрессия для табличных данных
В MATLAB 6 и выше имеется возможность ускорить процесс аппроксимации. Для этого в пункте Tools графического окна имеются две команды:
- Basic Fiting – основные виды аппроксимации (регрессии),
- Data Statistics – статистические параметры данных.
Команда Basic Fiting открывает окно, дающее доступ к ряду видов аппроксимации и регрессии: сплайновой, эрмитовой и полиномальной со степенями от 1 (линейная аппроксимация) до 10, в том числе со степенью 2 (квадратичная аппроксимация) и 3 (кубическая аппроксимация). Команда Data Statistics открывает окно с результатами простейшей статистической обработки данных.
Открыв окно Basic Fiting, можно задать в основном окне MATLAB некоторую зависимость векторами координат ее точек:
>> X=[2,4,6,8,10,12,14];
>> Y=[ 3,7.6,4.4,5.1,5,5.6,6.6];
>> plot (X,Y);
После выполнения последней команды появляется окно результатов аппроксимации. При проведении полиномальной аппроксимации надо помнить, что максимальная степень полинома на 1 меньше числа точек, т.е. числа элементов в векторах X и Y.
В окне сессии MATLAB (видим вверху, слева), выполнив команду Tools – Basic Fitting, можно получить окно регрессии (окно Basic Fitting). В этом окне флажками можно отметить устанавливаемый порядок полиномальной регрессии. Установка флажка Show equations выводит в графическом окне запись выбранных уравнений регрессии.
По команде Tools – Data Statistics выводится окно Data Statistics с рядом статистических параметров. Средства обработки данных графического окна позволяют строить столбчатый или линенйчатый графики погрешностей в узловых точках и наносить на эти графики норму погрешности. Норма дает статистическую оценку среднеквадратичной погрешности. Для вывода графика погрешности надо установить флажок Plot residuals и в меню под этим флажком выбрать тип графика.
На рисунке ниже приведено окно для аппроксимации приведенной выше последовательности данных полиномом 3-й и 5-й степени.
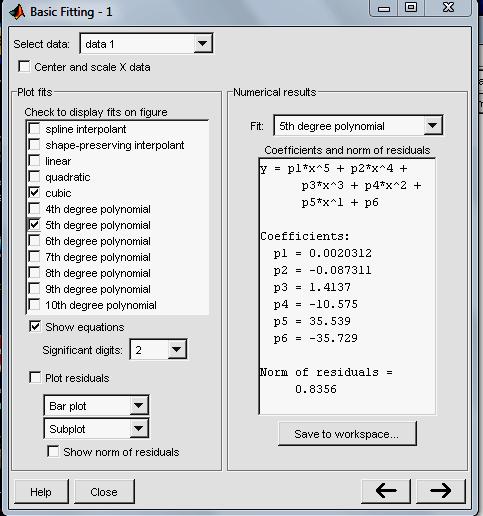
На нижнем рисунке показаны исходный график (ломанная линия) и аппроксимирующие кривые, а также формулы для полученных кривых.
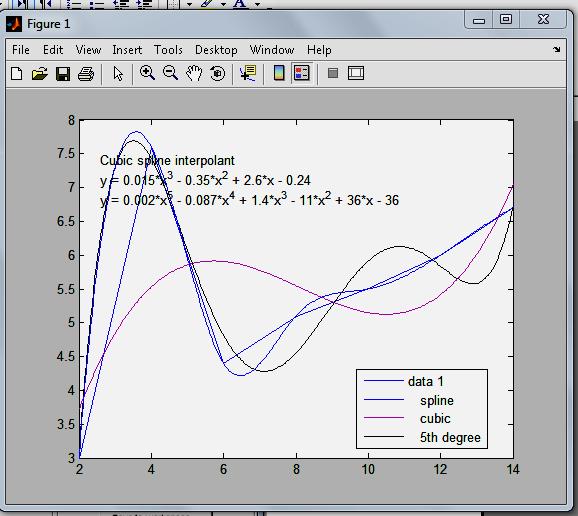
2. Характеристики средств измерения
Класс точности — основная метрологическая характеристика прибора, определяющая допустимые значения основных и дополнительных погрешностей, влияющих на точность измерения.
Погрешность может нормироваться, в частности, по отношению к:
- результату измерения (по относительной погрешности), в этом случае, по ГОСТ 8.401-80 цифровое обозначение класса точности (в процентах) заключается в кружок.
- длине (верхнему пределу) шкалы прибора (по приведенной погрешности)
Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0 — 30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.
Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.
Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.
Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.
Стрелочные электроизмерительные приборы по допустимым значениям погрешностям делятся на классы точности, которые обозначены на шкалах приборов числами 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0. Класс точности пр прибора показывает, сколько процентов составляет абсолютная погрешность от всей шкалы прибора.
пр = (иА/Амакс)*100% .
Например абсолютная инструментальная погрешность прибора класса 2,5 составляет 2,5% от его шкалы.
Если известен класс точности прибора и его шкала, то можно определить абсолютную инструментальную погрешность измерения
иА=(пр * Амакс)/100.
Для повышения точности измерения стрелочным электроизмерительным прибором надо выбирать прибор с такой шкалой, чтобы в процессе измерения располагались во второй половине шкалы прибора.