1.6. Сплайновая и эрмитова интерполяция.
Сплайновая интерполяция выполняется по трем ближайшим точкам, причем эти тройки точек постепенно перемещаются от начала к концу массива точек, каждый раз сдвигаясь на одну точку. Кроме того непрерывность первой и второй производных при сплайновой интерполяции делает кривую очень плавной. Сплайновая интерполяция выполняется аналогично построению кривой при черчении по лекалу.
Методы аппроксимации функций с помощью сплайнов, предложенные впервые в 40-х годах, получили широкое распространение только в последнее время.
Основной недостаток интерполяционных многочленов как аппарата приближения функций, применяемого для восстановления дискретизированных сигналов, состоит в том, что поведение этих многочленов в окрестности какой-либо точки определяет их поведение в целом. Если исследуемый сигнал на разных участках ведет себя по-разному, например на одном участке постоянен, а затем круто убывает или возрастает и т.д., использование интерполяционных многочленов хороших результатов не дает. В таких случаях лучше пользоваться сплайнами.
Английское слово spline означает «упругая рейка». Такую рейку используют в качестве гибкого лекала при вычерчивании плоских кривых по опорным точкам.
Основная идея применения сплайнов состоит в следующем. Интервал, на котором восстанавливают функцию, разбивают на подинтервалы, на каждом из которых функцию задают полиномом достаточно низкой степени и обеспечивают непрерывность кривой в точках “склейки” путем приравнивания значений полиномов на границах подинтервалов. На рисунке выше приведен пример сплайновой интерполяции приведенных данных, она ближе всего отображает график исходной зависимости, но не имеет аналитического выражения.
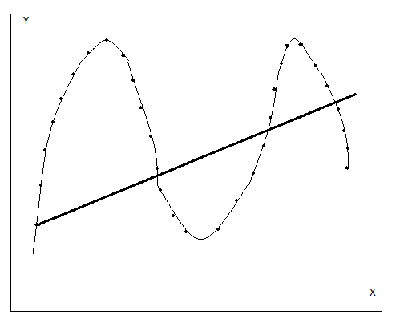
На рисунке приведен пример особенности сплайновой интерполяции. Если задано n точек, то при полиномальной аппроксимации получим, даже при высоком порядке полинома, некоторую кривую, которая прорезает заданный массив точек (толстая линия на графике). Если применить сплайновую аппроксимацию, то получаем кривую отображающую характер расположения точек на плоскости. Причина разницы кроется в особенности сплайновой интерполяции – она выполняется по трем ближайшим точками и эти тройки точек постепенно перемещаются.
MATLAB дает возможность в графическом окне использовать еще один вид интерполяции на основе полиномов третей степени Эрмита. Сплайн Эрмита — сплайн, построенный из многочленов в форме Эрмита. Наиболее распространён кубический сплайн Эрмита. Принцип интерполяции тот же, что и при сплайновой интерполяции. Полиномы Эрмита имеют более гибкие линии, чем сплайны. Они точнее следуют за отдельными изгибами исходной зависимости.
Шарль Эрми́т (фр. Charles Hermite; 24 декабря 1822, Дьёзе, Лотарингия, Франция — 14 января 1901, Париж, Франция) — французский математик.
Основные работы в теории чисел, теории квадратичных форм, теории нвариантов, ортогональных нвариантов, ортогональных многочленов, эллиптических функций и в алгебре.
Наиболее известным его учеником был Анри Пуанкаре.
Эрмит показал, что число e (основание натурального логарифма) является трансцендентным.
Эти два подхода нельзя называть полноценной интерполяцией, поскольку в данном случае нет единого выражения для всей совокупности аппроксимирующих точек. На каждом отрезке используется кубический полином с новыми коэффициентами. Поэтому и вывода аппроксимирующей функции в поле графика (в MATLABе) не предусмотрено.
Эрмитова интерполяция лучше отслеживает быстрые изменения исходных данных, но имеет худшие сглаживающие свойства.
Можно сформулировать следующую практическую рекомендацию. Если у вас имеется достаточно большой массив экспериментальных точек на плоскости, то для выбора аппроксимирующей зависимости целесообразно предварительно провести сплайновую или эрмитову интерполяцию для общей оценки экспериментальной зависимости для последующей аналитической интерполяции.