- •В.А.Чащин технология испытаний механизмов приводов
- •Технология испытаний механизмов приводов
- •1. Испытания приводов
- •1.1. Общие положения
- •1.2. Некоторые понятия математической статистики
- •1.3. Определение параметров функций по экспериментальным данным
- •1.4. Метод наименьших квадратов
- •1.5. Применение метода наименьших квадратов при аппроксимации апериодических зависимостей.
- •1.6. Сплайновая и эрмитова интерполяция.
- •1.7. Полиномальная регрессия для табличных данных
- •2. Характеристики средств измерения
- •Погрешность отсчета
- •3.1. Полная абсолютная погрешность прямых измерений
- •Запись окончательного результата прямого измерения
- •3.3. Погрешности косвенных измерений
- •Обработка результатов прямого измерения
- •4. Технические паспорта изделий
- •4.1. Технический паспорт газового привода.
- •4.2. Технический паспорт гидропривода.
- •5. Типовые схемы испытаний
- •5.1. Статические характеристики
- •5.2. Скоростная характеристика.
- •5.3. Потенциометры
- •5.4. Приборы для измерения скорости. Тахогенератор.
- •Тахогенераторы постоянного тока.
- •Синхронные тахогенераторы.
- •Асинхронные тахогенераторы.
- •5.5. Измерение линейных перемещений
- •5.5. Силовая характеристики.
- •5.6. Манометры
- •Разновидности манометров:
- •5.7. Механическая характеристика.
- •5.8. Определение расхода
- •5.9. Ротаметры Ротаметр — прибор для определения объёмного расхода газа или жидкости в единицу времени.
- •Достоинства ротаметров:
- •Недостатки
- •Автоматизированные ротаметры.
- •Датчик массового расхода воздуха Устройство
- •Применение
- •6.1. Динамические характеристики
- •6.2. Расшифровка результатов испытаний
- •6.3. Стенд
1.4. Метод наименьших квадратов
Если некоторая физическая величина зависит от другой величины, то эту зависимость можно исследовать, измеряя y при различных значениях x . В результате измерений получается ряд значений:
x1, x2, ..., xi, , ... , xn;
y1, y2, ..., yi, , ... , yn.
По данным такого эксперимента можно построить график зависимости y = ƒ(x). Полученная кривая дает возможность судить о виде функции ƒ(x). Однако постоянные коэффициенты, которые входят в эту функцию, остаются неизвестными. Определить их позволяет, как говорилось выше, метод наименьших квадратов. Экспериментальные точки, как правило, не ложатся точно на кривую. Метод наименьших квадратов требует, чтобы сумма квадратов отклонений экспериментальных точек от кривой, т.е. [yi – ƒ(xi)]2 была наименьшей.
На практике этот метод наиболее часто (и наиболее просто) используется в случае линейной зависимости, т.е. когда
y = kx или y = a + bx.
Линейная зависимость очень широко распространена в практике испытаний. И даже когда зависимость нелинейная, обычно стараются строить график так, чтобы получить прямую линию.
Рассмотрим зависимость y = kx (прямая, проходящая через начало координат). Составим величину φ – сумму квадратов отклонений наших точек от прямой
![]() .
.
Величина φ всегда положительна (т.к квадрат) и оказывается тем меньше, чем ближе к прямой лежат наши точки. Метод наименьших квадратов утверждает, что для k следует выбирать такое значение, при котором φ имеет минимум, т.е.
![]()
откуда
![]()
Рассмотрим теперь несколько более трудный случай, когда точки должны удовлетворить формуле y = a + bx (прямая, не проходящая через начало координат).
Задача состоит в том, чтобы по имеющемуся набору значений xi, yi найти наилучшие значения a и b.
Снова составим квадратичную форму φ, равную сумме квадратов отклонений точек xi, yi от прямой
![]()
и найдем значения a и b , при которых φ имеет минимум
![]() ;
;
![]() .
.
.
Совместное решение этих уравнений дает
![]()
![]() .
.
1.5. Применение метода наименьших квадратов при аппроксимации апериодических зависимостей.
Часто экспериментальные зависимости заведомо описываются дифференциальными уравнениями первого порядка (например, нарастание тока в обмотках управления, нарастание давления в полостях силового цилиндра), решением которых являются экспоненты. По результатам экспериментальных измерений желательно определить параметры экспоненты. Для получения исходных данных необходимо провести эксперимент – подать на вход элемента скачек сигнала и записать реакцию на выходе.
Для упрощения расчетов желательно нормировать полученные экспериментальные данные: совместить начало процесса с началом координат, установившееся значение выходной величины принять равной 1. В этом случае мы будем искать аппроксимирующую зависимость в виде
G = 1 – e-kx ,
или
G = 1 – e-(x/T) ,
здесь G- реакция системы, х- входной сигнал системы, k = 1/T.
Как и ранее составим величину φ – сумму квадратов отклонений экспериментальных точек от экспоненты
φ = ∑(yi -1 + e-kxi )2 .
Как и ранее для k следует выбирать такое значение, при котором φ имеет минимум, т.е.
dφ/dk = -2 ∑(yi -1 + e-kxi )kxi = 0,
т.к. 2 ≠ 0, kxi ≠ 0, то (???e-kxi ≠ 0 ???),
то yi -1 + e-kxi = 0,
откуда
e-kxi = 1 - yi .
Если в последнем уравнении взять натуральный логарифм от левой и правой частей, то получим
- kxi = ln(1 – yi),
и далее
k = - (ln(1- yi))/xi.
Если есть предположение, что рассматриваемый процесс может быть удобно описан экспонентой то по полученной формуле нужно определить 3 – 4 значения коэффициента k, затем определить среднее значение k. Предварительно нужно пронормировать экспериментальные данные как указывалось выше.
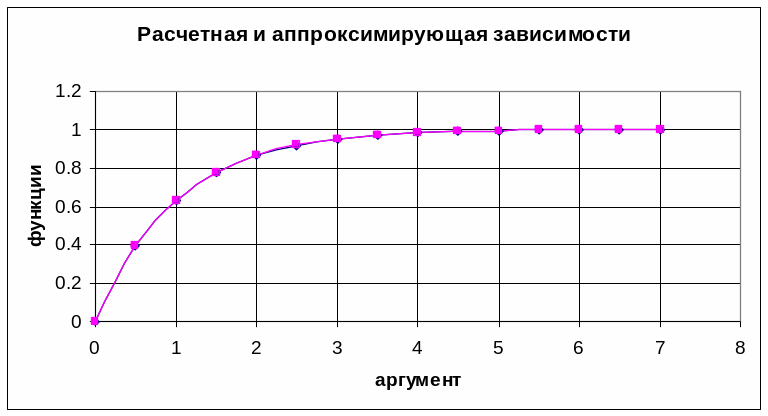
Примеры: Рассмотрим определение показателя для функции y = 1-e-x
В первом столбце таблицы приведены значения аргумента х, во втором столбце приведены рассчитанные значения функции у. Выберем на расчетном графике три точки:
1) хi = 0,5 yi = 0,39
k = - (ln(1- yi))/xi = - (ln(1- 0,39))/0,5 = - (ln0,61)/0,5 = - 2,303*log(0,61)/0,5= 0,99. (Примечание: log(0,61) – число отрицательное)
2) хi = 1 yi = 0,63
k = - (ln(1- yi))/xi = -(ln(1- 0,63))/1 = - (ln0,37)/1 = 2,303*log(0,37)/1 = 0,99.
3) хi = 6 yi = 0,998
k =- (ln(1- yi))/xi = (ln(1- 0,998))/6 = = - 2,303(log (-0,002))/6= 1,04.
Примечание: число – 2,303 – модуль перехода от натуральных логарифмов к десятичным.
Определяем среднее значение k.
k = (0,99 + 0,99 + 1,04)/3 = 1,006.
С полученным показателем степени строится график по данным третьего столбца. В пределах точности построения оба графика совпали.
|
k = 1 |
k = 1.006 |
0 |
0 |
0 |
0.5 |
0.393469 |
0.395286 |
1 |
0.632121 |
0.634321 |
1.5 |
0.77687 |
0.778869 |
2 |
0.864665 |
0.866279 |
2.5 |
0.917915 |
0.919137 |
3 |
0.950213 |
0.951101 |
3.5 |
0.969803 |
0.97043 |
4 |
0.981684 |
0.982119 |
4.5 |
0.988891 |
0.989187 |
5 |
0.993262 |
0.993461 |
5.5 |
0.995913 |
0.996046 |
6 |
0.997521 |
0.997609 |
6.5 |
0.998497 |
0.998554 |
7 |
0.999088 |
0.999126 |
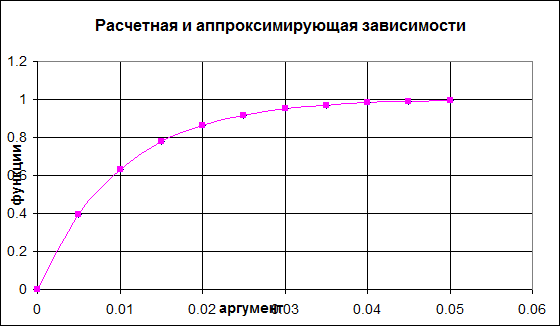
Пример 2: Рассмотрим определение показателя для функции
y = 1-e-0.01x . В первом столбце таблицы приведены значения аргумента х, во втором столбце приведены рассчитанные значения функции у. Выберем на расчетном графике три точки:
|
k=100 |
K=100,1 |
0 |
0 |
0 |
0.005 |
0.393469 |
0.393773 |
0.01 |
0.632121 |
0.632488 |
0.015 |
0.77687 |
0.777204 |
0.02 |
0.864665 |
0.864935 |
0.025 |
0.917915 |
0.91812 |
0.03 |
0.950213 |
0.950362 |
0.035 |
0.969803 |
0.969908 |
0.04 |
0.981684 |
0.981757 |
0.045 |
0.988891 |
0.988941 |
0.05 |
0.993262 |
0.993296 |
1) хi = 0,005 yi = 0,4
k = - (ln(1- yi))/xi = -(ln(1- 0,4))/0,005 = - 2,303(lg 0,6)/0,005= 102,3.
2) хi = 0,015 yi = 0,777
k = - (ln(1- yi))/xi = -(ln(1- 0,777))/0,015 = - 2,303(lg 0,222)/0,015 = 100,1.
3) хi = 0,025 yi = 0,918
- (ln(1- yi))/xi = (ln(1- 0,918))/0,025 = = - 2,303(lg(0,082))/0,025= 100,1.
Определяем среднее значение k.
k = (102, 3 + 100,1 + 100,1)/3 = 100,8.
С полученным показателем степени строится график по данным третьего столбца. В пределах точности построения опять оба графика совпали.