Розрахунок значень сезонної компоненти в адитивній моделі

Показник	Рік	Номер кварталу
		І	ІІ	ІІІ	ІV
	2010	-	-	554,38	422,75
	2011	-979,75	-160,13	869,38	526,00
	2012	-1151,00	-21,88	752,88	522,13
	2013	-1181,88	-	-	-
Разом за і-й квартал (за всі роки)		-3312,625	-182	2176,625	1470,875
Середня оцінка сезонної компоненти для і-го кварталу, Ś(i)		-1104,208333	-91	725,5416667	490,2916667
Скоригована сезонна компонента, S(i)		-1109,36	-96,16	720,39	485,14

Для даної моделі:- 1104,21+ -91 + 725,54 + 490,29 = 20,625.

Знайдемо коефіцієнт коригування: k=20,625:4=5,16.

Розрахуємо скориговані значення сезонної компоненти як різницю між її середньою оцінкою і коефіцієнтом коригування k :

S_i = Ś_i – k, i = 1,2,3,4 (1.1)

У моделях з сезонною компонентою припускається, що сезонні впливи за період взаємопогашуються. Для адитивної моделі це означає, що сума значень сезонної компоненти для цих кварталів повинна дорівнювати нулю. Перевіримо цю умову: -1109,36 - 96,16 + 720,39 + 485,14 = 0. Отже, одержані такі значення сезонної компоненти:

1 квартал S₁ = -1109,36;

2 квартал S₂ = - 96,16;

3 квартал S₃ = 720,39;

4 квартал S₄ = 485,14.

3. Елімінуємо вплив сезонної компоненти. Для цього віднімемо її значення від кожного рівня початкового часового ряду. Одержимо величини T+S=Y-S (гр. 5 табл.1.6). Ці значення розраховуються за кожний момент часу і містять тільки тенденцію і випадкову компоненту.

Таблиця 1.6

Розрахунок вирівняних значень (t) і похибок (е) в адитивній моделі

Рік	Квартал	Yt	S(i)	T+E=Y-S	t	T	Yprog=T+S	Відносна похибка
2010	1	4 737	-1109,36	5 846	1	5894,600	4785,240	0,010
	2	5 597	-96,16	5693,16	2	6066,200	5970,040	0,067
	3	6 567	720,39	5846,61	3	6237,800	6958,190	0,060
	4	6 699	485,14	6213,86	4	6409,400	6894,540	0,029
2011	1	5 638	-1109,36	6747,36	5	6581,000	5471,640	0,030
	2	6 805	-96,16	6901,16	6	6752,600	6656,440	0,022
	3	8 091	720,39	7370,61	7	6924,200	7644,590	0,055
	4	7 954	485,14	7468,86	8	7095,800	7580,940	0,047
2012	1	6 435	-1109,36	7544,36	9	7267,400	6158,040	0,043
	2	7 659	-96,16	7755,16	10	7439,000	7342,840	0,041
	3	8 501	720,39	7780,61	11	7610,600	8330,990	0,020
	4	8 303	485,14	7 818	12	7782,200	8267,340	0,004
2013	1	6 624	-1109,36	7733,36	13	7953,800	6844,440	0,033
	2	7 732	-96,16	7828,16	14	8125,400	8029,240	0,038
	3	8 628	720,39	7907,61	15	8297,000	9017,390	0,045
	4		485,14		16	8468,600	8953,740
2014	1		-1109,36		17	8640,200	7530,840
	2		-96,16		18	8811,800	8715,640
	3		720,39		19	8983,400	9703,790
	4		485,14		20	9155,000	9640,140

4. Знайдемо компоненту Т даної моделі. Для цього проведемо аналітичне вирівнювання ряду (T+Е) за допомогою лінійного тренду.

Результати вимірювання такі: Т=5723 + 171,6*t, R²=0,871. Підставляючи в це рівняння t=1,2,…,20, знайдемо рівні Т для кожного моменту часу (гр. 7 табл. 1.6.

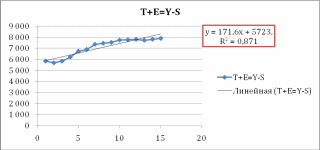
Рис. 1.5. Аналітичне вирівнювання тренду

5. Знайдемо значення рівнів ряду, одержані за адитивною моделлю.

Для цього додамо до рівнів Т значення сезонної компоненти для відповідних кварталів.

6. Розрахуємо абсолютні похибки Е=Y-(T+S).

Чисельні значення відносних похибок наведені в гр. 9 табл. 1.6.

Також обраховуємо середнє значення відносної похибки. Її значення становить 3,6%.

Висновок: Отже, побудована нами адитивна модель пояснює 96,4 % загальної варіації рівнів часового ряду розміру ВВП на душу населення України за останні 15 кварталів.

Необхідно дослідити залежність між обсягами активів та фінансовим результатом I групи банків (європейських), які діють на території України.

Дані показники відображено на графіку:

Рис. 9 Динаміка залежності обсягу активів та фінансового результату європейських банків

Дну модель найкраще описує поліноміальна функція 6 порядку, таким чином одержано R² = 0.90.

За допомогою пакету "Аналіз даних" одержано наступні результати:

Коефіцієнт детермінації R² = 0.90, це означає, що на 90% зміна фінансового результату пояснюється зміною величини активів, і лише 10% припадає на інші факторні ознаки, не враховані в даному дослідженні, тобто модель є якісною. Оскільки статистичне значення критерію Фішера F_cmam =0,04 < F_Kp (0,05;1,6) = 5,987, то модель визнається неадекватною, тобто неякісною.

Необхідно дослідити залежність між обсягами активів та фінансовим результатом I групи банків (російських), які діють на території України.

Рис. 10 Динаміка залежності обсягу активів та фінансового результату російських банків

Дну модель найкраще описує поліноміальна функція 6 порядку, таким чином одержано R² = 0.75.

За допомогою пакету "Аналіз даних" одержано наступні результати:

Коефіцієнт детермінації R² = 0.75, це означає, що на 75% зміна фінансового результату пояснюється зміною величини активів, і лише 25% припадає на інші факторні ознаки, не враховані в даному дослідженні, тобто модель є якісною.

Оскільки статистичне значення критерію Фішера F_cmam =0,03 < F_Kp (0,05;1,6) = 5,987, то модель визнається неадекватною, тобто неякісною.

Необхідно дослідити залежність між обсягами активів та фінансовим результатом I групи банків (українських), які діють на території України.

Отже, в роботі проаналізовано залежність між обсягами активів та фінансовим результатом українських банків, які входять до I групи за класифікацією НБУ.

Період	Українські банки (I групи)
	активи	ФР
2006	84 001 548	963 919
2007	148 232 847	1 614 976
2008	230 300 448	2 364 132
2009	269 884 683	-4 734 106
2010	312 984 266	-2 600 469
2011	389 341 217	-3 659 613
2012	468 929 415	1 963 495
2013	522 560 744	3 518 239

Дані показники відображено на графіку:

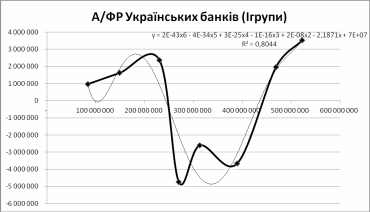
Рис. 11 Динаміка залежності обсягу активів та фінансового результату українських банків

Дну модель найкраще описує поліноміальна функція 6 порядку, таким чином одержано R² = 0.80.

За допомогою пакету "Аналіз даних" одержано наступні результати:

Дисперсионный анализ
	df		SS		MS		F		Значимость F
Регрессия	1,00		486385560140,77		486385560140,77		0,04		0,84
Остаток	6,00		67399770091758,50		11233295015293,10
Итого	7,00		67886155651899,30

	Коэффициенты	Стандартная ошибка	t-статистика	P-Значение	Нижние 95%	Верхние 95%
Y-пересечение	-597350,8749	2792545,704	-0,213909077	0,837701951	-7430464,039	6235762,289
Переменная X 1	0,001734943	0,008337743	0,208083074	0,842047643	-0,018666778	0,022136665

Коефіцієнт детермінації R² = 0.80, це означає, що на 80% зміна фінансового результату пояснюється зміною величини активів, і лише 20% припадає на інші факторні ознаки, не враховані в даному дослідженні, тобто модель є якісною. Однак не варто ідеалізувати значимість даного коефіцієнта, адже існує безліч прикладів неправильно специфікованих моделей з високим коефіцієнтом детермінації. Тому коефіцієнт детермінації розглядаємо як один з декількох показників, які треба проаналізувати, щоб уточнити побудовану модель.

Варто перевірити дану модель за критерієм Стьюдента:

Так, у роботі обчислено t-статистики для критерію Стьюдента оцінки статистичної значимості параметрів моделі. З таблиць критичних точок розподілу Стьюдента для а = 0,05 і ступенів вільності 6, враховуючи двосторонню критичну область критерію, знаходимо t_двкр (0,05; 6) = 2,447. Оскільки t_стат> t_двкр, то параметр статистично значимий. А це означає, що обсяг активів є значимою в даній моделі і її вплив на фінансовий результат є суттєвим. Інтервали довіри для відповідних параметрів моделі задають межі, в яких з ймовірністю 0,95 коливатимуться значення відповідних параметрів. Так, даний параметр, накривається інтервалом /с/Д =(-0,0187; 0,0221) з ймовірністю 0,95.

Також варто перевірити якість моделі за критерієм Фішера, для цього за таблицями критичних точок розподілу Фішера знаходимо критичну точку F_Kp(a;m,n-m-1), де т - кількість незалежних змінних моделі, п - обсяг вибірки. Оскільки статистичне значення критерію Фішера F_cmam =0,04 < F_Kp (0,05;1,6) = 5,987, то модель визнається неадекватною, тобто неякісною.

Отже, побудовано модель залежності фінансового результат банку від обсягу активів банку. В моделі високий коефіцієнт детермінації, висока t-статистики, але F-критерій є незначимим. Все це дає підстави вважати побудовану модель з однієї сторони якісною, а з іншої - залишає нам ще варіанти для покращення моделі.