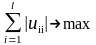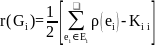Лекция 7 Итерационные алгоритмы разрезания графа на куски

Суть итерационных алгоритмов разрезания графов заключается в выборе первого случайного разрезания с дальнейшими перестановками вершин с одного куска в другой с целью минимизации числа соединительных ребер.

Вспомним, что матрица смежности для графа G(X,E), имеющего n вершин – это матрица R=||r_ij||_n*n, элементы которой соответствуют числу ребер, соединяющих вершину x_i с вершиной x_j.

Т.к. матрица смежности полностью описывает граф, то разрезание графа G на l кусков G₁, G₂, … , G_l эквивалентно разбиению матрицы смежности R графа G на l клеток (подматриц).

Клетки по главной диагонали задают подграфы G_i^’, включающиеся в куски G_i, а остальные клетки определяют наличие ребер между кусками.

За критерий оптимальности можно брать минимум числа ребер между кусками (см. формулу(3.2) лекции 3)

(7.1)

,

либо максимум числа ребер внутри кусков

	(7.2)
или G → max	(7.3)

(Согласно материалу лекции 3 множество U_ij определяет подмножество ребер U_ij ≤ U, попадающих в разрез между кусками G_i и G_j графа G, а множество U_ii определяет подмножество ребер, т.е. кол-во связей внутри куска G_i),

Разрезание графа будем сводить на каждом шаге к разрезанию графа на два куска. Число вершин первого куска равно числу вершин выделяемого куска, а число вершин второго куска – числу всех оставшихся вершин графа.

Таким образом, в первом куске пусть будет множество Е_i вершин, а во втором Е_i = Е \ Е_i.

Тогда множество ребер разобьем на три класса:

1) внутренние ребра, лежащие в куске; G_i;

2) внешние ребра, лежащие в куске G_i;

3) соединяющие ребра между кусками G_i и G_i.

Число внутренних ребер куска G_i равно

(7.4)

Где (e_i) - сумма локальных степеней вершин куска G_i, K_ii - число соединительных ребер кусков G_i и G_i

Число внешних ребер, которые являются внутренними для куска G_i равно

(7.5)

Для каждой вершины ek введем число связности вершины (разность кол-ва внешних и внутренних связей k-го элемента)

k=

rk(Gi)- rk(Gi), если ekEi rk(Gi)- rk(Gi), если ekEi

(7.6) (7.7)

Где:

• r_k(G_i) - число ребер, соединяющих вершину e_k с вершинами куска G_i (k-й элемент, i-й кусок);

• r_k(G_i) - число ребер, соединяющих вершину e_k с вершинами куска G_i.

Обозначим:

• _k - число связности для вершин e_kE_i;

• _k - число связности для вершин e_kE_i.

П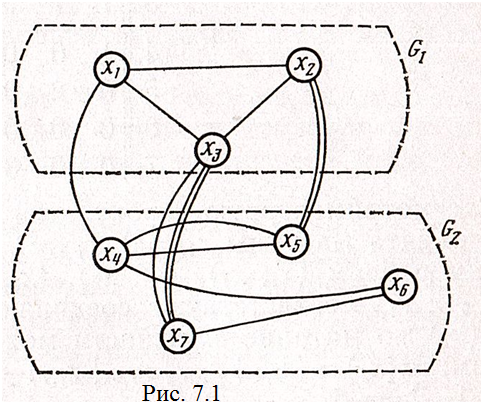 оясним понятие связности на примере графа G, разбитого на 2 части G₁ и G₂, приведенного на рис. 7.1. Тогда числа связности для вершин G₁ определяется следующим образом:

(x₁)=r₁(G₂)-r₁(G₁)=1-2=-1;

(x₂)=r₂(G₂)-r₂(G₁)=2-2=0;

(x₃)=r₃(G₂)-r₃(G₁)=3-2=1;

Числа связности для вершин G₂:

(x₄)=r₄(G₁)-r₄(G₂)=1-3=-2

(x₅)=r₅(G₁)-r₅(G₂)=2-2=0;

(x₆)=r₆(G₁)-r₆(G₂)=0-2=-2;

(x₇)=r₇(G₁)-r₇(G₂)=3-1=2;

Очевидно, что число связности может быть положительным, отрицательным или равным нулю. Физический смысл числа связности следующий. Например, (x₁)=-1 означает, что при перестановке вершины x₁ из G₁ в G₂ число ребер в сечении увеличится на 1. Значение (x₂)=0 говорит о том, что перестановка вершины x₂ из G₁ в G₂ оставит без изменения число соединительных ребер.

Рассмотрим теперь итерационный алгоритм с использованием матрицы смежности. Он основан на теореме:

Перестановка двух произвольных вершин e_kE_i и e_qE_i приводит к уменьшению числа соединительных ребер между кусками в случаях: