1.2 Метод наименьших квадратов
Для определения параметров модели тренда можно применять метод наименьших квадратов. Линию тренда добавляем в точечную диаграмму.
1.2.1 Линейный тренд
Для решения бизнес - задач чаще всего используются линейные тренды согласно рисунку 1 . Однако можно вычислять и выводить в диаграммах также нелинейные тренды нескольких типов.
Рисунок 1 - Линейный тренд
1.2.2 Логарифмический тренд
Логарифмические тренды используются для описания данных, близких к логарифмической кривой, т. е. когда данные быстро увеличиваются или уменьшаются, а затем изменение прекращается (данные не могут содержать нулевых или отрицательных значений). Данный тип тренда изображен на
рисунке 2.
Рисунок 2 - Логарифмический тренд
1.2.3 Степенной тренд
Степенные тренды используются, когда данные плавно увеличиваются с нарастающей скоростью (данные не могут содержать нулевых или отрицательных значений) в соответствии с рисунком 3.
Рисунок 3 - Степенной тренд
1.2.4 Экспоненциальный тренд
Экспоненциальные тренды используются для данных, значения которых увеличиваются или уменьшаются с быстро нарастающей скоростью (данные не могут содержать нулевых или отрицательных значений) в соответствии с рисунком 4.
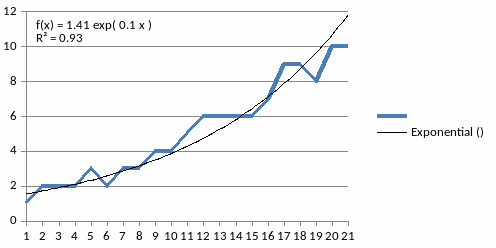
Рисунок 4 - Экспоненциальный тренд
1.2.5 Полиномиальный тренд
Полиномиальные тренды используются, если данные несколько раз изменяются вверх и вниз (устанавливаемый пользователем порядок полинома – от 2 до 6 – зависит от числа направлений изменения данных), т.е. полиноминальный тренд описывает данные, плавно изменяющиеся в разных направлениях. Уравнение полиноминального тренда зависит от порядка полинома.
Полиноминальный
тренд второго порядка (квадратичный
тренд) описывает данные, кривая графика
которых напоминает латинскую букву U
(или перевернутую U). Уравнение
полиноминального тренда второго порядка
имеет вид
,
изображен на рисунке 5.
Рисунок 5 - Полиномиальный тренд 2 степени
Полиноминальные
тренды высоких порядков могут описывать
данные, содержащие несколько максимумов
и минимумов. Уравнение полиноминального
тренда третьего порядка имеет вид
,
согласно рисункам 6-9.
Рисунок 6 - Полиномиальный тренд 3 степени
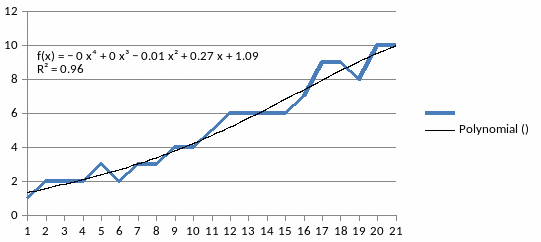
Рисунок 7 - Полиномиальный тренд 4 степени
Рисунок 8 - Полиномиальный тренд 5 степени
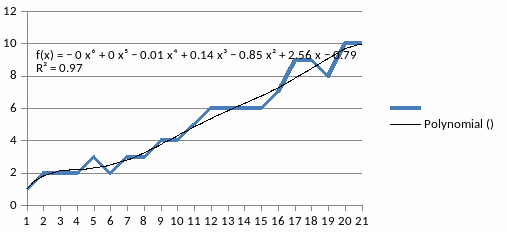
Рисунок 9 - Полиномиальный тренд 6 степени
Подобранные модели надо проверить на адекватность исходным данным.
2 Полиномиальная модель 2 степени
2.1
Для проверки модели надо найти модельные
значения, подставив в подобранную модель
y
= 0,0099x2
+ 0,232x
+ 1,0241 , R² = 0,9637 вместо
исходные значения времени
(1,2,…,21) и найти разности (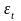
)
между исходными (таблица 1) и модельными
значениями уровней ряда динамики.
Результаты
расчета приведены в таблице 2.
Таблица 2 - Исходные, модельные значения уровней и остатки ряда динамики
T |
Исходные уровни yt |
Модальные значения |
Остатки |
Ϭmed |
1 |
1 |
1,266 |
-0,266 |
- |
2 |
2 |
1,5277 |
0,4723 |
+ |
3 |
2 |
1,8092 |
0,1908 |
+ |
4 |
2 |
2,1105 |
-0,1105 |
- |
5 |
3 |
2,4316 |
0,5684 |
+ |
6 |
2 |
2,7725 |
-0,7725 |
- |
7 |
3 |
3,1332 |
-0,1332 |
- |
8 |
3 |
3,5137 |
-0,5137 |
- |
9 |
4 |
3,914 |
0,086 |
+ |
10 |
4 |
4,3341 |
-0,3341 |
- |
11 |
5 |
4,774 |
0,226 |
+ |
12 |
6 |
5,2337 |
0,7663 |
+ |
13 |
6 |
5,7132 |
0,2868 |
+ |
14 |
6 |
6,2125 |
-0,2125 |
- |
15 |
6 |
6,7316 |
-0,7316 |
- |
16 |
7 |
7,2705 |
-0,2705 |
- |
17 |
9 |
7,8292 |
1,1708 |
+ |
18 |
9 |
8,4077 |
0,5923 |
+ |
19 |
8 |
9,006 |
-1,006 |
- |
20 |
10 |
9,6241 |
0,3759 |
+ |
21 |
10 |
10,262 |
-0,262 |
- |
Итого |
- |
- |
0,123 |
|
2.2
Для проверки случайности колебаний
уровней остаточной последовательности
будем
использовать критерий «серий»,
основанный на медиане выборки. Для
этого расположим уровни остаточной
последовательности
(таблица
3)
в порядке возрастания в вариационный
ряд. Находим в этом ряду медиану:
= - 0,111. Как видно из полученной
последовательности общее число «серий»
=
13; а протяженность самой длинной «серии»
Kmax
=3.
Таблица 3 - Уровни остаточной последовательности в порядке возрастания
Упорядоченные остатки |
Упорядоченные остатки |
-1,006 |
0,086 |
-0,7725 |
0,1908 |
-0,7316 |
0,226 |
-0,5137 |
0,2868 |
-0,3341 |
0,3759 |
-0,2705 |
0,4723 |
-0,266 |
0,5684 |
-0,262 |
0,5923 |
-0,2125 |
0,7663 |
-0,1332 |
1,1708 |
-0,1105 |
|
|
|
О качестве (точности) полученных моделей судят чаще всего по относительной средней ошибке аппроксимации:
(5)
Если
в пределах 8 -10%, то это говорит о хорошем
качестве (точности) уравнения тренда,
т.е. хорошем подборе модели к исходным
данным.
= 11,2%
(6)
Выборка признается случайной, если выполняются неравенства (6) для 5%-го уровня значимости. Подставив в неравенства (6) соответствующие значения переменных, получим:
kmax : 3 < 7,66332
(7)
𝜈 : 13 > 6,61731
Следовательно, ряд динамики ε отклонений от тренда состоит из случайных величин.
Проверка соответствия распределения случайной последовательности
остаточной
компоненты
нормальному закону распределения может
быть произведена лишь приближенно, так
как она является выборкой из генеральной
совокупности.
2.3 Рассчитаем выборочные коэффициенты асимметрии (АВ) и эксцесса (ЭВ) и их среднеквадратические ошибки:
Таблица 3 - Данные для расчетов центральных моментов
|
|
|
|
|
|
|
|
-0,272 |
0,074 |
-0,020 |
0,005 |
0,466 |
0,218 |
0,101 |
0,047 |
0,184 |
0,034 |
0,006 |
0,001 |
-0,116 |
0,014 |
-0,002 |
0,000 |
0,562 |
0,316 |
0,178 |
0,100 |
-0,778 |
0,606 |
-0,472 |
0,367 |
-0,139 |
0,019 |
-0,003 |
0,000 |
-0,520 |
0,270 |
-0,140 |
0,073 |
0,080 |
0,006 |
0,001 |
0,000 |
-0,340 |
0,116 |
-0,039 |
0,013 |
0,220 |
0,048 |
0,011 |
0,002 |
0,760 |
0,578 |
0,440 |
0,334 |
0,281 |
0,079 |
0,022 |
0,006 |
-0,218 |
0,048 |
-0,010 |
0,002 |
-0,737 |
0,543 |
-0,401 |
0,296 |
-0,276 |
0,076 |
-0,021 |
0,006 |
1,165 |
1,357 |
1,581 |
1,842 |
0,586 |
0,344 |
0,202 |
0,118 |
-1,012 |
1,024 |
-1,036 |
1,048 |
0,370 |
0,137 |
0,051 |
0,019 |
-0,268 |
0,072 |
-0,019 |
0,005 |
Итого |
5,980 |
0,429 |
4,287 |
|
0,0059 |
|
m2= |
0,285 |
Центральный момент второго порядка |
m3= |
0,020 |
Центральный момент третьего порядка |
m4= |
0,204 |
Центральный момент четвертого порядка |
=
|
|
|
Ав= |
0,1344 |
Выборочный коэффициент асимметрии |
Эв= |
-0,482 |
Выборочный коэффициент эксцесса |
ϬA= |
0,4647 |
Среднеквадратическая ошибка коэффициента асимметрии |
ϬЭ= |
0,7555 |
Среднеквадратическая ошибка коэффициента эксцесса |
|Ав| |
: 0,1344 |
< |
0,6967 |
|Эв+(6/(21+1))| |
: 0,2097 |
< |
1,1332 |
Так как система неравенств выполняется, то гипотеза о близости эмпирического распределения остатков ряда динамики к нормальному принимается.
2.4 Проверка независимости значений остаточной случайной последовательности, т.е. отсутствия существенной автокорреляции, осуществляется с помощью критерия Дарбина – Уотсона. Критерий Дарбина – Уотсона связан с гипотезой о существовании автокорреляции первого порядка, то есть автокорреляции между соседними остаточными членами ряда.
Таблица 4 - Данные для расчета критерия Дарбина – Уотсона
-
№
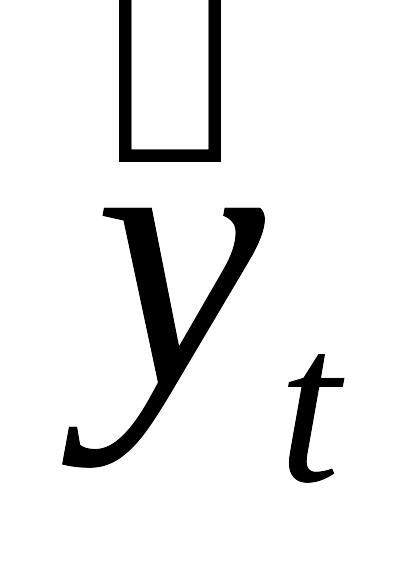
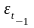
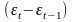
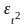
1
1,266
-0,266
-
-
-
0,070756
2
1,5277
0,4723
-0,266
0,7383
0,545087
0,22306729
3
1,8092
0,1908
0,4723
-0,2815
0,079242
0,03640464
4
2,1105
-0,1105
0,1908
-0,3013
0,090782
0,01221025
5
2,4316
0,5684
-0,1105
0,6789
0,460905
0,32307856
6
2,7725
-0,7725
0,5684
-1,3409
1,798013
0,59675625
7
3,1332
-0,1332
-0,7725
0,6393
0,408704
0,01774224
8
3,5137
-0,5137
-0,1332
-0,3805
0,14478
0,26388769
9
3,914
0,086
-0,5137
0,5997
0,35964
0,007396
10
4,3341
-0,3341
0,086
-0,4201
0,176484
0,11162281
11
4,774
0,226
-0,3341
0,5601
0,313712
0,051076
12
5,2337
0,7663
0,226
0,5403
0,291924
0,58721569
13
5,7132
0,2868
0,7663
-0,4795
0,22992
0,08225424
14
6,2125
-0,2125
0,2868
-0,4993
0,2493
0,04515625
15
6,7316
-0,7316
-0,2125
-0,5191
0,269465
0,53523856
16
7,2705
-0,2705
-0,7316
0,4611
0,212613
0,07317025
17
7,8292
1,1708
-0,2705
1,4413
2,077346
1,37077264
18
8,4077
0,5923
1,1708
-0,5785
0,334662
0,35081929
Продолжение таблицы 4
-
№
19
9,006
-1,006
0,5923
-1,5983
2,554563
1,012036
20
9,6241
0,3759
-1,006
1,3819
1,909648
0,14130081
21
10,262
-0,262
0,3759
-0,6379
0,406916
0,068644
итого
12,91371
5,98060546
При уровне значимости по таблицам значений критерия
Дарбина
- Уотсона можно определить при
и
(число факторов) критические значения
.
Получены
следующие промежутки внутри интервала
[0;4].
График?? Как подписать?
0
2,58
4
2,78
Нет оснований отклонять нулевую гипотезу, следовательно, автокорреляция отсутствует.
2.5
Проверку равенства математического
ожидания случайной остаточной
последовательности
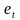нулю, распределенной по нормальному
закону, осуществим на основе
-
критерия Стьюдента.
tф= |
= 0,050298924 |
tкрит= |
2,085963441 |
|
|
tф<tкрит |
|
(8)
Получим, что 0,05 < 2,09 , т.е. есть основания при заданной доверительной вероятности отвергнуть гипотезу о равенстве нулю математического ожидания случайной остаточной последовательности, распределенной по нормальному закону.