
Раздел 15
Найти
общее решение уравнения:
![]() .
.
Найти
общее решение линейного неоднородного
дифференциального уравнения:
![]() .
.
Найти
общее решение линейного неоднородного
дифференциального уравнения:
![]() .
.
Найти
общее решение линейного неоднородного
дифференциального уравнения:
![]() .
.
Найти
общее решение уравнения:
![]() .
.
Раздел 16
Члены
ряда
![]() положительны и не возрастают, и f(x) –
такая непрерывная невозрастающая
функция, что
положительны и не возрастают, и f(x) –
такая непрерывная невозрастающая
функция, что
![]() .
Тогда если несобственный интеграл
.
Тогда если несобственный интеграл
![]() сходится, то
сходится, то
ряд расходится
ряд неабсолютно сходится
ряд абсолютно сходится
ряд сходится
ряд условно сходится
Радиус
сходимости
![]() степенного ряда
степенного ряда
![]() вычисляется по формуле:
вычисляется по формуле:
Ряд
![]() сходится тогда и только тогда, когда:
сходится тогда и только тогда, когда:
Ряд
![]() сходится тогда и только тогда, когда:
сходится тогда и только тогда, когда:
Пусть
дан ряд
![]() со строго положительными членами и
существует
со строго положительными членами и
существует
![]() .
Тогда данный ряд сходится при:
.
Тогда данный ряд сходится при:
Пусть
дан ряд
![]() со строго положительными членами и
существует
со строго положительными членами и
существует
![]() .
Тогда данный ряд сходится при:
.
Тогда данный ряд сходится при:
Степенной
ряд
![]() сходится для всех значений
сходится для всех значений
![]() ,
и его сумма равна:
,
и его сумма равна:
Степенной
ряд
![]() сходится для всех значений
сходится для всех значений
![]() ,
и его сумма равна:
,
и его сумма равна:
Степенной
ряд
![]() сходится для всех значений
,
и его сумма равна:
сходится для всех значений
,
и его сумма равна:
Степенной
ряд
![]() сходится при
сходится при
![]() ,
и его сумма равна:
,
и его сумма равна:
Степенной
ряд
![]() сходится при
сходится при
![]() ,
и его сумма равна:
,
и его сумма равна:
Степенной
ряд
![]() сходится при
сходится при
![]() ,
и его сумма равна:
,
и его сумма равна:
Ряд
![]() расходится тогда и только тогда, когда:
расходится тогда и только тогда, когда:
Ряд расходится тогда и только тогда, когда:
Пусть
дан ряд
со строго положительными членами и
существует
![]() .
Тогда данный ряд расходится при:
.
Тогда данный ряд расходится при:
Пусть
дан ряд
со строго положительными членами и
существует
![]() .
Тогда данный ряд расходится при:
.
Тогда данный ряд расходится при:
Укажите ряд Тейлора функции f (x) в окрестности точки x0.
Ряд называется сходящимся, если:
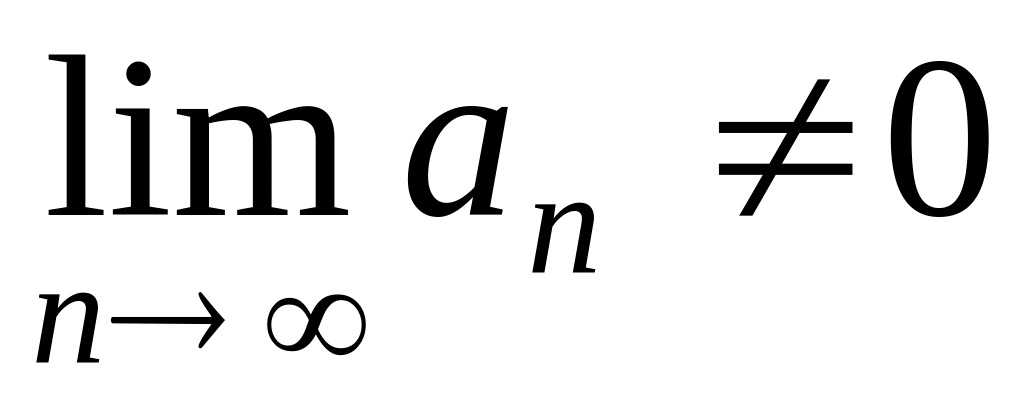
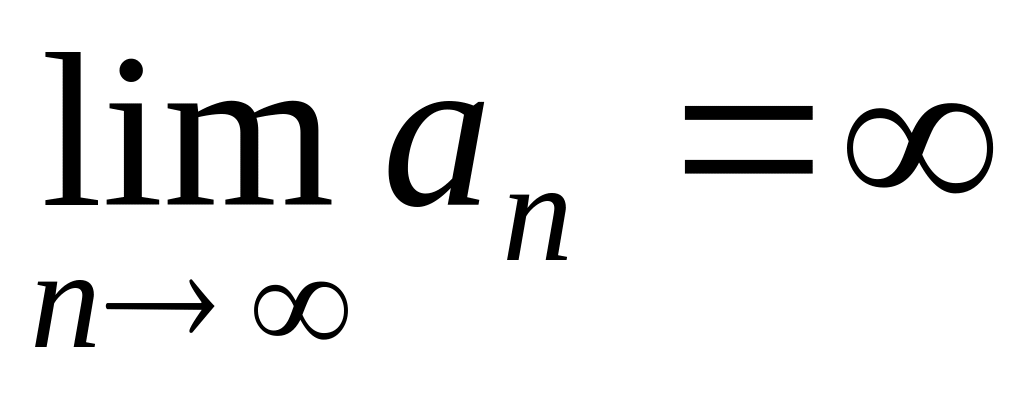
существует конечный предел частичной суммы, т.е.
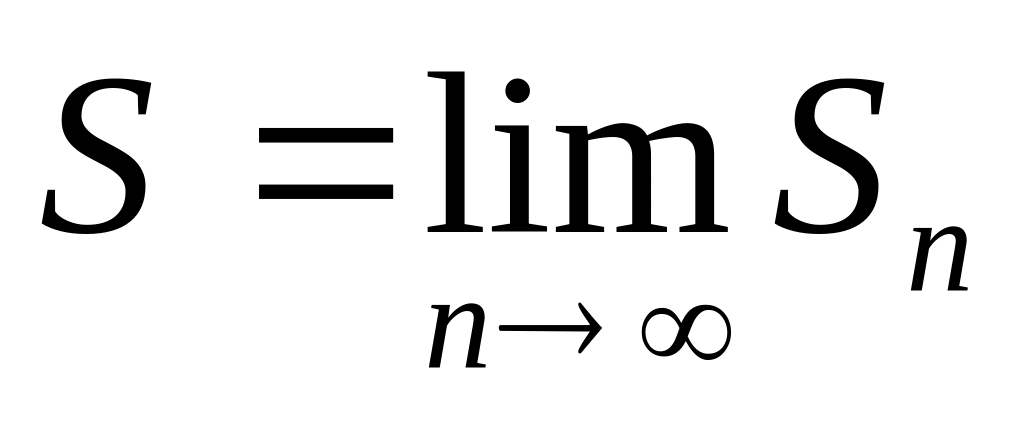
частичная сумма не ограничена

Знакоположительный
ряд
![]() будет
сходящимся, если при сравнении со
сходящимся знакоположительным рядом
будет
сходящимся, если при сравнении со
сходящимся знакоположительным рядом
![]() выполняется условие:
выполняется условие:
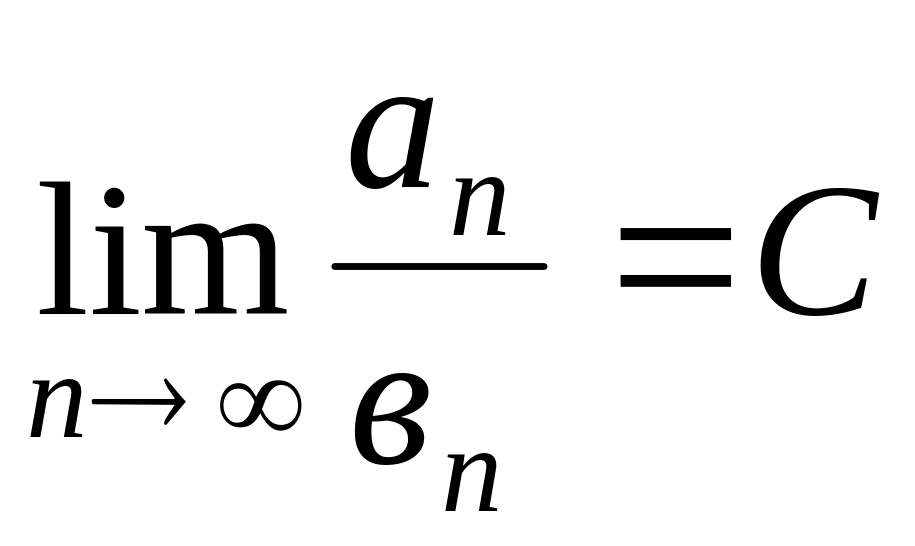 (С¹0)
(С¹0)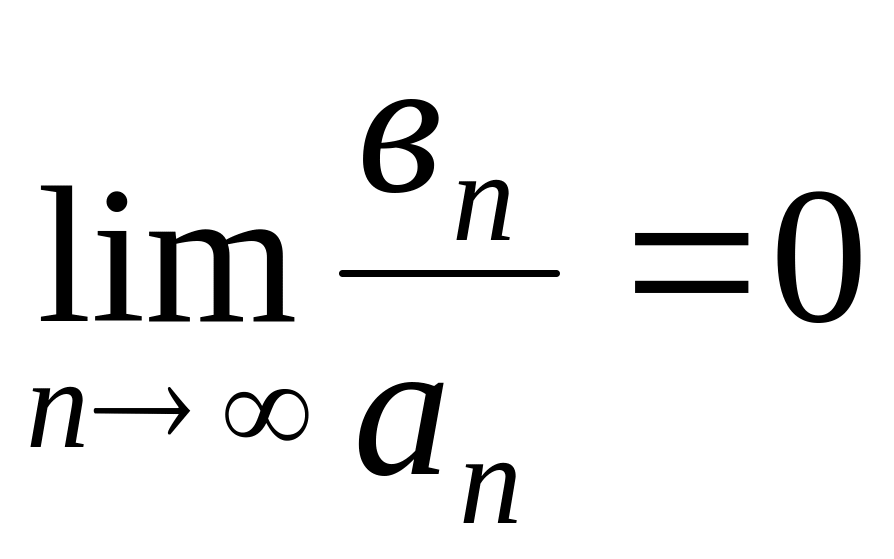



Какое условие является достаточным для расходимости ряда ?
Какое
условие является достаточным для
сходимости ряда
![]() ?
?
Какое
условие является необходимым для
сходимости ряда
![]() ?
?
Какое условие является достаточным для расходимости ряда ?
Положительный
ряд
![]() будет
сходящимся, если при сравнении со
сходящимся положительным рядом
будет
сходящимся, если при сравнении со
сходящимся положительным рядом
![]() выполняется условие
выполняется условие
Положительный ряд будет расходящимся, если при сравнении с расходящимся положительным рядом выполняется условие
