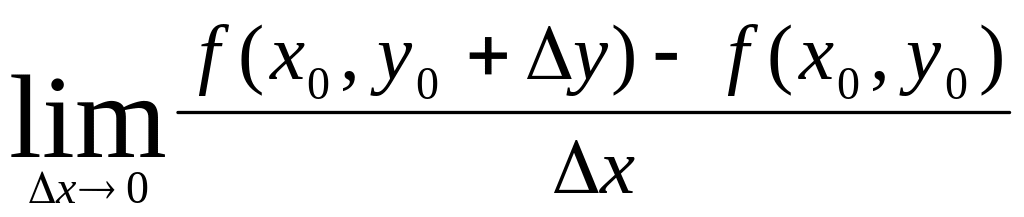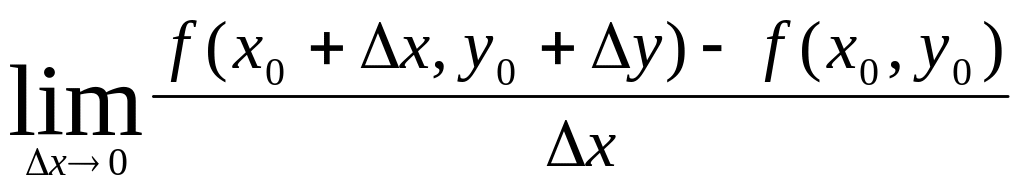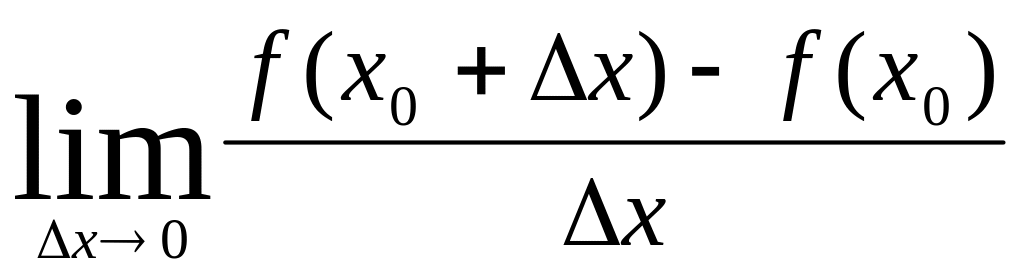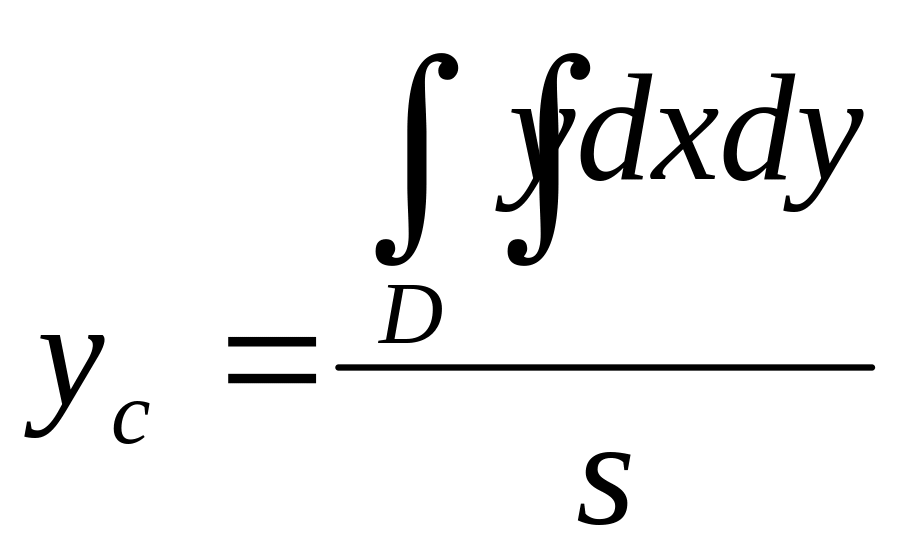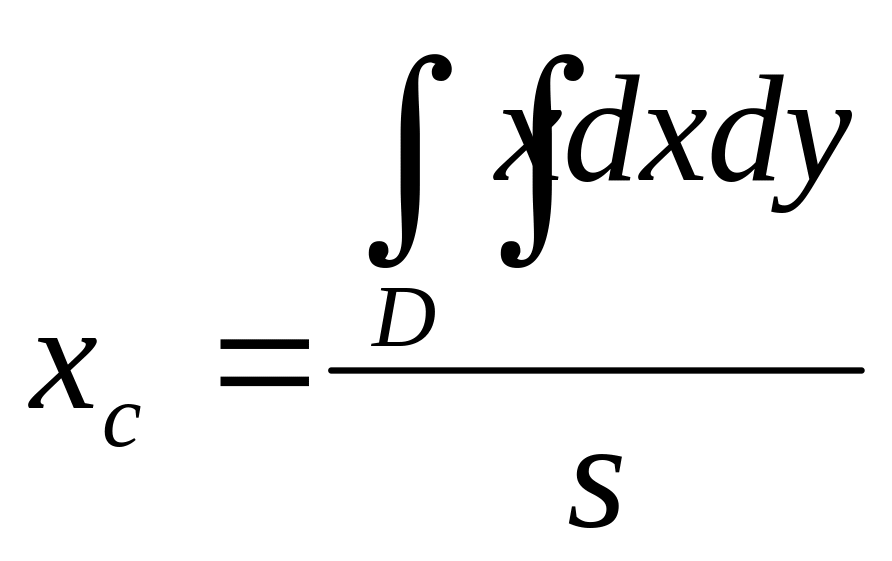Раздел 1

Площадь области в полярных координатах вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

При каком условии функция имеет максимум в стационарной точке , если , , ?

1. 

2. 

3. 

4. 

5. 

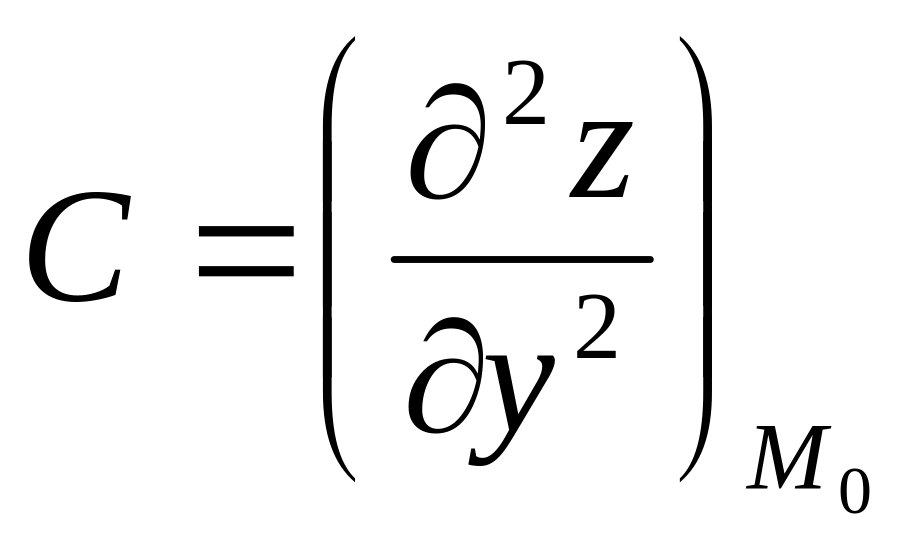При каком условии функция имеет минимум в стационарной точке , если , , ?

При каком условии функция не имеет экстремума в стационарной точке , если , , ?

1. 

2. 

3. 

5. 

При каком условии вопрос о наличии экстремума функции в стационарной точке М₀ остается открытым,

если , , ?

5. 

Что называется частной производной функции f(x, y) по переменной x в точке ?

1. 

2. 

3. 

4. 

5. 

Что называется частной производной функции f(x,y) по переменной у в точке ?

1. 

2. 

3. 

4. 

5. 

Что называется частным приращением функции f(x,y) по переменной x в точке ?

1. 

2. 

3. 

4. 

5. 

Что называется частным приращением функции f(x,y) по переменной y в точке ?

Какой вид имеет полное приращение функции f(x,y) в точке ?

4. 

Какой вид имеет полный дифференциал функции ?

1. 

2. 

3. 

4. 

5. 

Укажите формулу нахождения , если , , .

1. 

2. 

3. 

4. 

5. 

Укажите формулу для нахождения , если , , .

2. 

3. 

4. 

5. 

Укажите формулу нахождения , если функция задана неявно ?

1. 

2. 

3. 

4. 

5. 

Укажите формулу нахождения , если функция задана неявно ?

1. 

3. 

4. 

5. 

Если тело задано в форме параллелепипеда, то объем тела вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

Если -однородная пластинка с плотностью и площадью S , то ордината центра тяжести вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

Если - однородная пластинка с плотностью и площадью S , то абсцисса центра тяжести вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

Если - плотность тела , то масса тела вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

Если задано тело , то укажите формулу приведения к повторным интегралам тройного интеграла :

1. 

2. 

3. 

4. 

Если - плотность пластинки , то масса пластины вычисляется по формуле:

1. 

2. 

3. 

4. 

5. 

Если область - проекция тела на плоскости ОХУ, ограниченного сверху поверхностью , то его объем вычисляется с помощью двойного интеграла по формуле:

1. 

2. 

3. 

4. 

5. 

В декартовых координатах объем тела вычисляется по формуле:

1. 

2. 

3. 

4. 

В декартовых координатах площадь области вычисляется по формуле:

1. 

2. 

3. 

4. 

Указать в двойных интегралах формулу перехода к полярным координатам:

.

1. 

2. 

3. 

4. 

5. 

Раздел 2

Найти значение выражения для функции z = 3x³ - xy² - 2x²y в точке А(-1,-1).

1. 1

2. -6

3. 3

4. -1

5. 0

Найти значение выражения для функции в точке М₀(1,1).

1. 0

2. -1

3. -2

4. 1

5. 2

Найти значение выражения для функции в точке М₀(1,1).

1. 4

2. 0

3. -4

4. 1

5. -1

Найти значение выражения для функции в точке М₀(1,1).

1. 0

2. -2

3. 1

4. -1

5. 2

Найти значение выражения для функции в точке М₀(1,1).

1. 0

2. 1

3. 2

4. 4

5. 6