Земля как динамическая система
Древнегреческий математик и путешественник Пифагор ещё в VI веке до нашей эры заметил, что в южных странах видны созвездия, которых нет на северном небе. Двигаясь к северу, наблюдатель всё больше видит незаходящих звёзд. Во время лунных затмений тень Земли на лунном диске имеет круглую форму. Перечисленные факты послужили доказательством шарообразности Земли. Исаак Ньютон также знал это и считал, что форма Земли во многом зависит от центробежной силы, возникающей при осевом вращении небесного тела. Наша планета – почти шар, и об этом «почти» больше всего знают специалисты, изучающие геосферы.
«Превращение шарообразной Земли в субсферическое тело» началось во второй половине XVII века. Тогда было замечено, что часы с маятником, в Европе колеблющимся с частотой 1 раз в секунду, в районе экватора отстают. Специалисты французской академии, отправленные в Кайенну (фр. Гвиана), действительно установили, что регулированием длины маятника можно добиться неизменности хода часов, точнее – частоты качаний маятника, зависящей от силы тяжести. Было ясно, что это происходит вследствие разности расстояния от точки наблюдения до плотных масс центра планеты. Следовательно, Земля – не совсем шар. Ньютон и Гюйгенс пришли к подобному выводу теоретически, предположив, что изначально пластичная (или жидкая) планета приняла свою форму под действием центробежной силы. Позже методами триангуляционных измерений определили длину градуса меридиана в южных и северных широтах. Было установлено, что в Лапландии она составляет примерно 57437, а в Южной Америке (район перуанских Анд) – 56753 туаза [Неймар, 1902]. Если перевести полученные расстояния в метры, (1 туаз равен 1,949 м), то получится, что северный градус равен 111945 м, а южный – 110612 м. В России такими работами занималась с 1816 по 1855 год экспедиция под руководством В.Я. Струве и Тэннера. Но лишь Василию Яковлевичу Струве удалось довести работы до конца и вычислить сжатие сфероида, составившее 1:299,7. По этим данным увеличение длины дуги, соответствующей одному градусу на севере по отношению к южному району составляет 1200 м.
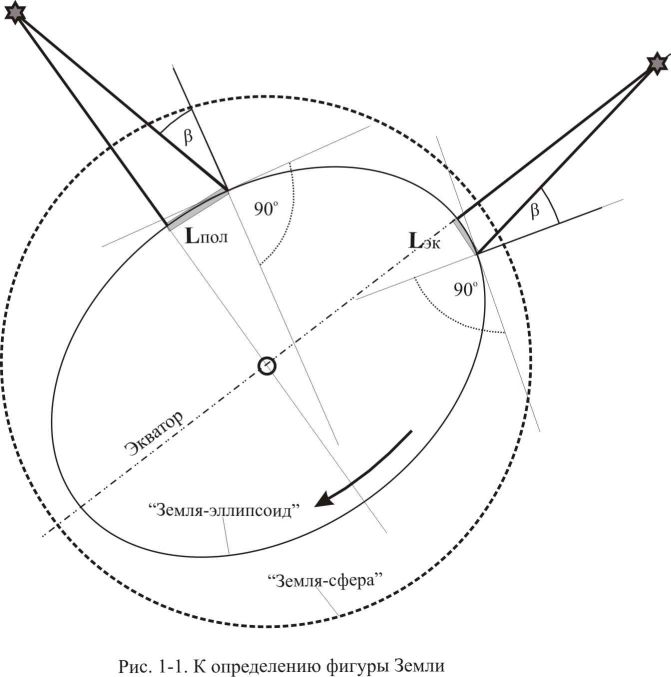
Французскими и российскими учёными были получены сходные результаты. Действительно, точки на поверхности планеты, фигурирующие в качестве реперов, где параллели с заданной широтой пересекают меридиан, определяются астрономогеодезическими методами. Разбивка меридиана в градусном делении представляет проведение неких условных отвесных лучей от поверхности планеты, в точках пересечений которых с меридианом и находятся наши реперы. Значит, длина дуги 1 градуса меридиана зависит от кривизны поверхности. Если бы мы могли измерить одинаковые углы, находясь в центре планеты, длина LЭК оказалось бы больше LПОЛ из-за влияния расстояния от центра Земли до дуги меридиана (рис. 1-1). Сплюснутость Земли у полюсов приводит к тому, что кривизна возрастает к экватору. Отвесные лучи в районе полюса, строящиеся по угловым измерениям на звёзды, будут пересекаться не в центре планеты, а дальше его. В районе экватора ситуация обратная. Значит, из-за кривизны поверхности расстояние, проходимое исследователем до получения нужного азимута на звезду, будет различным. В предельном случае – на плоскости это расстояние будет очень большим. Поэтому полученная разница примерно в 1250 м является доказательством того, что планета пока ещё сохраняет форму эллипсоида вращения.
С тех пор выполнено много измерений. Асимметричность Земли установлена достаточно надёжно. Южное полушарие оказалось более сжатым, и сейчас мы знаем, что планета имеет «грушевидную» форму (рис. 1-2). Экваториальное вздутие Земли достигает 21,4 км, а грушевидность обусловлена разницей длины полярных полуосей, достигающей 70-100 м [Мир географии…, 1984]. Радиусы, лежащие в экваториальной плоскости, также не совпадают по длине на 213 м. Максимальная глубина впадины в истинной фигуре Земли, выявленная у южной оконечности полуострова Индостан, достигает почти 120 м.
Истинная форма нашей планеты не соответствует ни сфере, ни эллипсоиду вращения, ни идеальной «груше», она более сложна. Это «геоид» – субсферическая масса, ограниченная поверхностью океанов в спокойном состоянии, продолженной мысленно под материками. В каждой точке геоида сила тяжести направлена по нормали к его поверхности. В настоящее время исследователи пользуются картами геоида, приведённого к эллипсоиду вращения со сжатием примерно 1:298,2. Рассчитать распределение силы тяжести для геоида мы не можем, поскольку аналитически геоид выразить нельзя, это фигура неправильная. Нормальные значения силы тяжести рассчитываются для трёхосного эллипсоида по формуле Гельмерта (1901-1909 гг.), поскольку последняя рассчитана для эллипсоида со сжатием 1:298.2, которое почти равно сжатию (α) эллипсоида Красовского (α = 1:298,3), принятого за эллипсоид относимости для всех геодезических работ в нашей стране. (Это значение сжатия близко к значению 1:298.6, выведенному по наблюдениям за движением искусственных спутников Земли).
Для чего мы приводим такие подробные сведения? Во-первых, для того чтобы максимально избежать неопределённостей, влияющих на результаты дальнейших выводов. Во-вторых, известно, что «фигура Земли определяется силой тяжести, основной компонентой которой является сила притяжения, так как по сравнению с ней влияние центробежной силы мало» [Миронов,1980]. О центробежной силе нельзя не говорить, ибо она характерна для любого криволинейного движения, а тем более для равномерного движения по окружности, представляющего, по мнению физиков, особый интерес. Известно, что «тело находится в состоянии покоя или равномерного прямолинейного движения, если на него не действуют иные силы, или равнодействующая этих сил равна нулю». В реальной ситуации мы имеем относительно равномерное движение почти по окружности, при котором силы в системе практически уравновешены. Значит, в системе с установившимся движением любые силы, нарушающие такую уравновешенность, должны почти отсутствовать. В первую очередь это относится к центробежной силе, якобы сильно влияющей на фигуру планеты.
Главным откликом на приложенную силу является ускорение. Направление изменения скорости (направление ускорения) соответствует направлению движения тела, являющегося источником силы. Приведённая классическая формулировка заставляет задуматься исследователя, наблюдающего столкновение бильярдных шаров. Чаще всего под воздействием импульса катящегося шара вначале неподвижный шар получает ускорение, направленное совсем не по направлению движения воздействующего объекта. Очевидно, во всех случаях взаимодействие невозможно без участия нескольких сил. В системе взаимодействуют исходный импульс, притяжение Земли и сила трения. Вообще, выражение «направление скорости» или «направление ускорения» следует отнести к неудачным терминам. Скорость как отношение расстояния к промежутку времени трудно представить в виде вектора. Векторной величиной является перемещение тела в выбранной системе координат.
В нашем случае центростремительное ускорение создаётся исключительно силами тяготения. Центробежная сила (и соответственно – ускорение) есть результат внешнего воздействия. Действительно, из физических справочников можно узнать, что центробежная сила представляет силу, «с которой движущаяся материальная точка действует на тело (связь), стесняющее свободу движения точки и вынуждающее её двигаться криволинейно». Из определения ясно, что центробежная сила вездесуща, поскольку любой объект движется в реальном веществе, стесняющем свободу его движения. Сразу становится понятным, что это и есть сила, возникающая при любом взаимодействии. Мы также знаем, что изменить момент инерции системы (главный момент количества движения относительно оси вращения) посредством только перераспределения взаимного расположения её частей невозможно [Физический энциклопедический словарь, 1984]. Повторим, что это происходит только под действием внешних сил. Значит, Земля при вращении взаимодействует с межпланетным веществом, а главное – испытывает гравитационное воздействие Солнца и других планет. Означенные внешние силы являются причиной изменения формы. Важными факторами при этом служат скорость вращения и плотность окружающего планету вещества. Даже при равномерном осевом вращении Земли некоторая часть энергии её движения теряется на взаимодействие с окружающим веществом в области верхних слоёв атмосферы, а также с изменяющимся притяжением Солнца. Расчёты интенсивности такого взаимодействия отсутствуют.
Из учебника по гравиразведке [Гравиразведка, 1990] запишем, что центробежная сила, возникающая вследствие суточного вращения Земли вокруг оси, пропорциональна расстоянию от оси вращения, массе и квадрату угловой скорости (ω) суточного вращения.
FЦ = mω2r.
Используем известную формулу Эйлера для кругового движения (υ=ωr) и получим, что
FЦ = mωυ, (1.1)
где υ – линейная скорость (максимальная на экваторе). Произведение массы на скорость представляет импульс тела, поэтому
FЦ = Рω. (1.2)
Мы получили, что центробежная сила, как сила взаимодействия изучаемого вращающегося тела с окружающей материей, зависит от импульса и угловой скорости его вращения. Для того чтобы показать реальность представления центробежной силы как результата взаимодействия, проведём ещё мысленный опыт с системой, обладающей движением вокруг оси. Так мы покажем, что не совсем корректно выглядят рассуждения о пустом пространстве, где «справедлива специальная теория относительности, где тела обладают инерцией, где во вращающейся системе есть силы Кориолиса и центробежные силы» [Новиков, 1990]. Николай и Андрей Грушинские убеждают нас, что если все звёзды вращаются, то «при сжатии звезды по законам физики должен сохраняться момент количества вращения» [Грушинский, 1985]. Значит, резкое уменьшение диаметра светила при коллапсе (в 100 000 раз) обязательно приведёт к увеличению во столько раз скорости осевого вращения. Предполагается зависимость не от внешних сил, а от радиуса, который не является материальной субстанцией.
Рассмотрим относительно изолированную жёсткую систему, в которой внешние воздействия отсутствуют, но изменяются размеры её составных частей с расположением относительно оси вращения. Пусть диск массой 1000 кг и диаметром 10 м вращается под действием начального импульса (Р) со скоростью 10 оборотов в секунду. Сконцентрируем те же 1000 кг на расстоянии не более 1 м от оси вращения и подумаем, изменится ли скорость вращения под воздействием такого же импульса (Р). Напомним, что все внешние воздействия по условию эксперимента отсутствуют. Очевидно, скорость не изменится. Ведь наша модель-система должна изменить динамику движения только благодаря существованию закона о постоянстве момента импульса. Но закон выведен из наблюдений за реальной динамикой системы, где истинное взаимодействие не всегда проявляется отчётливо. Кроме этого, из формулы (1.2) видно, что центробежная сила в такой жёсткой системе определяется одинаковой угловой скоростью для всех частей тела и общим импульсом.
В итоге, поставленный вопрос не выглядит однозначно решённым, и мы не можем уверенно судить, в какой степени осуществляется взаимодействие вращающейся планеты с окружающим веществом, с внешним полем тяготения и каков реальный вклад центробежных сил в формирование фигуры Земли. Поэтому во всех изданиях, посвящённых гравиметрии, 1800 мГал всегда списываются на особенности внутреннего строения планеты, зависящего от её эволюции. Именно это и скрыто от наблюдателя. Не исключается вариант, что современная форма Земли почти «безразлична» к действию центробежных сил в равномерно вращающейся системе и её форма действительно определяется силами движения-тяготения составных частей и особенностями динамической эволюции. «Если бы Земля была сплюснутым сфероидом в гидростатическом равновесии, f было бы 1/299.8, так что сжатие Земли несколько превышает величину, следующую из простой гидростатической модели» [Акасофу, Чепмен, 1974]. (Параметр f представляет отношение разности экваториального и полярного радиусов к экваториальному). Внешние силы, влияющие на динамику системы, более значительны для планеты как тела, движущегося по околосолнечной орбите со скоростью почти 30 км/с. (Детальнее особенности орбитального движения Земли рассмотрены в следующих разделах).
Перечислим наиболее примечательные характеристики нашей планеты.
1. Наличие сложной формы, больше всего похожей на неравномерно сплюснутую у полюсов сферу. Южной полярной области по отношению к северной соответствует отрицательная аномалия поверхности геоида амплитудой примерно 30-40 м [Грушинский, 1985].
2. Существование многих положительных и отрицательных аномалий истинной поверхности Земли, глубинность источников которых может составлять от нескольких сотен до 1200 км. Причиной формирования таких аномалий предполагается динамика взаимодействующих составных частей планеты.
3. Общее магнитное поле (ОМП) Земли соответствует полю магнитного диполя, ось которого развёрнута относительно оси вращения на угол примерно 11,5°. Вероятно, в далёком прошлом системе, уже обладающей ОМП, был сообщён импульс осевого вращения в плоскости, не перпендикулярной оси магнитного диполя.
4. Соотношение приполярных аномалий геоида и магнитных полюсов таково, что южный магнитный полюс расположен в краевой части отрицательной аномалии геоида, а северный – примерно на границе положительной и отрицательной аномалий.
Перечисленные характеристики не позволяют считать нашу планету сферически слоистым и достаточно однородным образованием и с полным основанием должны рассматриваться в качестве атрибутов закономерно и сложно устроенного космического тела, претерпевшего длительную эволюцию. Детали эволюции лучше всего проясняются при изучении динамики других тел Солнечной системы, на основе хорошо известных физических законов. Наиболее фундаментальным среди них является закон всемирного тяготения, надёжно установивший всеобщность взаимодействия для всех без исключения объектов Вселенной.
Рисунки к разделу 1
