3.6. Основные виды алгоритмов

Очевидно, что в зависимости от условий задач и исходных данных к ним алгоритмы решения этих задач будут различны. Однако можно выделить основные виды алгоритмов, используемых для решения простых задач. Эти простые алгоритмы и используются при составлении алгоритмов решения сложных задач. Основные виды простых алгоритмов будут пояснены ниже на соответствующих блок-схемах.

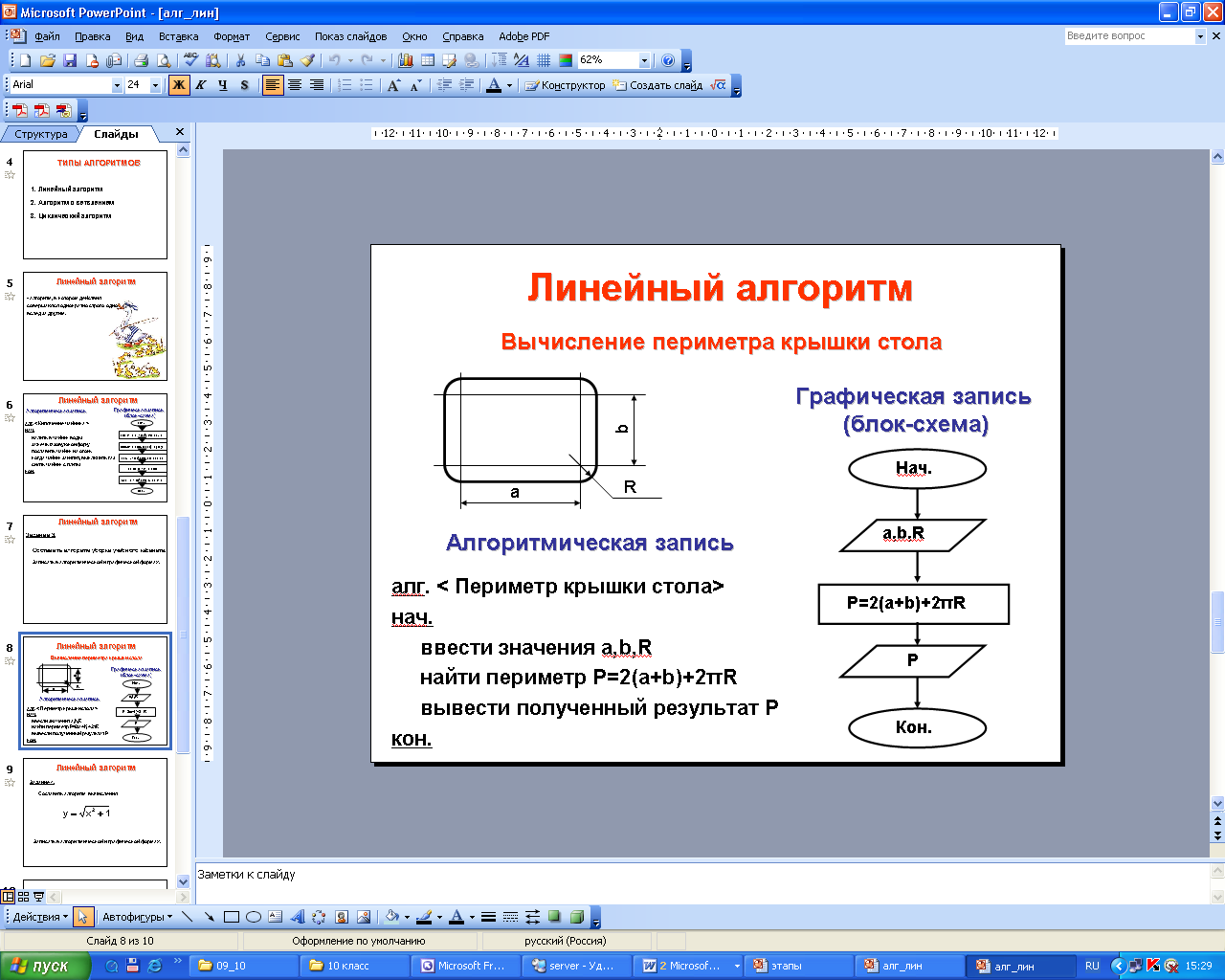
Линейный алгоритм

Алгоритм, в котором действия совершаются строго одно вслед за другим, называется ЛИНЕЙНЫМ.

Такими, например, будут алгоритмы вычислений по простейшим формулам: площадь круга, длина окружности, квадрат гипотенузы и т.д.

Для описания алгоритмов используют определенную форму записи - алгоритмический язык. Запись алгоритма должна оформляться по следующим правилам.

На первой строке записывается слово алгоритм или его трехбуквенное сокращение  алг. Далее за этим словом записывается название алгоритма.

На второй строке записывается слово начало или его сокращение  нач.

Далее в столбик записываются действия, составляющие алгоритм. Последней строкой описания алгоритма должно быть слово конец или  кон. в той же позиции, что и слово  начало. Общая форма записи:

алг. <название алгоритма>

нач. <составные команды>

действия

кон. <конец>

В алгоритмической форме можно записывать не только алгоритмы для вычислительных машин, но и различные инструкции, предписания и рекомендации для людей.

Например: инструкция по кипячению чайника в виде алгоритма, записанного на алгоритмическом языке и в виде блок-схем:

 алг. < Кипячение чайника.>

нач.

налить в чайник воды

зажечь газовую конфорку

поставить чайник на огонь

когда чайник закипит, выключить газ

снять чайник с плиты

кон.

Следующий пример линейного алгоритма:

Алгоритмическая структура «ветвление»

Легко и просто было бы жить, если бы удалось раз и навсегда расписать какие поступки, и в какой последовательности совершать. На самом деле нам постоянно приходится принимать решения в зависимости от создавшейся ситуации. Если идет дождь, то мы берем зонт. Если жарко, то идем купаться. Разумеется, встречаются более сложные ситуации, когда надо делать выбор.

Логику принятия любого решения можно описать тремя ключевыми словами:

ЕСЛИ <условие> ТО <действия 1> ИНАЧЕ <действия2> - полная форма

Иногда <действия 2> могут отсутствовать:

ЕСЛИ <условие> ТО <действия 1> - неполная форма

Например:

ЕСЛИ хочешь быть здоров, ТО закаляйся, ИНАЧЕ валяйся весь день на диване

ЕСЛИ низко ласточки летают, ТО будет дождь, ИНАЧЕ дождя не будет

ЕСЛИ назвался груздем, ТО полезай в кузов.

Форма организации алгоритма действий, при которой в зависимости от выполнения некоторого условия совершается та или иная последовательность действий, называется ветвлением.

Для обозначений ветвлений на блок-схемах используются ромбы, называемые блоками проверки условия.

Рассмотрим два примера.

1. Алгоритм покупки билетов в кино может выглядеть так:

1) подойти к кассе

2) если билеты на сеанс 18.00 имеются, то купить билеты

3) отойти от кассы

2. Алгоритм вечера выходного дня. Тогда:

1) если уроки выучены, то иди гулять,

2) иначе учи уроки.

Мы видим, что при выполнении каждого из этих алгоритмов наступает такой момент, когда появляется несколько направлений для продолжения.

Алгоритм как бы раздваивается, разветвляется. В этом случае говорят, что алгоритм содержит ветвление.

Алгоритмическая запись ветвления:

Ветвление в неполной форме: Ветвление в полной форме:

 если  <условие>   если  <условие>

то серия 1   то серия 1

 все    иначе серия 2

  все

Графическая форма записи (блок-схемы ветвления):

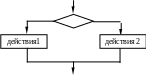
действия 1