ВСТУП
Виробнича функція (англ. production function, нім. Betriebs funktion f) - залежність кінцевого виходу продукції чи її вартості від використання різних факторів виробництва, конкретних видів ресурсів і затрат, подана в математичній формі. Як правило, застосовують прості функції з однією або кількома змінними - лінійну, квадратичну, степеневу, показникову, гіперболічну тощо.
Виробнича функція задає максимальний обсяг випуску (Q), який може виробити фірма для кожної специфічної комбінації вхідних ресурсів. В моделі поведінки фірми для спрощення аналізу ми будемо брати лише два ресурси для довгострокового періоду - працю (L) і капітал (К), і тільки один змінний фактор - працю - для короткострокового періоду.
Метод виробничої функції широко застосовують як в макро-, так і в мікроекономічному аналізі. В макроекономіці розраховують агрегатну функцію для кожної країни. Так, вчені П.Дуглас, Р.Солоу, Е.Денісон обчислювали функцію американського виробництва, Я. Тінберген здійснив відповідні розрахунки для Німеччини, Франції, Великобританії, США.
На мікрорівні існують тисячі функцій виробництва, тому що кожна фірма має свою виробничу функцію. Функції виробництва вказують на існування численних альтернативних можливостей одержання певного обсягу продукції за різних співвідношень між факторами виробництва.
Функцію виробництва реальної фірми можна визначити емпірично через виміри її фактичних показників. За допомогою такого аналізу фірма і приймає рішення про вибір технологічно ефективного способу виробництва.
Завдання
Метою роботи є визначення залежності між обсягом виробництва і величиною різних виробничих ресурсів, а саме чисельності робочої сили та основними засобами (капіталом) галузі.
З ймовірністю 0,95, використовуючи метод найменших квадратів:
оцінити параметри виробничої регресії Кобба-Дугласа, що має вигляд
;
оцінити адекватність побудованої моделі статистичним даним генеральної сукупності за допомогою критерію Фішера;
визначити частинні коефіцієнти еластичності та сумарний коефіцієнт еластичності;
визначити прогнозне значення та інтервал довіри для прогнозу;
побудувати ізокванти при у=у3 та у=у10.
Статистичні дані
-
Працезатрати (x1),
у.г.о.
Основні засоби (x2),
у.г.о.
Обсяг виготовленої продукції (y), у.г.о.
78,2
30,1
50,3
82,5
30,8
53,5
84
33,7
53,1
86,7
35,3
56,5
87
40,5
54,1
92,8
39,4
58,2
91,7
41,8
55,1
95,3
40,5
57,2
94,7
44,2
56,1
92,9
46
55,3
99,5
47,8
57,1
102,9
49,5
58,7
102,6
49,7
58,1
-
50,1
58,1
Виконання роботи
Оцінюємо параметри виробничої регресії Кобба-Дугласа, використовуючи метод найменших квадратів, за формулою
.
Z |
||
1 |
3,405 |
3,918 |
1 |
3,428 |
3,980 |
1 |
3,517 |
3,972 |
1 |
3,564 |
4,034 |
1 |
3,701 |
3,991 |
1 |
3,674 |
4,064 |
1 |
3,733 |
4,009 |
1 |
3,701 |
4,047 |
1 |
3,789 |
4,027 |
1 |
3,829 |
4,013 |
1 |
3,867 |
4,045 |
1 |
3,902 |
4,072 |
1 |
3,906 |
4,062 |
ZT |
||||||||||||
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
3,404525 |
3,404525 |
3,427515 |
3,517498 |
3,56388296 |
3,7013 |
3,6737658 |
3,732896 |
3,701302 |
3,788725 |
3,828641 |
3,867026 |
3,906005 |
3,966511 |
3,918005 |
3,979682 |
3,972177 |
4,03424064 |
3,99083 |
4,0638854 |
4,00915 |
4,046554 |
4,027136 |
4,012773 |
4,044804 |
4,062166 |
ZTZ |
||
13 |
48,01506 |
52,2338457 |
48,01506 |
177,6921 |
192,99328 |
52,23385 |
192,9933 |
209,898283 |
(ZTZ)-1 |
||
1167,073 |
57,43607 |
-343,24 |
57,43607 |
6,953107 |
-20,6863 |
-343,24 |
-20,68626 |
104,4413 |
ZT
|
58,68424 |
216,9116 |
235,8324 |
b0 = |
0,23438 |
a1 = |
0,31251 |
a2 = |
0,77789 |
Перевіряємо
отримані результати
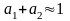
0,31251 + 0,77789 = 1,0904