3.2.7 Ізотерма адсорбції Фрейндліха

Задовго до робіт Ленгмюра Фрейндліх експериментально знайшов залежність величини адсорбції від концентрації чи тиску:

і ,

де – рівноважний тиск; – рівноважна концентрація; – сталі, які знаходять експериментально.

Часто адсорбцію виражають відношенням молів адсорбтива до маси адсорбента:

.

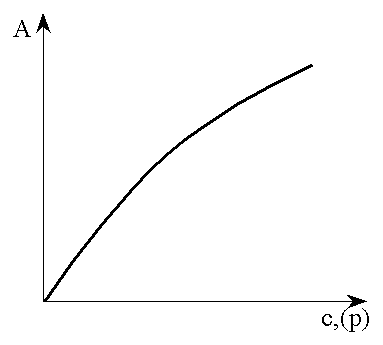
Ізотерма адсорбції Фрейндліха має вигляд кривої і представлена на рис.3.15.

Вираз рівняння Фрейндліха через рівноважну концентрацію придатний як для адсорбції газів, так і для адсорбції розчинів.

Рівняння ізотерми адсорбції Фрейндліха можна вивести, якщо прийняти, що адсорбція не обмежується мономолекулярним шаром і кількість адсорбованої речовини необмежено зростає із збільшенням тиску чи концентрації. Наступним припущенням було, що поверхня адсорбента неоднорідна і що адсорбція на кожному із типів активних центрів підпорядковується рівнянню Ленгмюра. Крім того, Фрейндліх припускав, що між адсорбованими молекулами існує взаємодія.

Сталі і коливаються в широких межах. Їх фізичний зміст стає зрозумілим, якщо прийняти або , тоді і являють собою величину адсорбції при рівноважних тиску 1 Па або концентрації 1 моль/дм³. Показники і є правильними дробами і характеризують ступінь наближення ізотерми до прямої, тому з підвищенням температури сталі і повинні зменшуватися, а і збільшуватися. При і рівняння Фрейндліха перетворюється в рівняння Генрі. Горизонтальна прямолінійна ділянка ізотерми, що відповідає високим тискам або концентраціям ( в рівнянні Ленгмюра), може бути одержана тільки при і . Таким чином, показники і по суті повинні бути самі функціями тиску чи концентрації. А оскільки і приймаються сталими в межах 0,2–1,0 для адсорбції із газового середовища і може приймати значення 0,1–0,5 для адсорбції із розчинів, рівняння Фрейндліха придатне тільки для інтервалу середніх тисків або концентрацій.

Для практичного використання рівняння Фрейндліха логарифмують і одержують рівняння прямої, представленої на рис. 3.16:

, .

Рисунок 3.15 − Ізотерма адсорбції Фрейндліха

Рисунок 3.16 − Логарифмічна форма ізотерми адсорбції Фрейндліха

Точка перетину прямої з лінією ординат дає значення або , тангенс кута нахилу до осі абсцис дає значення чи .

Недоліком теорії адсорбції Фрейндліха є те, що вона незадовільно пояснює дані фізичної адсорбції. Наприклад, було знайдено, що при уявному насиченні поверхні адсорбованою речовиною виявилась покритою тільки мала частка загальної площі адсорбента. Крім того, гранична адсорбція не залишається сталою, а збільшується при зниженні температури.

3.2.8 Рівняння бет (Брунауера,Еммета,Теллера)

Слід зазначити, що перші спроби одержати рівняння ізотерми полімолекулярної адсорбції були зроблені ще Ленгмюром. Сучасна ж форма рівняння полімолекулярної адсорбції – основного рівняння узагальненої теорії Ленгмюра – була запропонована пізніше Брунауером, Емметтом і Теллером (так звана теорія БЕТ).

1. На поверхні адсорбента є певне число рівноцінних в енергетичному відношенні активних центрів.

2. Взаємодія сусідніх адсорбованих шарів, першого і останнього, відсутня.

3. Кожна адсорбована молекула нижнього шару являє собою можливий активний центр для адсорбції молекул верхнього адсорбційного шару.

4. Молекули в другому, третьому й наступних шарах ведуть себе як молекули рідини.

Відомо, що при значному тиску газ переходить в пароподібний стан, а останній при досягненні тиску, що дорівнює тискові насичення , конденсується. При цьому і адсорбція парів рідини, що змочує поверхню адсорбента, стає нескінченно великою. Отже, якщо в області тисків, далеких від насичення, ріст адсорбції сповільнюється, то з подальшим підвищенням тиску і наближенням до адсорбція починає зростати і, врешті-решт, досягає значної величини. Адсорбційний шар при цьому потовщується, адсорбція стає полімолекулярною. При досягненні наступає об’ємна конденсація.

П ри виводі рівняння адсорбції БЕТ приймемо, що при адсорбції парів адсорбовані на уже зайнятих місцях молекули не покидають їх негайно, але утворюються кратні адсорбційні шари, подібні до картини, зображеної на рис. 3.17. В міру наближення до число вільних місць скорочується, число місць, зайнятих одношаровими комплексами спочатку зростає, а потім за рахунок утворення двошарових комплексів спадає.

Розглянемо полімолекулярну адсорбцію як серію квазіхімічних реакцій утворення двошарових і кратношарових комплексів:

пара	+	поверхня адсорбента		одношарові комплекси
пара	+	одношарові комплекси		двошарові комплекси	і т.д.

Якщо – частки вільної поверхні, а , і т.д. – частки поверхні, зайняті одношаровими, двошаровими і т.д. комплексами, то загальна величина адсорбції з урахуванням кратності кожного комплексу буде дорівнювати

, (3.7)

а сталі рівноваги відповідних процесів будуть виражатися так:

, , і т.д. (3.8)

У зв’язку з тим, що взаємодія адсорбента дуже залежить від відстані молекул адсорбата від поверхні адсорбента та значно зменшується зі збільшенням сталих і , хоч і не дорівнюють одна одній, але різниця між ними значно менша від різниці між і . Тому для наближеного опису полімолекулярної адсорбції можна прийняти

,

де – стала рівноваги між насиченою парою і рідиною, яка +дорівнює .

В цьому випадку із рівняння (3.8) випливає

; ; і т.д.

Підставляючи ці вирази в рівняння (3.6), отримаємо

. (3.9)

Сума часток заповнення

. (3.10)

Оскільки вираз у квадратних дужках є спадною геометричною прогресією, то сума її членів дорівнює

. (3.11)

З другого боку, ряд, вміщений у квадратні дужки рівняння (3.10), являє собою похідну ряду по , тому

. (3.12)

Підставивши рівняння (3.11) в рівняння (3.8), отримаємо

. (3.13)

З другого боку з рівнянь (3.9) і (3.11) випливає

.

Підставивши цей вираз у рівняння (3.12), отримаємо

. (3.14)

Прийнявши та позначивши , отримаємо кінцевий вираз рівняння полімолекулярної адсорбції БЕТ

. (3.15)

Прийнявши (приведений або відносний тиск пари) будемо мати

.

Подібно до сталої рівноваги для хімічних реакцій, стала адсорбційної рівноваги пов’язана з енергією Гіббса рівнянням

.

Потенціюючи це рівняння, отримаємо

,

де – так званий ентропійний множник;

.