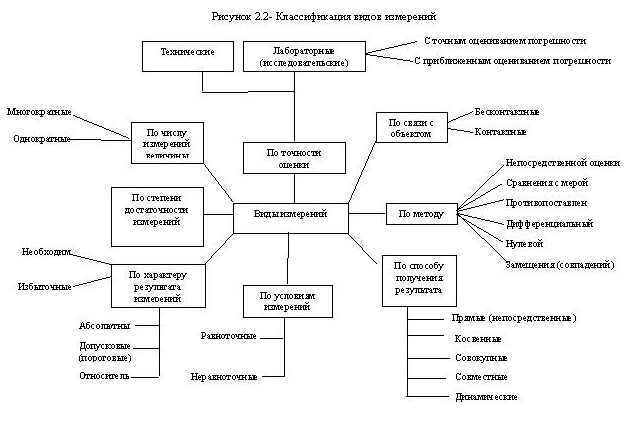
2.2 Виды и методы измерений

Классификация видов измерений приведена на рисунке 2.2. Виды измерений определяются физическим характером измеряемой величины, требуемой точностью измерения, необходимой скоростью измерения, условиями и режимом измерений и т. д. Из рисунка 2.2 следует, что в метрологии существует множество видов измерений и число их постоянно увеличивается. Можно, например, выделить виды измерений в зависимости от их цели: контрольные, диагностические и прогностические, лабораторные и технические, эта­лонные и поверочные, абсолютные и относительные и т.д.

Наиболее часто используются прямые измерения, состоящие в том, что искомое значение величины находят из опытных данных путем экспериментального сравнения. Например, длину измеряют непосредственно линейкой, температуру - термометром, силу - динамометром. Уравнение прямого измерения: у = C∙х, где С — цена деления СИ.

Если искомое значение величины находят на основании известной зависимости между этой величиной и величинами, найденными прямыми измерениями, то этот вид измерений называют косвенным. Например, объем параллелепипеда находят путем умножения трех линейных величин (длины, ширины и высоты); электрическое сопротивление — путем деления падения напряжения на величину силы электрического тока. Уравнение косвенного измерения , где х - i-й результат прямого измерения.

Совокупные измерения осуществляются путем одновременного измерения нескольких одноименных величин, при которых искомое значение находят решением системы уравнений, получаемых в результате прямых измерений различных сочетаний этих величин. При определении взаимоиндуктивности катушки М, например, используют два метода: сложения и вычитания полей. Если индуктивность одной из них L₁, а другой - L₂, то находят L₀₁ = L₁ + L₂ + 2M и L₀₁ = L₁ + L₂ - 2M. Откуда M = (L₀₁ - L₀₂)/4.

Совместными называют производимые одновременно (прямые и косвенные) измерения двух или нескольких неодноименных величин. Целью этих измерений, по существу, является нахождение функциональной связи между величинами. Например, измерение сопротивления R_t проводника при фиксированной температуре t по формуле

,

где и — сопротивление при известной температуре t_о (обычно 20⁰С) и температурный коэффициент — величины постоянные, измеренные косвенным методом; - разность температур; t-заданное значение температуры, измеряемое прямым методом.

П

Сравнения с мерой

риведенные виды измерений включают различные методы, т. е. способы решения измерительной задачи с теоретическим обоснованием и разработкой использования СИ по принятой МВИ. Методика — это технология выполнения измерений с целью наилучшей реализации метода.

Прямые измерения — основа более сложных измерений, и поэтому целесообразно рассмотреть методы прямых измерений. В соответствии с РМГ 29—99 различают:

1. Метод непосредственной оценки, при котором значение величины определяют непосредственно по отсчетному устройству измерительного прибора, например измерение давления пружинным манометром, массы — на весах, силы электрического тока — амперметром.

2. Метод сравнения с мерой, где измеряемую величину сравнивают с величиной, воспроизводимой мерой. Например, измерение массы на рычажных весах с уравновешиванием гирей; измерение напряжения постоянного тока на компенсаторе сравнением с ЭДС параллельного элемента.

3. Метод дополнения, если значение измеряемой величины дополняется мерой этой же величины с таким расчетом, чтобы на прибор сравнения воздействовала их сумма, равная заранее заданному значению.

4. Дифференциальный метод характеризуется измерением разности между измеряемой величиной и известной величиной, воспроизводимой мерой. Метод позволяет получить результат высокой точности при использовании относительно грубых средств измерения.

5. Нулевой метод аналогичен дифференциальному, но разность между измеряемой величиной и мерой сводится к нулю. При этом нулевой метод имеет то преимущество, что мера может быть во много раз меньше измеряемой величины.

6. Метод замещения — метод сравнения с мерой, в которой измеряемую величину замещают известной величиной, воспроизводимой мерой. Например, взвешивание с поочередным помещением измеряемой массы и гирь на одну и ту же чашку весов.

Кроме того, можно выделить нестандартизованные методы:

• метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения. Например, измерения массы на равноплечих весах с помещением измеряемой массы и уравновешивающих ее гирь на двух чашках весов;

• метод совпадений, где разность между сравниваемыми величинами измеряют, используя совпадение отметок шкал или периодических сигналов.

Например, при измерении длины штангенциркулем наблюдают совпадение отметок на шкалах штангенциркуля и нониуса; при измерении частоты вращения стробоскопом — метки на вращающемся объекте с момента вспышек известной частоты.

В литературе [2; 43; 18] иногда встречается название измерений с однократными наблюдениями — обыкновенные измерения, а с многократными — статистические. Кроме того, если весь измеряемый параметр фиксируется непосредственно СИ, то это — абсолютный метод, а если СИ фиксирует лишь отклонение параметра от установочного значения, то это относительный (пороговый) метод измерения.

Другие виды и методы измерений (см. рисунок 2.2) не требуют специальных пояснений и будут рассмотрены ниже.