2.5.2 Динамические измерения и погрешности детерминированных линейных измерительных цепей

Для расчетно-экспериментального определения динамических характеристик используют типовые воздействия на вход ИП, которым соответствуют определенные реакции (отклики) на выходе ИП. В качестве типовых воздействий могут быть:

1. Единичная ступенчатая функция, представляющая собой мгновенные изменения величины на единицу.

Реакция h(t) на этот сигнал, называемая переходной характеристикой, воспроизводит скачок x(t) либо с запаздыванием, либо с колебанием и запаздыванием.

2. Импульсная (весовая) функция (δ-функция Дирака), равная нулю при t ≠ 0 и бесконечности - при t = 0, но ее площадь равна единице, так как 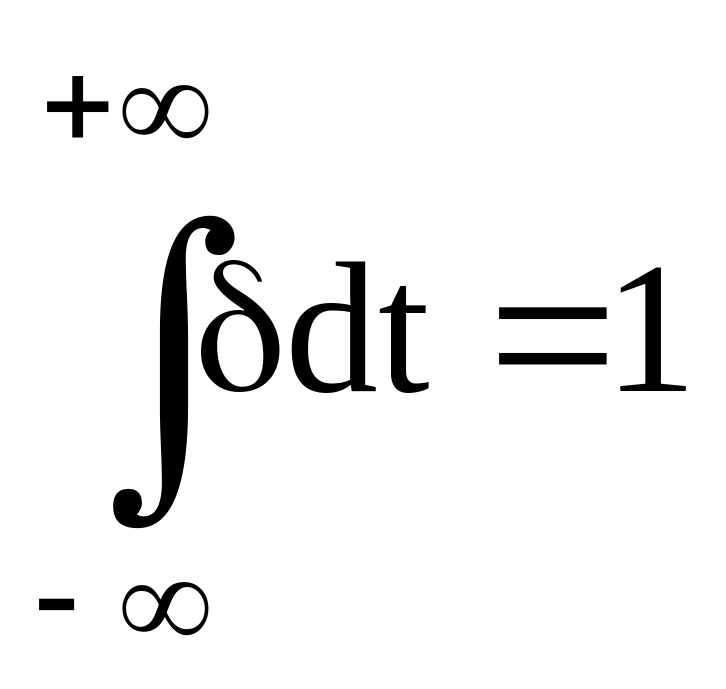. Реакция на импульсное воздействие - переходная характеристика g(t).

3. Линейно-измеряющееся во времени воздействие (рамповая функция)

Реакция на это воздействие - переходная характеристика с(t).

2. Синусоидальная (гармоническая) функция x(t) = A·sinωt. Реакция на это воздействие - сигнал y(t) со сдвигом по фазе на ω, который может быть и несинусоидальным. При изменении угловой частоты ω от 0 до ∞ можно получить амплитудно-фазовую частотную характеристику (АФХ), которая позволяет судить о статических и динамических свойствах ИП в частотной области. Характеристики h(t), g(t) и с (t) позволяют говорить об этих свойствах во временной области. В комплексном виде АФХ

(2.34)

где Р(ω) и jθ(ω) - действительная и мнимая части уравнения; X(jω) и Y(jω) - преобразование Фурье входного воздействия и реакции объекта на нее; A(ω) - амплитудно-частотная характеристика; φ(ω) - фазовая частотная характеристика (ФЧХ).

Другими словами, АЧХ и ФЧХ представляет оператор В в комплексной форме, где АЧХ — модуль, а ФЧХ — аргумент.

Перечисленные динамические характеристики для линейных (линеаризированных) сигналов взаимосвязаны, и при наличии одной из них можно получить другие. Например, АЧХ может быть получена, если известны переходные характеристики от ступенчатой или импульсной функции h(t) и g(t) по уравнениям

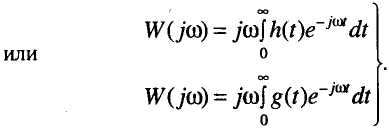(2.35)

В свою очередь,

и т.д.

Все ИП могут иметь различные динамические характеристики, но большинство из них с некоторыми допущениями можно отнести к одному из типовых звеньев: безынерционному (усилительному), апериодическому, колебательному, дифференцирующему и интегрирующему или их комбинациям. Все эти звенья имеют различные, но типовые для звена передаточные функции - комплексную величину, полностью определяющую динамику передачи измерительной информации.

Используя преобразования Лапласа, динамическую характеристику (2.34) можно представить при нулевых начальных условиях в виде передаточной функции

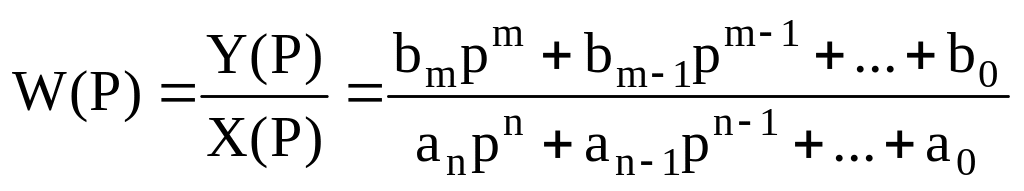, (2.36)

где Y(P) и Х(Р) - изображения по Лапласу выходного и входного сигналов; Р — комплексный параметр.

По передаточной функции W(P) определяют реакцию ИП на изменение входного сигнала.

Разнообразные звенья измерительной цепи могут быть соединены между собой различным образом, что влияет на передаточную функцию ИП в целом. В таблице 2.2 приведены соответствующие типовые передаточные функции основных звеньев для различных схем соединения.

Таблица 2.2 - Передаточные функции типовых звеньев

Звено	Передаточная функция W(P)	Схема соединения звеньев	Передаточная функция W(P)
Безынерционное (усилительное)	К	Последовательное соединение звеньев
Идеальное дифференцирующее	Кр
Реальное дифференцирующее		Параллельное соединение звеньев
Идеальное интегрирующее	К/р
Реальное интегрирующее		Встречно-параллельное соединение двух звеньев с обратной связью
Апериодическое (инерционное)
Колебательное		Замкнутая система

Примечание. К— коэффициент усиления; Т— постоянная времени; ξ - коэффициент успокоения (демпфирования); знак "+" при положительной, а "-" при отрицательной обратной связи; W_з(P) и W_p(P) - соответственно передаточные функции замкнутой и разомкнутой систем.

В общем случае для расчета динамической погрешности по уравнению (2.32) можно использовать формулу

. (2.37)

Коэффициенты С_о, С₁, ..., С_r называются коэффициентами ошибок. Их можно вычислить через передаточную функцию W(P). Для этого, считая в уравнениях (2.35) P = jω = 0 , W(0) = получаем C₀ = W(0) -1.

Дифференцируя (2.35) по Р и считая Р = 0, находим

.

Переходя к изображениям, получим

Δ_g(Р) = Y(P)-X(P) = X(P)[W(P)-l],

где W(P)-1 есть передаточная функция ИП по погрешности.