Метод приведенного градиента

Основная идея градиентных методов.

Наибольшее распространение получили методы возможных направлений.

Рис.(э.3).

В исходной точке Х₀ рассматривается несколько направлений (рис. э.3) для перехода в новую точку Х₁. Возможными называют направления, которые ведут в сторону уменьшения целевой функции (направления 1 и 4). Перемещение допускается по любому возможному направлению в текущей точке пропорционально некоторой константе t, называемой шагом, т.е.

. (3.5)

В точке Х₁ аналогично выбирается возможное направление и делается очередной шаг. Общее уравнение итерационного процесса по методу возможных направлений

. (3.6)

Величина шага влияет на сходимость вычислительного процесса, определяемую числом итераций: при малых t – процесс сходится, но медленно; при больших t – процесс может расходиться.

Между этими крайностями существует оптимальный шаг, который на принятом направлении приводит в точку максимального значения F, где это направление касается линии (рис. э.4)

Рис.э.4

Для отыскания оптимального шага можно на принятом направлении выражение подставить в целевую функцию и после преобразований получить новую функцию, зависящую только от шага , а затем найти ее минимальное значение.

В математике известно правило определения производных с учетом неявновыраженных функций.

Запишем исходную задачу с учётом разделения исходного вектора неизвестных на составляющие и :

(3.29)

Запишем производную с учетом неявной зависимости

, (3.30)

где производные в скобках определяются с учетом явной зависимости от и .

Производную найдем из ограничения , которое в результате дифференцирования определяет условие

, (3.31)

позволяющее получить

(3.32)

Здесь – квадратная матрица ( ), для которой существует обратная .

После подстановки (3.32) в (3.30) получим

.

Полученный градиент , составляющие которого определяются независимыми переменными, и называется приведённым градиентом.

Этот градиент может использоваться в процедуре градиентного метода:

(3.34)

Геометрически приведённый градиент является проекцией градиента на поверхность ограничений, а точнее – на плоскость, касательную нелинейной поверхности в текущей точке (рис. 3.17).

Рис.э.3

В точке условного минимума функции равен 0.

Решим пример 1.

Воспользуемся формулой (3.33) для приведенного градиента

В качестве свободной переменной примем . Тогда зависимой будет , и пользуясь (*.3) получаем .

В решаемой задаче х₁ является составляющей , а относится к . С учетом этого

.

	(*.9)

С учетом этого приведенный градиент

Основное уравнение градиентного метода

Рис.э.4

Решим пример1, взяв в качестве точности вычислений ε равное 0,01. В качестве исходного приближения примем

=0

Все расчеты приведены на рис. рис.э.5-э.10. Приближенные значения и содержатся в интервале ячеек В3:С13. Значения приведенного градиента содержатся в интервале ячеек D3:D13. Шаг (величина) изменения равная содержатся в интервале ячеек F3:F13. Значения целевой функции – величины дохода записаны в интервале ячеек G3:G13. Модуль приведенного градиента с каждым шагом уменьшается от 420 в стартовый момент, до 0.04 на 10 шаге (рис.э.6), что свидетельствует о правильном движении найденных приближений в сторону экстремума функции.. Таблица содержит 11 строк ( =0,1,2,..10), поскольку на 10 шаге модуль приведенного градиент стал равен 0.04, что меньше заданной точности вычислений ε ( 0.01). Приближенные значения =69.9927 =80.0073 содержатся в ячейках В13 и С13 соответственно. Отличие от решения, полученного аналитическими методами, составило менее 0,01. Обратите внимание, как происходит стабилизация значений , и с ростом , т.е. значения в соседних строках отличаются все меньше и меньше. Этот факт также проиллюстрирован графиком на рис.э.7.

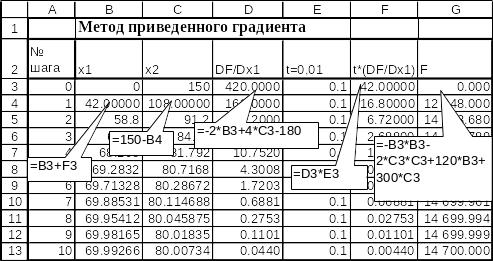
Рис.э.5

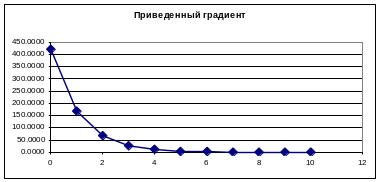
Рис.э.6

Рис.э.7

Рис.э. 8

Решение в MS Excel (надстройка «Поиск решения»).

Описать!

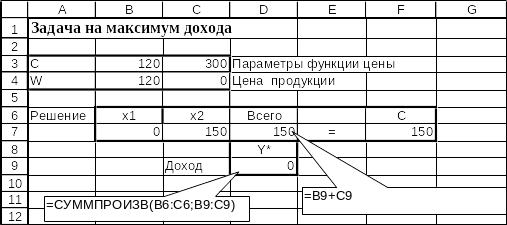
Рис.э.3. Фрагмент электронных таблиц Excel в режиме отображения данных.

Рис.э.4. Диалоговое окно надстройки «Поиск решения» при поиске оптимального решения.

Рис.э.4. Диалоговое окно надстройки «Поиск решения» при поиске оптимального решения.

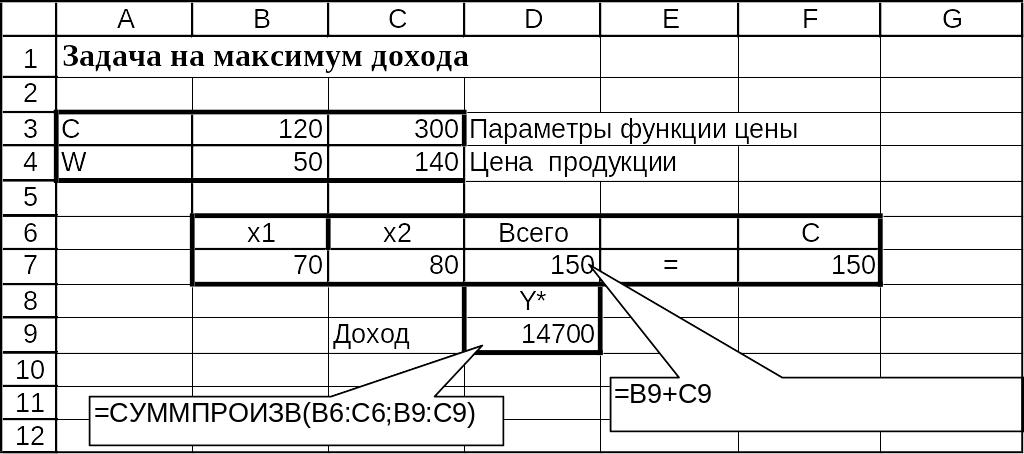
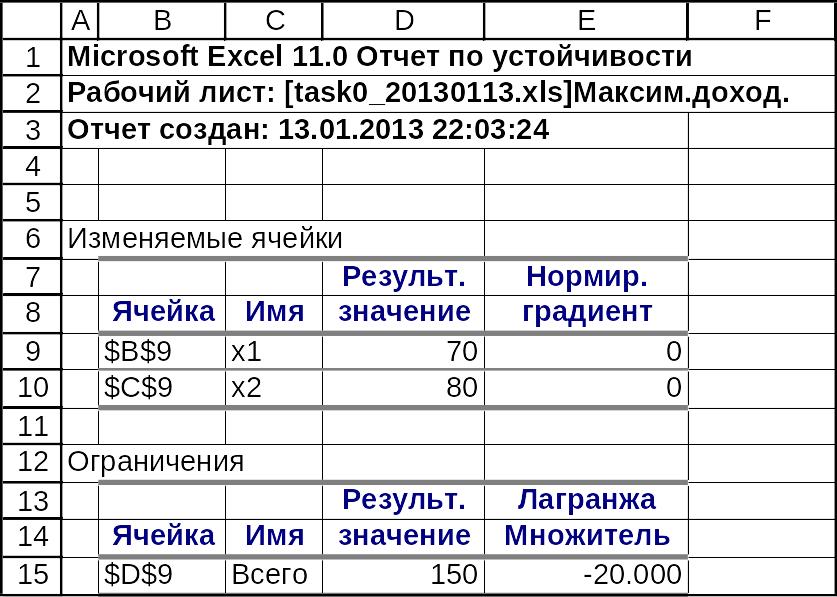
Рис э.5. Фрагмент электронных таблиц Excel с отчетом по устойчивости

Экономическая интерпретация множителей Лагранжа

Множитель Лагранжа – это двойственная переменная. Как и в линейном программировании, она показывает, на сколько изменится ЦФ при изменении правой части ограничений на единицу.

В рассмотренном примере . Следует ожидать, что при увеличении суммарного объема производимой продукции с 150 до 151 доход уменьшится на 20.

Проверим этот вывод. Пусть в нашей задаче критерий остался прежним, поменялась правая часть ограничения

.

Решим эту задачу в MS Excel (надстройка «Поиск решения»).

Рис.э.6. Фрагмент электронных таблиц MS Excel в режиме отображения данных.

Стационарная точка ,

Приращение критерия

Приращение функции -20,67 оказалось больше по модулю, чем ожидаемое приращение -20. Это объясняется нелинейностью целевой функции и тем, что множитель Лагранжа отражает приращение функции только при бесконечно малом приращении аргумента.

Иллюстрация полученного решения в MS Excel.

Чтобы проиллюстрировать полученное решение диаграммами с помощью линий уровня, затабулируем соответствующие функции (рис.э.7). Основную идея -описать решение кв.ур-я. Соответствующая диаграмма приведена на рис.*.10. Эта диаграмма является упрощенным вариантом рис.э.2. Точка соответствующая оптимальным значениям выделена. В ней линия уровня, соответствующая уровню =14 700 и линия равных объемов С=150 касаются и следовательно градиенты коллинеарны. Стрелки градиентов при самостоятельном решении можно нанести любым способом, в т.ч. вручную. На эту диаграмму нанести значения приближений к решению, полученные мтодом приведенного градиента.

Рис.э.7. Фрагмент электронных таблиц Excel в режиме отображения данных. Табулирование целевой функций для построения линий уровня.

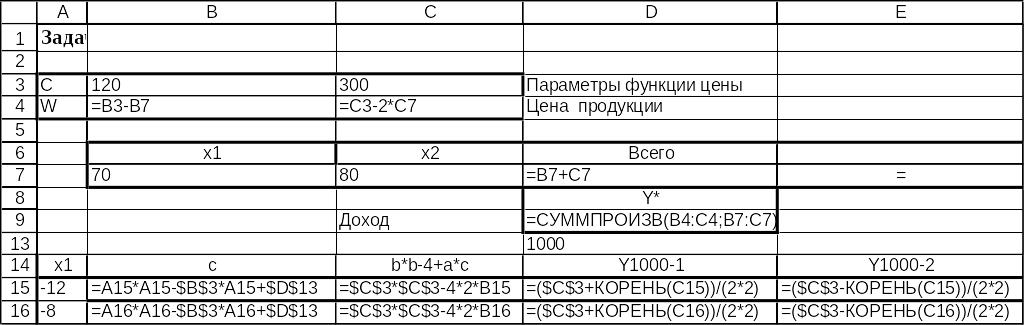
Рис.э.8. Фрагмент электронных таблиц Excel в режиме отображения формул. Табулирование целевой функций для построения линий уровня.

Чтобы построить семейство линий уровня или , при разных С заметим, что линии уровня - вложенные (концентрические) эллипсы.

Рассмотрим процесс построения линии при С =1000. Необходимо построить таблицу значений - .Для этого явно выразим через , используя соотношение или

Последнее соотношение следует рассматривать как квадратное уравнение относительно : , где . Значения с находится в интервале B15:B58. Значения дискриминанта находится в интервале C15:C58. Квадратное уравнение (при положительном дискриминанте) имеет два корня, это обеспечивает задание верхней и нижней ветвей эллипса. Первый корень находится в интервале D15:D58. Второй корень находится в интервале E15:E58. Построение диаграммы, у которой значения абсциссы лежит в интервале А15:А58, а ординаты в интервале D15:D58, обеспечивает вывод верхней дуги эллипса. Построение диаграммы, у которой значения абсциссы лежит в интервале А15:А58 , а ординаты в интервале E15:E58, обеспечивает вывод нижней дуги эллипса, Другие лини уровня строятся аналогично.

Рис.э.9. Линии уровня целевой функции и равного объема.

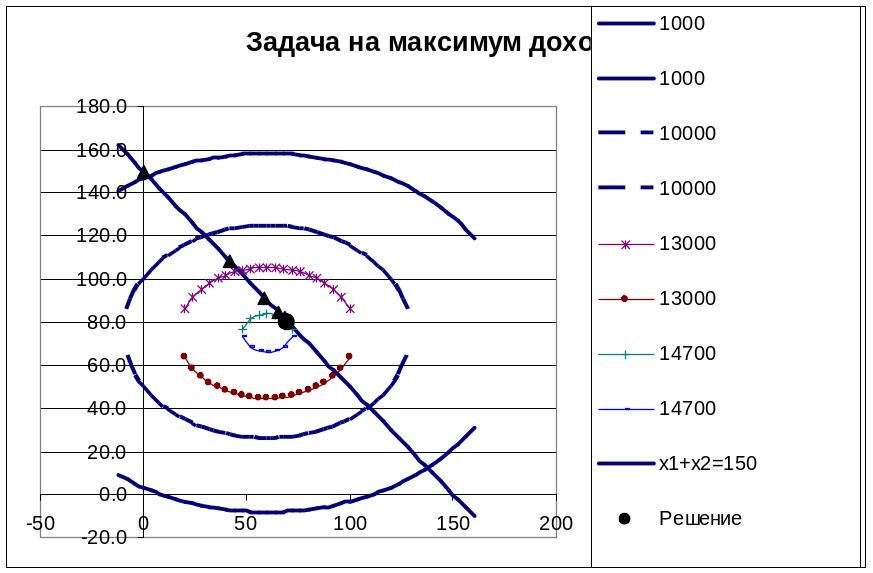Рис.э.10. Линии уровня целевой функции и равного объема. Маркеры треугольники показывают значения приближений к решению, полученные методом приведенного градиента.

Задача на максимум дохода.

Пример: Предприятие выпускает два вида продукции в объемах . Они реализуются по ценам соответственно. По плану предприятие должно выпустить ровно С единиц продукции. Определить план производства, обеспечивающий наибольший доход.

Параметры , В, a, b и C определяются по таблице в соответствии с номером варианта.

Задачу решить четырьмя способами:

1. Методом прямой оптимизации;

2. Аналитически, используя функцию Лагранжа;

3. Методом приведенного градиента;

4. Пользуясь надстройкой «Поиск решения» MS Excel.

Сравнить значения в оптимальной точке функции Лагранжа и «Множитель Лагранжа» из отчета по устойчивости надстройки «Поиск решения».

Увеличить параметр С на единицу. Снова решить задачу, пользуясь надстройкой «Поиск решения» MS Excel. Сравнить полученное значение дохода с базисным .

Проиллюстрировать полученное решение диаграммами, построив линии уровня соответствующие не менее трех уровней, например, и линию равного объема. Уровни округлить до ближайших «красивых значений» (кратных 5 или 10). На этой диаграмме построить градиенты к линиям уровня и к линии равного объема в оптимальной точке (можно вручную!).

№	С	А	В	a	b
1	180	340	140	2,5	1,3
2	175	335	135	2,4	1,2
3	170	330	130	2,3	1,1
4	165	325	125	2,2	1,0
5	160	320	120	2,1	1,3
6	155	315	140	2,0	1,2
7	150	310	135	1,9	1,1
8	170	305	130	2,5	1,0
9	180	300	125	2,4	1,3
10	190	295	120	2,3	1,2
11	200	290	140	2,2	1,1
12	140	285	135	2,1	1,0
13	130	280	130	2,0	1,3
14	120	275	125	1,9	1,2
15	110	270	120	2,5	1,1
16	100	265	140	2,4	1,0
17	160	340	135	2,3	1,3
18	170	335	130	2,2	1,2
19	180	330	125	2,1	1,1
20	190	325	120	2,0	1,0
21	200	320	140	1,9	1,3
22	140	315	135	2,5	1,2
23	130	310	130	2,4	1,1
24	120	305	125	2,3	1,0
25	110	300	120	2,2	1,3
26	100	295	140	2,1	1,2
27	160	290	135	2,0	1,1
28	170	285	130	1,9	1,0
29	180	280	125	2,1	1,3
30	190	275	120	2,0	1,2
31	200	270	125	1,9	1,1

Библиографический список

1. Булатов Б.Г., МЕТОДЫ ИССЛЕДОВАНИЯ ОПЕРАЦИЙ, Текст лекций

22