
- •Содержание
- •Лабораторная работа №1
- •1. Основные сведения
- •2. Порядок выполнения работы
- •3. Контрольные вопросы
- •4. Содержание отчета
- •Лабораторная работа №2
- •1. Основные сведения
- •2. Порядок выполнения работы
- •3. Контрольные вопросы
- •4. Содержание отчета
- •1. Основные сведения
- •2. Порядок выполнения работы
- •3. Контрольные вопросы
- •4. Содержание отчета
- •Лабораторная работа № 4
- •Основные сведения
- •Описание исследуемой системы
- •Порядок выполнения лабораторной работы
- •Контрольные вопросы
- •Содержание отчета
- •Литература
Описание исследуемой системы
Рассмотрим уравнение, описывающие динамику маятника с трением (рис. 4.8), совершающего свободные колебания относительно оси О:
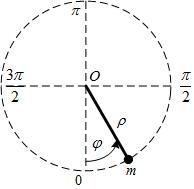
Рис. 4.8. Физический маятник
![]() , (4.5)
, (4.5)
где J- момент инерции маятника, kс – коэффициент трения, m – масса маятника, ρ – длина нити, φ(t) – угол отклонения маятника от вертикали, отсчитываемый из нижнего положения в направлении против часовой стрелки.
Перейдем
к уравнениям состояния вида (4.1), введя
переменные состояния в форме
![]() ;
;
![]() .
.
Тогда уравнение (4.5) станет:
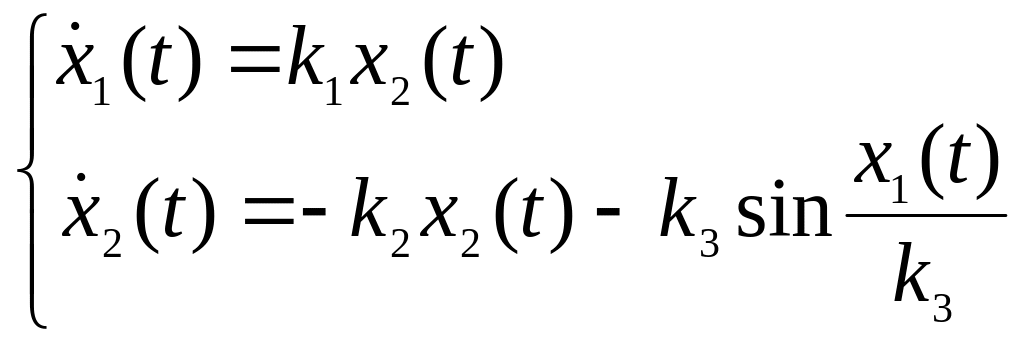 , (4.6)
, (4.6)
где k2=kc/J; k3=mgρ/J.
Фазовый портрет для системы (4.6) изображен на рис 4.9 (случай k1=1).
Очевидно,
что точками равновесия при k1=1,
т.е. значениями х*1
и х*2,
обращающими в ноль правые части уравнений
(4.6), являются точки
![]() ,
,
![]() Точки равновесия (0,0), (2π,0), (-2π,0) и т.д.
соответствуют нижней точке равновесия
(0,0). Траектории в окрестности этой точки
равновесия демонстрируют качественное
поведение, характерное для траекторий
в окрестности устойчивого фокуса. Точки
равновесия (π,0), (-π,0) и т.д. соответствуют
верхней точке равновесия маятника. В
окрестности этой точки поведение
траекторий характерно для фазового
портрета типа «седло». Устойчивые
траектории седловых точек (π,0) и (-π,0)
образуют сепаратрисы, которые отделяют
области, характеризующиеся тем, что все
траектории, начинающиеся внутри этих
областей, стремятся к точке равновесия
(0,0). Эта картина периодически повторяется.
Тот факт, что траектории могут стремиться
к различным точкам равновесии, объясняется
тем, что маятник может совершить несколько
полных оборотов, прежде чем он установится
в нижнем положении равновесия. Например,
траектории, начинающиеся в точках Аи В
(рис. 4.9) имеют одно и то же начальное
состояние, но разные начальные скорости:
траектория, начинающаяся в В имеет
бóльшую кинетическую энергию и совершает
полный оборот, прежде чем начать
осциллировать с убывающей амплитудой.
Точки равновесия (0,0), (2π,0), (-2π,0) и т.д.
соответствуют нижней точке равновесия
(0,0). Траектории в окрестности этой точки
равновесия демонстрируют качественное
поведение, характерное для траекторий
в окрестности устойчивого фокуса. Точки
равновесия (π,0), (-π,0) и т.д. соответствуют
верхней точке равновесия маятника. В
окрестности этой точки поведение
траекторий характерно для фазового
портрета типа «седло». Устойчивые
траектории седловых точек (π,0) и (-π,0)
образуют сепаратрисы, которые отделяют
области, характеризующиеся тем, что все
траектории, начинающиеся внутри этих
областей, стремятся к точке равновесия
(0,0). Эта картина периодически повторяется.
Тот факт, что траектории могут стремиться
к различным точкам равновесии, объясняется
тем, что маятник может совершить несколько
полных оборотов, прежде чем он установится
в нижнем положении равновесия. Например,
траектории, начинающиеся в точках Аи В
(рис. 4.9) имеют одно и то же начальное
состояние, но разные начальные скорости:
траектория, начинающаяся в В имеет
бóльшую кинетическую энергию и совершает
полный оборот, прежде чем начать
осциллировать с убывающей амплитудой.
Качественное поведение нелинейной системы может быть теоретически определено посредством ее линеаризации в окрестности точки равновесия х*=(х*1, х*2), если правые части системы (4.1) f1=(х1, х2) и f2=(х1,х2) непрерывно дифференцируемые функции.
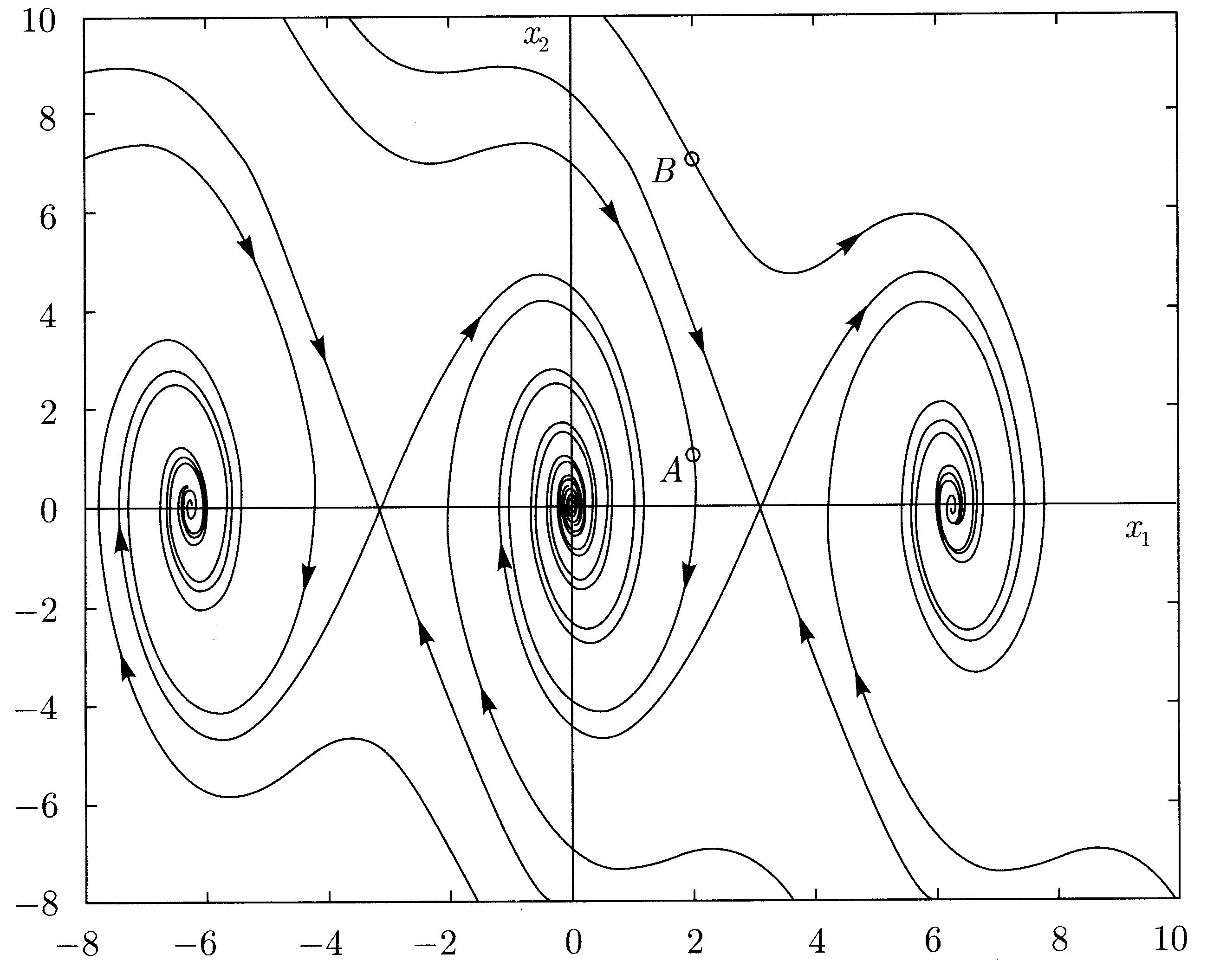
Рис. 4.9. Фазовый портрет маятника для системы (4.6)
Линеаризованная модель для системы (4.1) имеет вид:
![]() (4.7)
(4.7)
где y1=x1-x*1; y2=x2-x*2 – отклонения переменных x1 и x2 от положения равновесия;
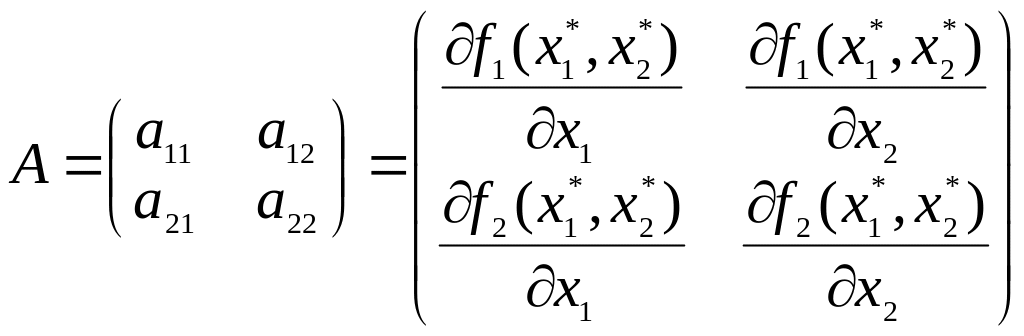 . (4.8)
. (4.8)
Матрица
![]() называется якобианом (матрицей Якоби)
функции f(x) в точке х=х*.
называется якобианом (матрицей Якоби)
функции f(x) в точке х=х*.
Если корни характеристического уравнения линеаризованной модели
det(pI2-A)=0
(р – оператор Лапласа, I2 – единичная матрица 2-го порядка)
не является чисто мнимыми, то о поведении исходной нелинейной системы (4.1) в окрестности положения равновесия х=х* можно судить по линеаризованной модели (4.7). Очевидно, что для системы (4.6) матрица Якоби имеет вид
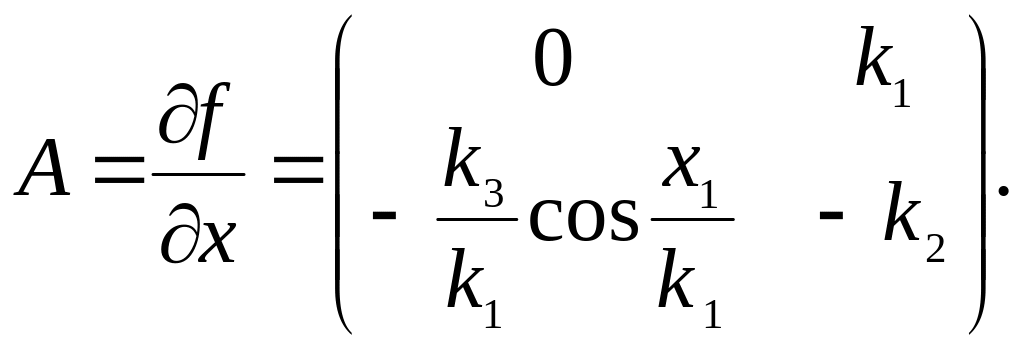
Поясним фазовый портрет, представленный на рис 4.9, при k1=1, k2=1, k3=2. Тогда
![]()
Очевидно, что в центре координат при х*1=0, х*2=0 матрица А
![]() ;
det(pI2-A1)=р2+р+2,
;
det(pI2-A1)=р2+р+2,
и
корни характеристического уравнения
![]() - два комплексно сопряженных корня с
отрицательной вещественной частью. Это
соответствует особой точке типа
устойчивого фокуса (рис. 4.2,б).
- два комплексно сопряженных корня с
отрицательной вещественной частью. Это
соответствует особой точке типа
устойчивого фокуса (рис. 4.2,б).
В
положении равновесия х*1=π,
х*2=0
имеем cosх*1=-1,
и матрица А имеет вид
![]() ;
det(pI2-A1)=р2+р-2,
;
det(pI2-A1)=р2+р-2,
корни характеристического уравнения соответственно равны λ1=1; λ2=-2. Как указывалось ранее, при наличии одного вещественного положительного корня положение равновесия является седловой точкой (рис. 4.5).
