Лабораторная работа № 4

Исследование динамики линейных и нелинейных САУ с помощью метода фазовой плоскости

Цель работы. Построение фазовых портретов линейных и нелинейных САУ с помощью компьютерного моделирования и их анализ при варьировании параметров системы.

1. Основные сведения

Метод фазовой плоскости применяют для исследования динамики систем второго порядка (n=2), заданных дифференциальными уравнениями в свободном состоянии

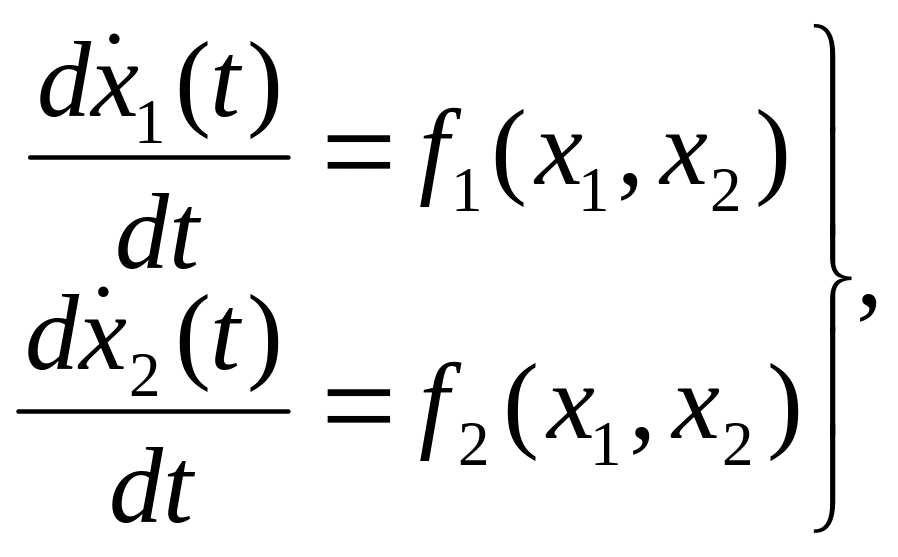(4.1)

где х_i – переменные состояния, - производные по времени этих переменных. Внешние воздействия отсутствуют, так как система рассматривается в свободном состоянии.

В общем случае порядок системы может быть .

Пространство, координатами которого являются переменные х₁,…, х_n называется фазовым. Пусть - решение системы (4.1), соответствующее определенному начальному значению , т.е. х(0)=х₀. Геометрическим местом точек х(t) для всех в фазовом пространстве является кривая, проходящая через точку х₀ и называемая траекторией системы (4.1) или фазовой траекторией. Совокупность фазовых траекторий для множества начальных условий называется фазовым портретом. Поведение траекторий в области фазового пространства, прилегающей к состояниям равновесия САУ, позволяет судить об областях устойчивости или неустойчивости системы.

Для линейных САУ фазовые траектории имеют единообразный характер во всем фазовом пространстве, поэтому фазовый портрет, построенный для области малых отклонений от состояния равновесия, дает полное представление о поведении системы при любых начальных отклонениях.

Для нелинейных САУ характер фазовых траекторий в различных областях фазового пространства может быть разным. В отличие от линейных систем, которые могут иметь лишь единственное состояние равновесия, нелинейные системы могут иметь несколько состояний равновесия. Более того, кроме траекторий, характерных для линейных САУ, в фазовых портретах нелинейных САУ могут содержаться особые фазовые траектории, присущие только нелинейным системам (предельные циклы, сепаратриссы) [2].

Построение фазовых траекторий является наглядным графическим методом исследования систем, описываемых дифференциальными уравнениями второго порядка (метод фазовой плоскости). Для систем более высокого порядка, из-за сложности многокоординатных геометрических построений, метод фазового пространства утрачивает свои достоинства.

Рассмотрим систему второго порядка (n=2). Традиционно фазовые портреты принято строить в канонических координатах, когда по оси абсцисс откладывается отклонение регулируемой координаты х, а по оси ординат ее производная по времени y=dx/dt.

Фазовые портреты линейных САУ

Линейной системе дифференциальных уравнений

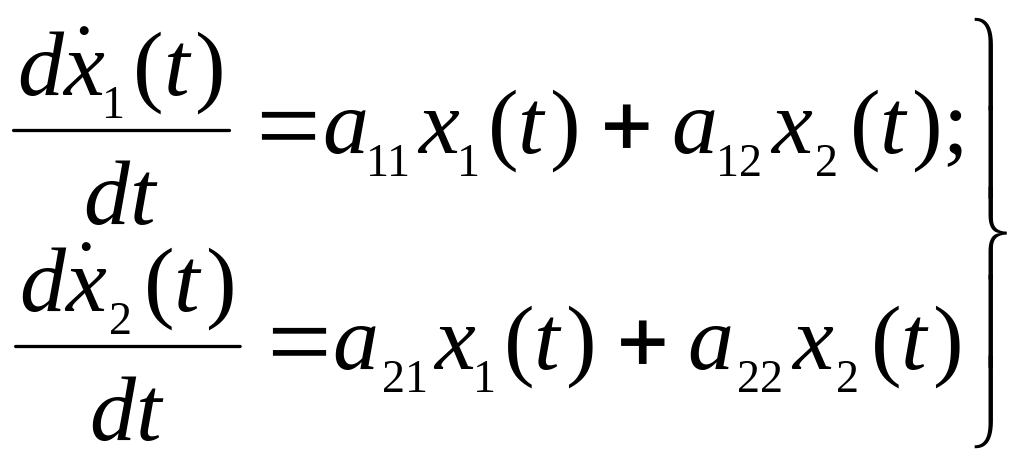(4.2)

соответствует характеристическое уравнение

(4.3)

где b=-SpA=-(a₁₁+a₂₂); c=detA=a₁₁a₂₂-a₂₁a₁₂; SpA – след матрицы А, .

Решение системы (4.2) для заданного начального состояния х₀ определяется равенством

,

где J_r – вещественная Жорданова форма, а М – вещественная невырожденная матрица, такая что М^-1АМ= J_r. В зависимости от вида корней характеристического уравнения (4.3) вещественная Жорданова форма может иметь одну из трех форм

(4.4)

где k может принимать значения 0 или 1. Первая форма соответствует случаю, когда корни характеристического уравнения λ₁, λ₂ вещественные и различные, вторая соответствует двум равным вещественным корням, третья форма соответствует двум комплексно сопряженным корням λ₁₂=α±jβ.

В зависимости от вида корней возможны следующие фазовые портреты:

1) Корни вещественные различные отрицательные λ₁=-α₁, λ₂=-α₂. При замене координат z=M^-1x, получим систему из двух дифференциальных уравнений: откуда . График апериодического переходного процесса представлен на рис. 4.1, а; фазовый портрет, называемый устойчивым узлом, представлен на рис. 4.1,б.

2) Корни вещественные различные положительные. Тогда α₁>0, α₂>0:

.

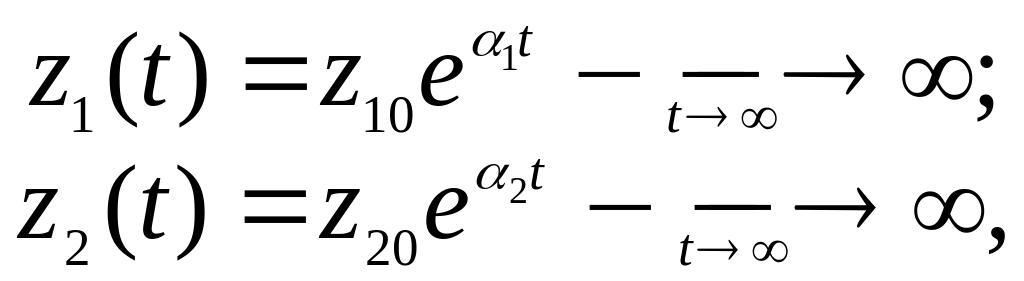т.е. графики переходных процессов представляют собой расходящийся апериодический процесс, а фазовой портрет – неустойчивый узел, который отличается от устойчивого узла противоположным направлением стрелок на траекториях.

3) Корни комплексные с отрицательными вещественными частями λ₁₂=-α±jβ. Тогда . При переходе к полярным координатам получим два раздельных дифференциальных уравнения , откуда решение при начальных условиях r₀, θ₀ имеет вид . Эти формулы определяют траекторию спирали. Переходной процесс для данного случая представлен на рис. 4.2, а, а фазовый портрет, называемый «устойчивый фокус», изображен на рис. 4.2,б.

4) Корни комплексные с положительными вещественными частями λ₁₂=α±jβ.

Тогда . Переходные процессы и фазовый портрет имеют вид, представленный на рис. 4.3; фазовый портрет является неустойчивым фокусом.

5) Корни чисто мнимые:

.

В полярных координатах решение системы имеет вид .

Фазовый портрет представляет собой набор эллипсов и называется «центром». Вид переходных процессов и фазовый портрет изображены на рис. 4.4.

6) Корни вещественные разных знаков.

.

Решение системы в этом случае

.

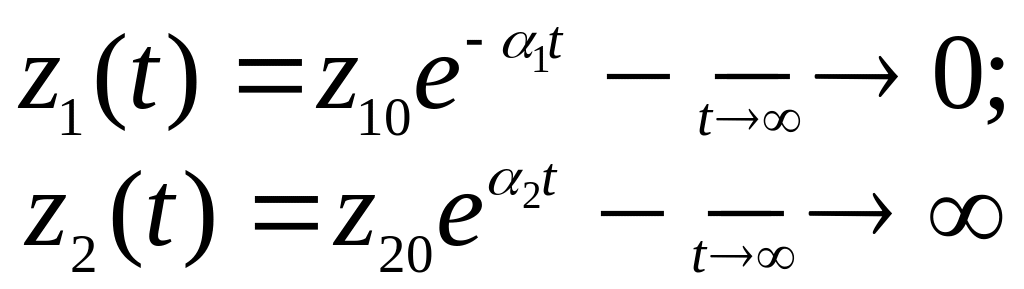Траектории системы имеют гиперболическую форму. Кроме того имеются четыре траектории, которые отличаются от гиперболических и разделяют фазовый портрет на области с различными фазовыми траекториями. Эти четыре траектории носят название сепаратрисс, причем две сепаратриссы стремятся со временем к положению равновесия. Переходной процесс и фазовый портрет для данного случая представлены на рис. 4.5. Фазовый портрет называется «седло».

Заметим, что для случая 2-х равных вещественных корней фазовый портрет имеет сходство с фазовым портретом узла, поэтому его также называют устойчивым (при λ<0) или неустойчивым узлом (λ>0). Вид фазового портрета для данного случая при Жордановой форме (4.4) для k=0 приведем на рис. 4.6.

а) б)

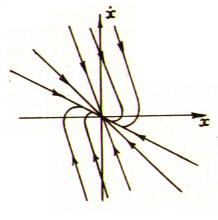
Рис. 4.1. Фазовый портрет типа «устойчивый узел»

а) б)

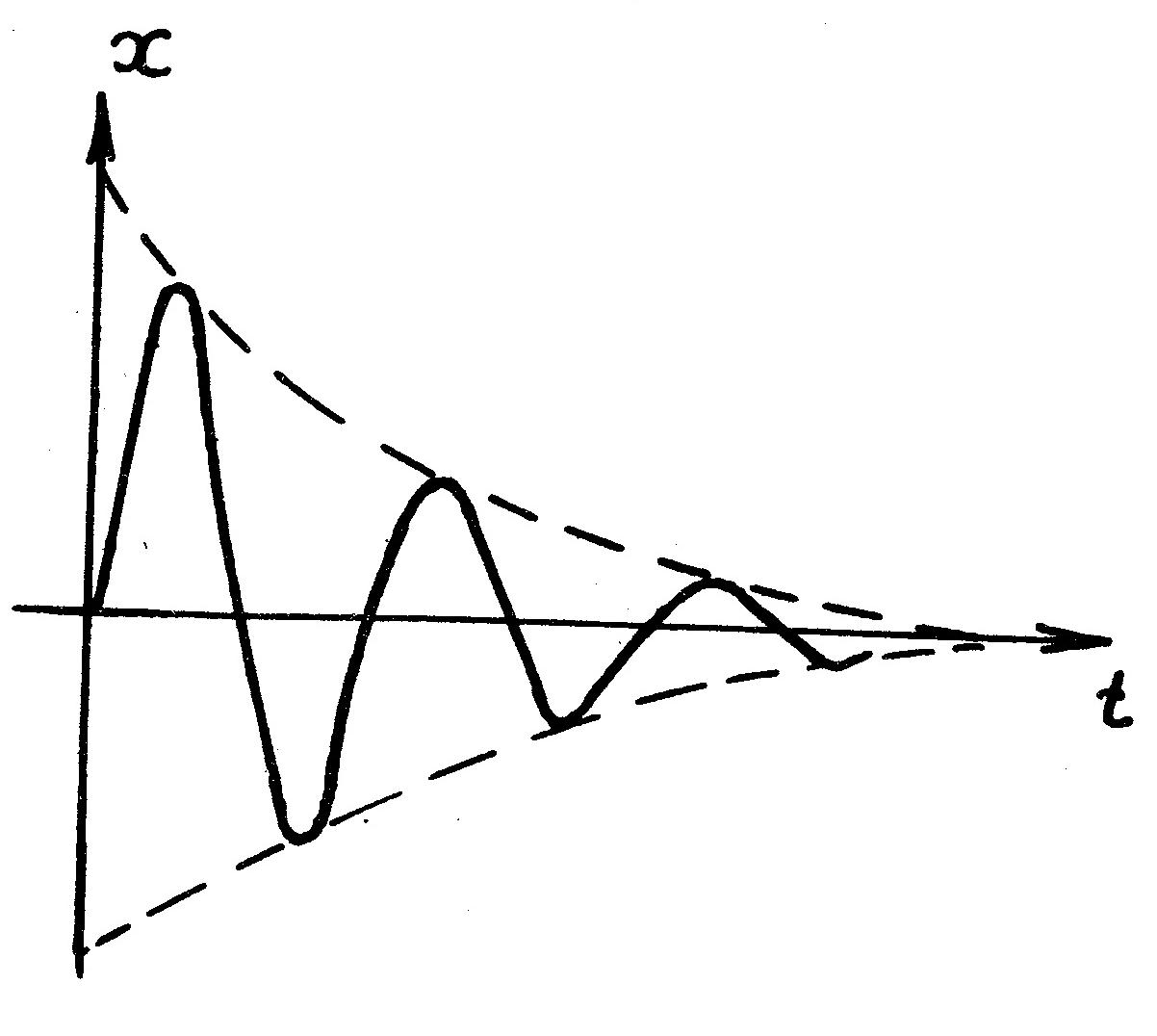
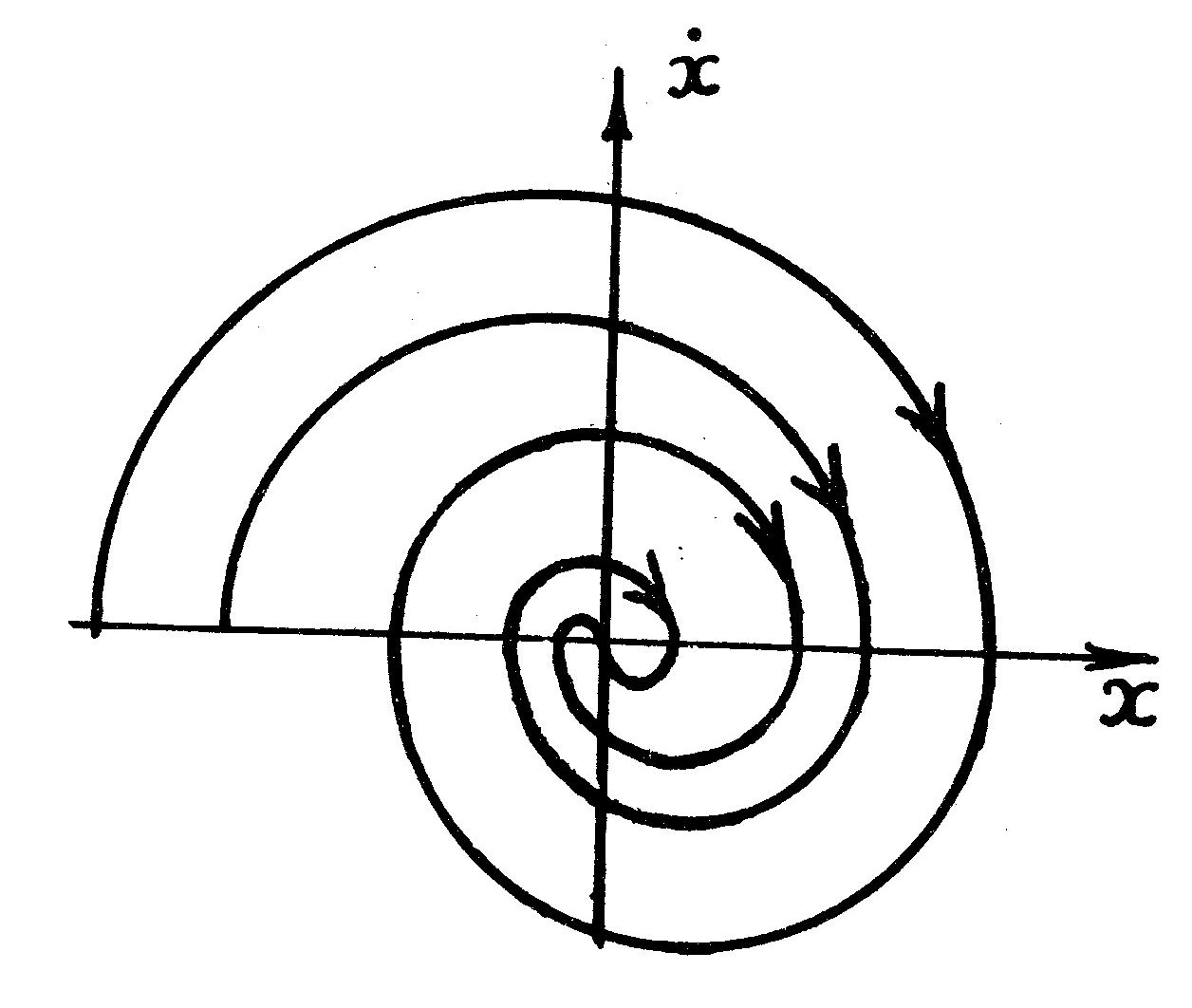
Рис. 4.2. Фазовый портрет типа «устойчивый фокус»

а) б)

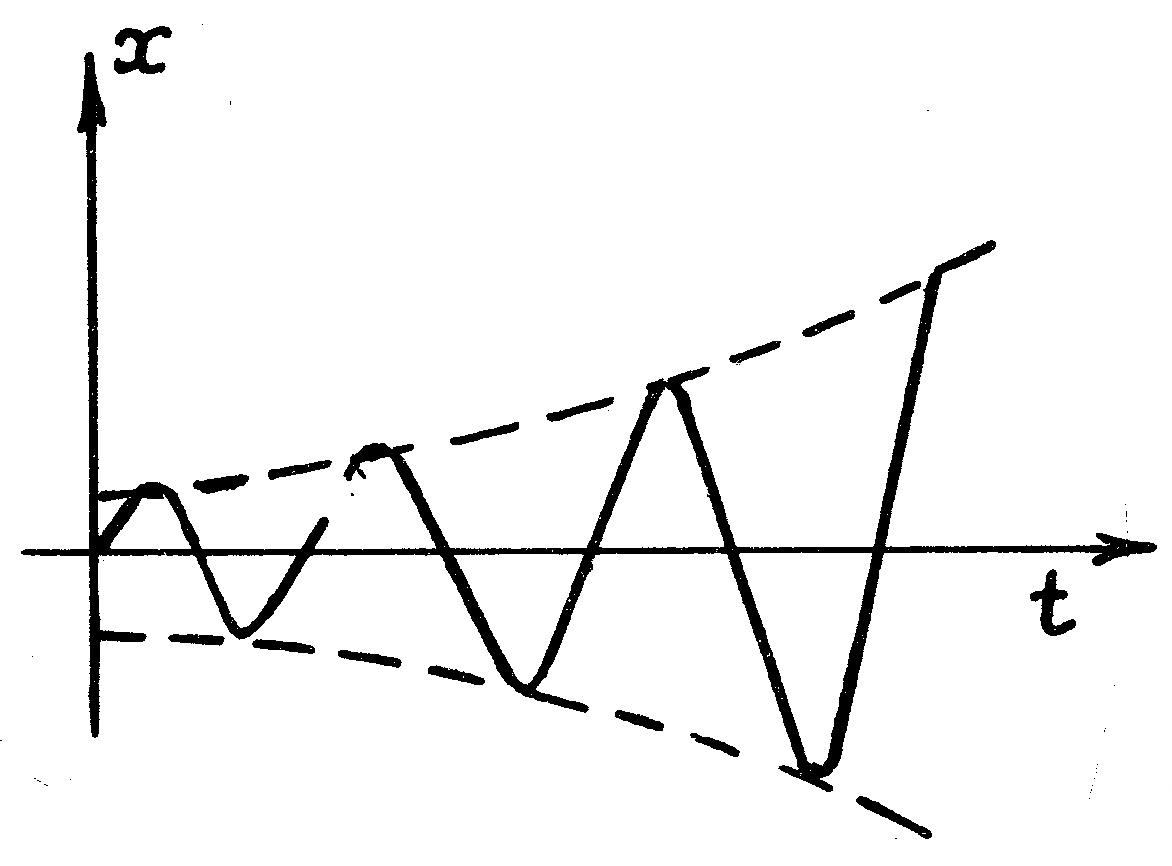
Рис. 4.3. Фазовый портрет типа «неустойчивый фокус»

а) б)

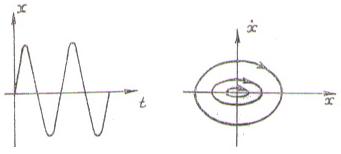
Рис. 4.4. Фазовый портрет типа «центр»

а) б)

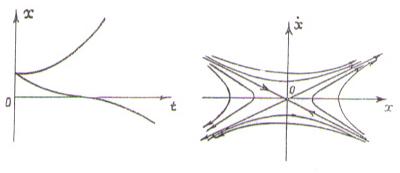
Рис. 4.5. Фазовый портрет типа «седло»

а) б)

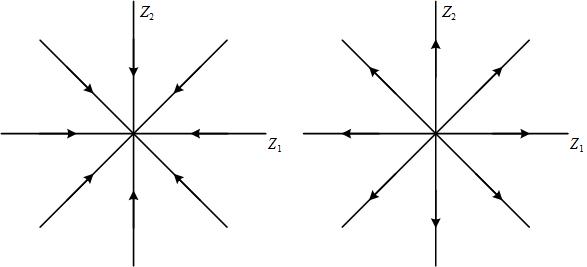
Рис. 4.6. Фазовые портреты для случая ненулевых равных вещественных корней характеристического уравнения при к=0: а) λ<0; б) λ>0.

Фазовые портреты нелинейных САУ

В нелинейных системах кроме рассматриваемых выше типов фазовых траекторий существуют еще особые фазовые траектории: предельные циклы и сепаратриссы. Предельные циклы – это замкнутые кривые на фазовой плоскости. Они соответствуют незатухающим периодическим движениям в нелинейных системах. В отличие от линейных систем амплитуда и частота этих движений не зависят от начальных условий. Периодические движения могут быть неустойчивыми и срываются при незначительном изменении амплитуды колебаний. Таким движениям соответствуют неустойчивые предельные циклы. Важно найти устойчивые предельные циклы, которые соответствуют устойчивым периодическим движениям – автоколебаниям. На рис. 4.7,а и 4.7,б изображены фазовые портреты с устойчивым и неустойчивым предельными циклами соответственно. На рис. 4.7,в изображен фазовый портрет нелинейной системы, для которого кривые, проходящие через начало координат, являются сепаратриссами.

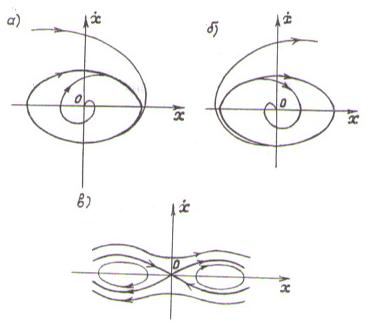
Рис. 4.7. Фазовые портреты нелинейных САУ