Министерство образования Российской Федерации

Санкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ)

Кафедра электротехники, вычислительной техники и автоматизации

ТЕОРИЯ ЛИНЕЙНЫХ И НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Методические указания к выполнению лабораторных работ

Для студентов специальности 2203.01

Составители:

Томчина О.П.

Шарякова О.Л.

Шестаков В.М.

Санкт-Петербург 2011г.

УДК 62-83

О.П. Томчина, О.Л. Шарякова, В.М. Шестаков,

Теория линейных и нелинейных систем автоматического управления: Методические указания к выполнению лабораторных работ.- СПб.: 2011.

Тематика лабораторных работ посвящена изучению динамических режимов и качества переходных процессов в линейных и нелинейных САУ, применяемых в машинных агрегатах. Работы выполняются на ЭВМ в среде пакета MATLAB-SIMULINK, что позволяет студентам освоить унифицированные системы математического моделирования и глубже изучить динамические характеристики современных САУ.

Методические указания предназначены для студентов специальности 2203.01, изучающих курс “Теория автоматического управления” (части 2 и 3).

Научный редактор докт. техн. наук, проф. В.М. Шестаков.

Рецензенты:

докт. техн. наук, проф. А.Л. Фрадков (Институт проблем машиноведения РАН); канд. техн. наук, доц. А.Е. Епишкин (ПИМаш)

Содержание

Работа №1. Исследование настройки типового контура на оптимум по модулю………………………………………………………………………………4

Работа №2. Исследование настройки типового контура на симметричный оптимум……………………………………………………………………………..9

Работа №3. Исследование настройки типового контура на скорректированный оптимум…………………………………………………………………………….13

Работа №4. Исследование динамики линейных и нелинейных САУ с помощью метода фазовой плоскости……………………………………….………………..18

Литература………………………………………………………………….………32

Приложение………………………………………………………………..………..33

Лабораторная работа №1

Исследование настройки типового контура на оптимум по модулю

Цель работы: Исследование качества переходных процессов по управлению и возмущению в замкнутом контуре, настроенном на оптимум по модулю.

1. Основные сведения

В современных системах автоматического управления широкое применение нашла структура подчиненного регулирования. Система подчиненного регулирования, характеризуется последовательным включением корректирующих устройств и обладает следующими особенностями [1]:

1) количество регуляторов равно количеству локальных объектов управления;

2) все регуляторы включены в систему последовательно таким образом, что каждый внутренний регулятор подчинен смежному с ним внешнему;

3) локальный объект управления представляет собой типовое звено первого или второго порядка и содержит, как правило, одну большую постоянную времени контура;

4) регулятор является типовым и имеет типовые настройки.

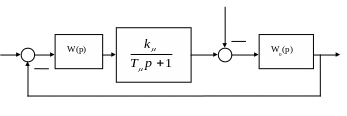
На рис. 1.1 приведена динамическая структурная схема типового контура.

z

х y

Рис. 1.1. Типовой контур системы подчиненного регулирования

x – сигнал задания, z –возмущающее воздействие, y – регулируемая переменная, W(p) – передаточная функция регулятора, W₀(р) – передаточная функция локального объекта управления, k_µ - коэффициент передачи звена с малой постоянной времени Т_µ.

Пусть локальный объект управления – апериодическое звено первого порядка с передаточной функцией

W₀(p) = k₀/(T₀р+1),

где T₀ – большая постоянная времени контура (T₀>> Тµ), k₀- коэффициент передачи объекта. Применяя пропорционально-интегральный (ПИ) регулятор с передаточной функций , найдем параметры регулятора

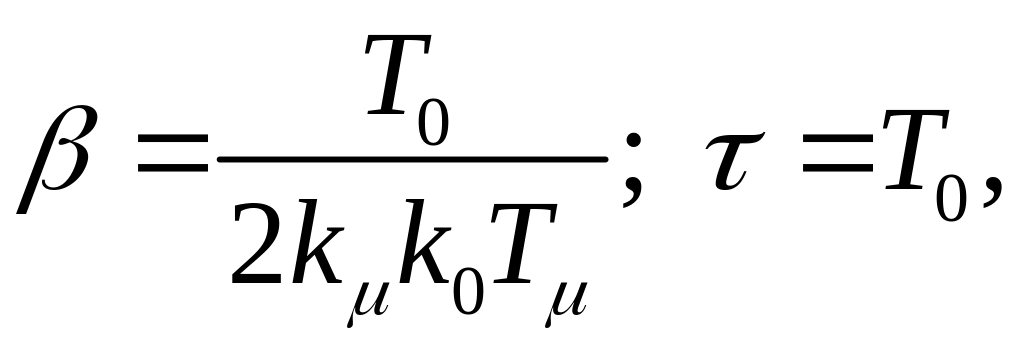(1.1)

где β — динамический коэффициент усиления, τ — постоянная времени настройки регулятора.

Реализация настройки на ОМ возможна и при других передаточных функциях объекта.

Если W₀(p)=k₀/(T₀p), то должен быть использован пропорциональный (П) регулятор W_p(p)=β (см. формулу 1.1).

Если объект содержит две «большие» постоянные времени Т₀₁ и Т₀₂

,

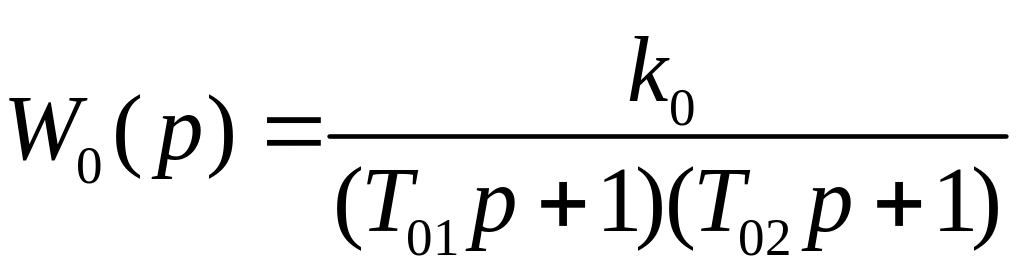то аналогичный результат может быть получен при применении пропорционально-интегрально-дифференциального (ПИД) регулятора

(1.2)

с параметрами 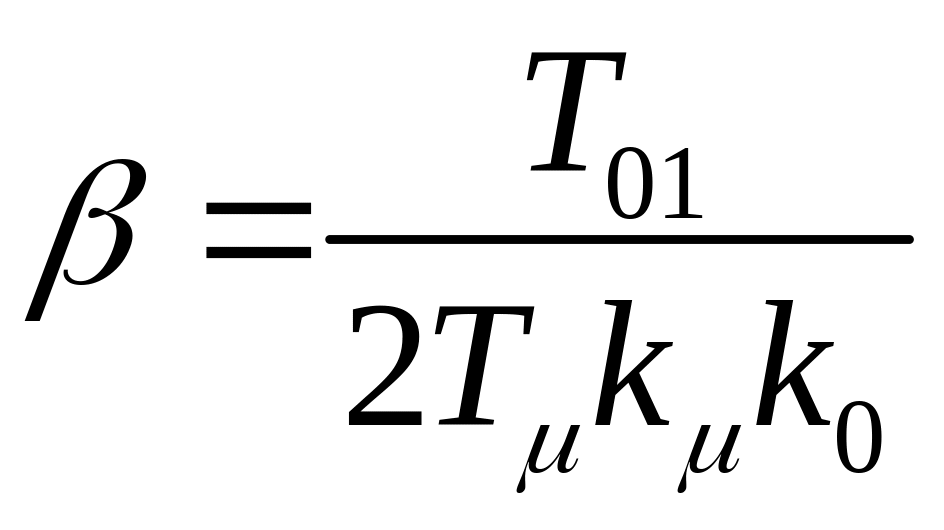, τ₁=T₀₁ и τ₂=T₀₂ при условии T₀₁>T₀₂.

Передаточная функция замкнутого оптимизированного контура по управляющему воздействию будет

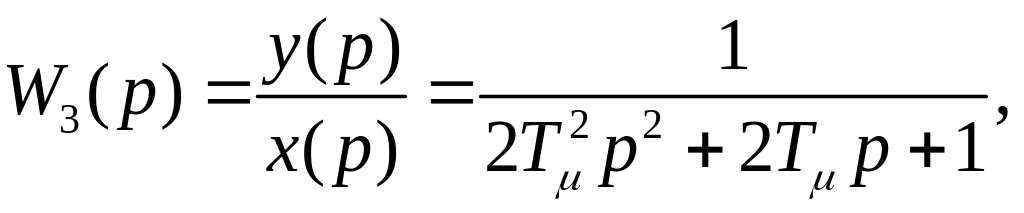при представлении знаменателя в виде коэффициент демпфирования .

При ступенчатом управляющем воздействии выходная координата в первый раз достигает установившегося значения через время 4,7Т_μ при перерегулировании 4,3 % (рис. 1.2). Длительность переходного процесса не зависит от постоянной времени объекта Т₀ и определяется малой постоянной времени Т_μ. Такой способ настройки контура называется настройкой на оптимум по модулю (ОМ). Наиболее простое объяснение этого термина состоит в том, что при данной настройке стремятся в наиболее широкой полосе частот сделать модуль вещественной частотной характеристики замкнутого контура близким к единице.

На рис. 1.3 представлены логарифмические частотные характеристики разомкнутой САУ. Запас устойчивости по фазе составляет Δφ_р=63⁰

При настройке контура на ОМ длительность переходного процесса по возмущению определяется соотношением постоянных времени Т₀ и Т_μ. Чем больше Т₀, тем ниже быстродействие системы по возмущению (см. рис 1.4).

Таким образом, настройка на ОМ – это настройка на оптимальное быстродействие по управляющему воздействию.

В ряде случаев может быть применена настройка на компромиссный оптимум (КО), обеспечивающая большее быстродействие, чем ОМ. При настройке на КО параметры ПИ-регулятора: 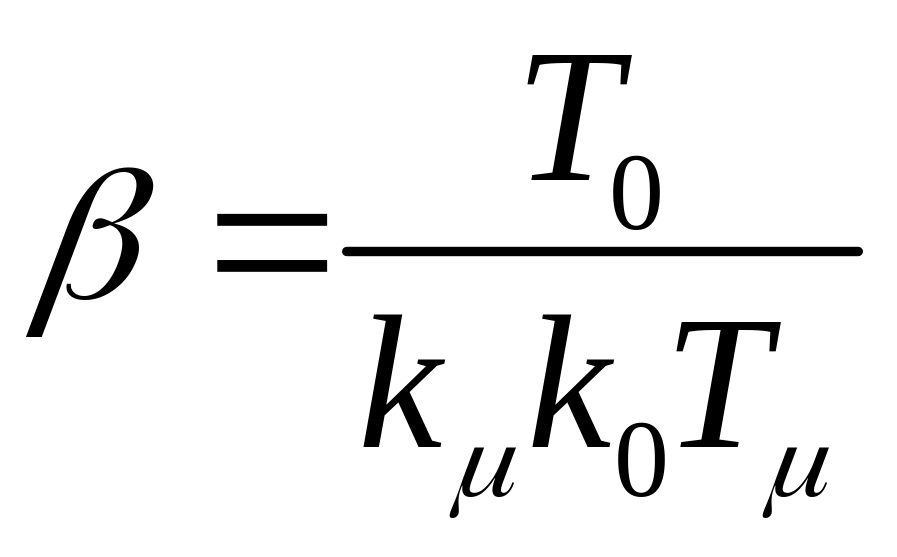, τ=T₀. При этом уменьшается время переходного процесса, но увеличивается перерегулирование и составляет 16% (см. рис. 1.5).

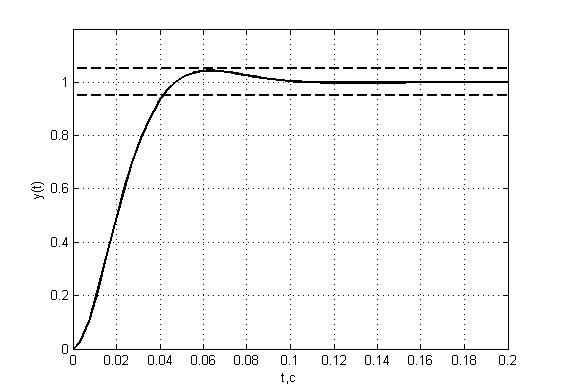
Рис. 1.2. Переходная функция контура при настройке на ОМ

.

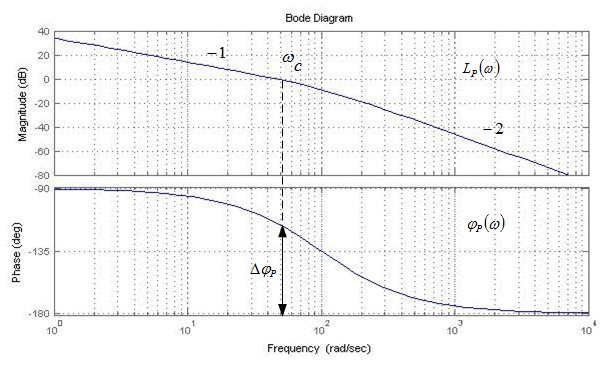
Рис. 1.3. ЛАХ и ЛФХ разомкнутой САУ

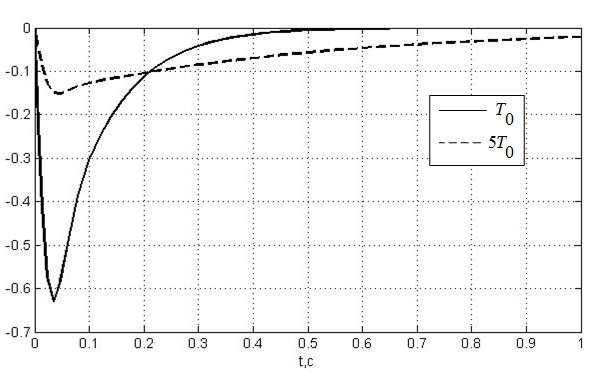
Рис. 1.4. Переходные функции контура по возмущению

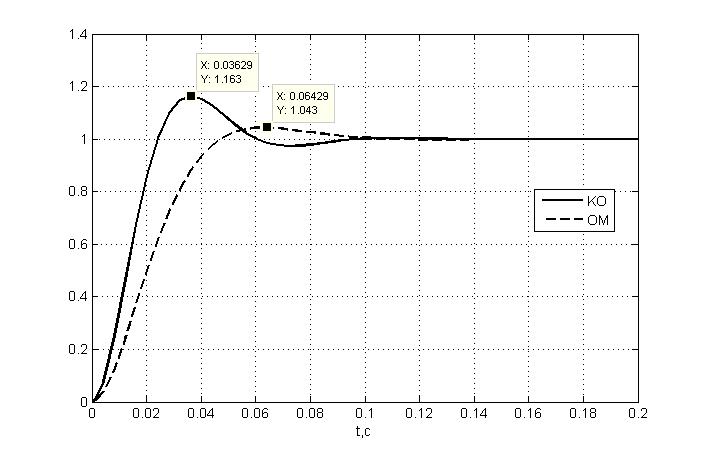
Рис. 1.5. Переходные функции контура при настройках на КО и ОМ