Критичні значення Lкр для критерію Тітьєна – Мура l(k) і з кількістю викидів k та об'ємом вибірки n
α = 0,10 |
||||||||||
N |
k |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
3 |
0,011 |
|
|
|
|
|
|
|
|
|
4 |
098 |
0,003 |
|
|
|
|
|
|
|
|
5 |
200 |
038 |
|
|
|
|
|
|
|
|
6 |
280 |
091 |
0,020 |
|
|
|
|
|
|
|
7 |
348 |
148 |
056 |
|
|
|
|
|
|
|
8 |
404 |
200 |
095 |
0,038 |
|
|
|
|
|
|
9 |
448 |
248 |
134 |
068 |
|
|
|
|
|
|
10 |
490 |
287 |
170 |
098 |
0,051 |
|
|
|
|
|
11 |
526 |
326 |
208 |
128 |
074 |
|
|
|
|
|
12 |
555 |
361 |
240 |
159 |
103 |
0,062 |
|
|
|
|
13 |
578 |
388 |
270 |
186 |
126 |
082 |
|
|
|
|
14 |
600 |
416 |
298 |
212 |
150 |
104 |
0,068 |
|
|
|
15 |
611 |
436 |
322 |
236 |
172 |
124 |
086 |
|
|
|
16 |
631 |
458 |
342 |
260 |
194 |
144 |
104 |
0,073 |
|
|
17 |
648 |
478 |
354 |
282 |
216 |
165 |
125 |
093 |
|
|
18 |
661 |
496 |
384 |
302 |
236 |
184 |
142 |
108 |
0,080 |
|
19 |
676 |
510 |
398 |
316 |
251 |
199 |
158 |
124 |
094 |
|
20 |
688 |
530 |
420 |
339 |
273 |
220 |
176 |
140 |
110 |
0,085 |
25 |
732 |
588 |
489 |
412 |
350 |
296 |
251 |
213 |
180 |
152 |
30 |
766 |
637 |
523 |
472 |
411 |
359 |
316 |
276 |
240 |
210 |
35 |
792 |
673 |
586 |
516 |
458 |
410 |
365 |
328 |
294 |
262 |
40 |
812 |
702 |
622 |
554 |
499 |
451 |
406 |
372 |
338 |
307 |
45 |
826 |
724 |
648 |
586 |
533 |
488 |
447 |
410 |
378 |
348 |
50 |
840 |
744 |
673 |
614 |
562 |
518 |
477 |
442 |
410 |
380 |
Продовження табл. 4
α = 0,05 |
||||||||||
N |
k |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
3 |
0,003 |
|
|
|
|
|
|
|
|
|
4 |
051 |
0,001 |
|
|
|
|
|
|
|
|
5 |
125 |
018 |
|
|
|
|
|
|
|
|
6 |
203 |
055 |
0,010 |
|
|
|
|
|
|
|
7 |
273 |
106 |
032 |
|
|
|
|
|
|
|
8 |
326 |
146 |
064 |
0,022 |
|
|
|
|
|
|
9 |
372 |
194 |
099 |
045 |
|
|
|
|
|
|
10 |
418 |
233 |
129 |
070 |
0,034 |
|
|
|
|
|
11 |
454 |
270 |
162 |
098 |
054 |
|
|
|
|
|
12 |
489 |
305 |
196 |
125 |
076 |
0,042 |
|
|
|
|
13 |
617 |
337 |
224 |
150 |
098 |
060 |
|
|
|
|
14 |
540 |
363 |
250 |
174 |
122 |
079 |
0,050 |
|
|
|
15 |
556 |
387 |
276 |
197 |
140 |
097 |
066 |
|
|
|
16 |
575 |
410 |
300 |
219 |
159 |
115 |
082 |
0,055 |
|
|
17 |
594 |
427 |
322 |
240 |
181 |
136 |
100 |
072 |
|
|
18 |
608 |
447 |
337 |
259 |
200 |
154 |
116 |
086 |
0,062 |
|
19 |
624 |
462 |
354 |
277 |
209 |
168 |
130 |
099 |
074 |
|
20 |
639 |
484 |
377 |
299 |
238 |
188 |
150 |
115 |
088 |
0,066 |
25 |
696 |
550 |
450 |
374 |
312 |
262 |
222 |
184 |
154 |
126 |
30 |
730 |
599 |
506 |
434 |
376 |
327 |
283 |
245 |
212 |
183 |
35 |
762 |
642 |
554 |
482 |
424 |
376 |
334 |
297 |
264 |
235 |
40 |
784 |
672 |
588 |
523 |
468 |
421 |
378 |
342 |
310 |
280 |
45 |
802 |
696 |
618 |
556 |
502 |
456 |
417 |
382 |
350 |
320 |
50 |
820 |
722 |
646 |
588 |
535 |
490 |
450 |
414 |
383 |
356 |
α = 0,01 |
||||||||||
3 |
0,000 |
|
|
|
|
|
|
|
|
|
4 |
011 |
0,000 |
|
|
|
|
|
|
|
|
5 |
045 |
004 |
|
|
|
|
|
|
|
|
6 |
091 |
021 |
0,002 |
|
|
|
|
|
|
|
7 |
148 |
047 |
010 |
|
|
|
|
|
|
|
8 |
202 |
076 |
028 |
0,008 |
|
|
|
|
|
|
9 |
235 |
112 |
048 |
018 |
|
|
|
|
|
|
10 |
280 |
142 |
070 |
032 |
0,012 |
|
|
|
|
|
11 |
327 |
178 |
098 |
052 |
026 |
|
|
|
|
|
12 |
371 |
208 |
120 |
070 |
038 |
0,019 |
|
|
|
|
13 |
400 |
233 |
147 |
094 |
056 |
033 |
|
|
|
|
14 |
424 |
267 |
172 |
113 |
072 |
046 |
0,027 |
|
|
|
15 |
450 |
294 |
194 |
132 |
090 |
057 |
037 |
|
|
|
16 |
473 |
311 |
219 |
151 |
108 |
072 |
049 |
0,030 |
|
|
17 |
480 |
338 |
237 |
171 |
126 |
091 |
064 |
044 |
|
|
18 |
502 |
358 |
260 |
192 |
140 |
104 |
076 |
053 |
0,036 |
|
19 |
508 |
366 |
272 |
201 |
154 |
118 |
088 |
064 |
046 |
|
20 |
533 |
387 |
300 |
231 |
175 |
136 |
104 |
078 |
058 |
0,042 |
25 |
603 |
468 |
377 |
308 |
246 |
204 |
168 |
144 |
112 |
092 |
30 |
650 |
526 |
434 |
369 |
312 |
268 |
229 |
196 |
166 |
142 |
35 |
690 |
574 |
484 |
418 |
364 |
321 |
282 |
250 |
220 |
194 |
40 |
722 |
608 |
522 |
460 |
408 |
364 |
324 |
292 |
262 |
234 |
45 |
745 |
636 |
558 |
498 |
444 |
399 |
361 |
328 |
296 |
270 |
50 |
768 |
668 |
592 |
531 |
483 |
438 |
400 |
368 |
336 |
308 |
2. Перевірка гіпотези нормальності розподілу
Для вибірок невеликих об'ємів застосовуються прості критерії, що використовуються як «приблизні» при великому об'ємі вибіркових даних. Вони засновані на використанні коефіцієнта варіації, середнього абсолютного відхилення (САВ), розмаху варіювання, показниках асиметрії та ексцесу. Висновок про підтвердження гіпотези нормальності на основі даних малої вибірки можна зробити лише при здобутті позитивних результатах перевірки декількома критеріями цієї групи.
2.1. Перевірка по коефіцієнту варіації
Перевірку гіпотези нормальності починають з обчислення коефіцієнта варіації (V):
(8)
Якщо значення коефіцієнта варіації перевищує 33%, то гіпотеза про нормальність розподілу даних вибірки не підтверджується. Подальшу перевірку при цьому не проводять, оскільки такі розподіли повинні перетворюватися з метою зменшення коефіцієнта варіації. При зворотному співвідношенні, перевірку продовжують по критеріях, що залишилися.
2.2. Критерій середнього абсолютного відхилення (САВ)
Для не великих вибірок (N ≤ 120) використовують показник САВ, що визначається за такою формулою:
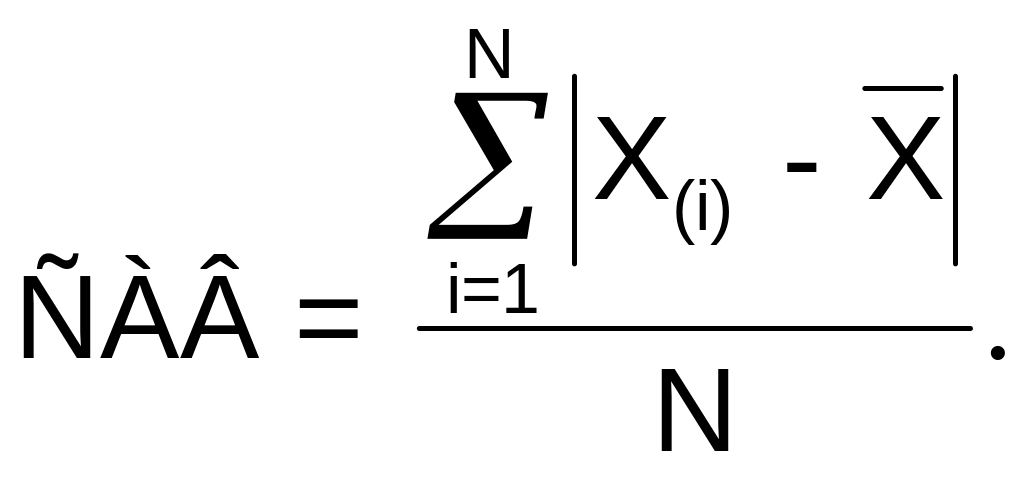(9)
Відомо,
що для теоретичного нормального розподілу
відношення САВ / σ (σ2
– дисперсія теоретичного розподілу)
дорівнює
.
Для вибірки, що має приблизно нормальний
закон розподілу, повинне виконуватися
таке співвідношення:
(10)
2.3. Перевірка за розмахом варіювання (R / S критерій)
Дана перевірка може бути проведена для широкого класу вибірок з об'ємом 3 ≤ N ≤ 1000.
Розмах варіювання R розраховують як різницю між найбільшим і найменшим елементами у вибірці, або в термінах побудованого за вибіркою x1, x2, …, xN варіаційного ряду x(1) ≤ x2 ≤ … ≤ x(N): R = x(N) – x(1).
Далі розраховують критеріальне відношення R / SN, яке зіставляють з критичними значеннями верхнього і нижнього кордонів для різних рівнів значущості. Якщо розраховане відношення лежить в межах кордонів, гіпотезу про нормальність розподілу приймають, якщо ж воно менше нижнього кордону або більше верхньою – гіпотезу відкидають.
Для упевненого ухвалення рішення про нормальність даних вибірки важливо, аби умова знаходження усередині кордонів виконувалася на жорсткому 10 %-ому рівні значущості (p = 0,1). Проте, якщо гіпотеза нормальності підтверджується всіма іншими критеріями, можна обмежитися виконанням умови й на 5 %-ому рівні значущості (p = 0,05).
Критичні значення R / S критерію подано у табл. 5.
Таблиця 5