
Pridumay_sam_42859
.docx
Содержание
1.1 Подвижность механизма 1
1.2 Структурные группы и класс механизма 2
1.2 Метрический синтез и построение планов рычажного механизма 3
1.3.Динамический синтез рычажного механизма 4
1.3.1 Построение планов скоростей, 4
1.3.11 Построение планов ускорений, определение 7
В качестве используемого механизма, служащего для привода пресса в данном проекте используется плоский шестизвенный механизм. Он является кривошипно-карамысловым, преобразующим вращательное движение кривошипа в возвратно-поступательное движение ползуна 5 (рис. 1.1).

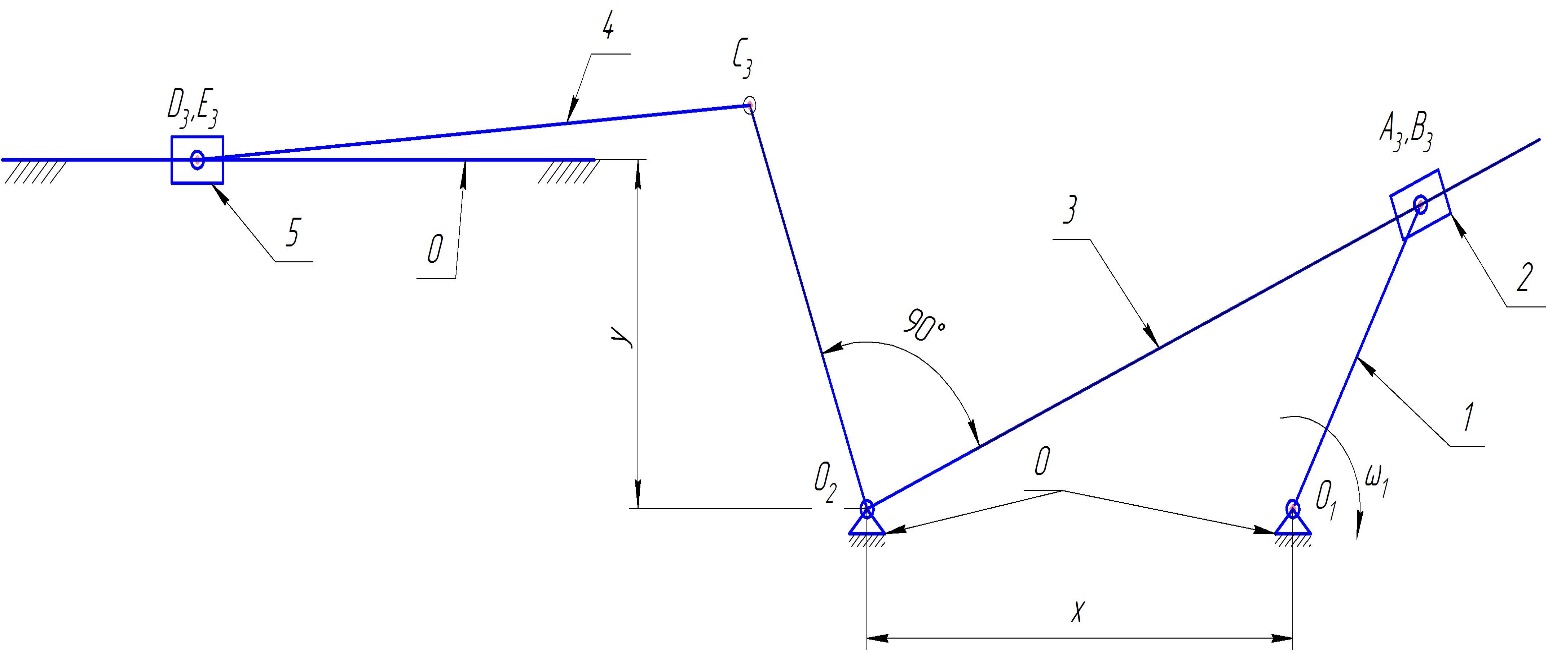
Рисунок 1.1 – Структурная схема рычажного механизма
Выполним структурный анализ рычажного механизма, определим его подвижность и класс.
1.1 Подвижность механизма
Проанализируем звенья, а также вид совершаемого ими движения, кинематические пары, соединяющие эти звенья (рис 1.1).
Данный механизм является плоским кривошипно-карамысловым, воспользуемся формулой Чебышева для вычисления подвижности плоского механизма:
 (1.1)
(1.1)
Таблица 1.2 – Кинематические пары механизма
Обозначение пары |
О1 |
А |
В |
О2 |
С |
Д1 |
Д2 |
Номера звеньев, образующих пары |
0-1 |
1-2 |
2-3 |
0-3 |
3-4 |
4-5 |
0-5 |
Класс пары |
V |
V |
V |
V |
V |
V |
V |
Вид пары |
ВКП |
ВКП |
ВКП |
ВКП |
ВКП |
ВКП |
ВКП |
Где:
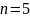 – число подвижных
звеньев механизма;
– число подвижных
звеньев механизма;
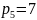 – число кинематических
пар V
класса;
– число кинематических
пар V
класса;
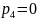 –
число кинематических
пар IV
класса.
–
число кинематических
пар IV
класса.
Следовательно, подвижность механизма, изображенного на рис.1.1, определим из формулы (1.2):
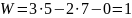
следовательно данный механизм имеет одно входное звено – кривошип 1.
1.2 Структурные группы и класс механизма
Схема любого плоского механизма может быть создана последовательным присоединением к ведущему звену и стойке кинематических цепей, которые не меняют подвижность механизма. Разобьем данный рычажный механизм на структурные группы – простейшие кинематические цепи с нулевой подвижностью относительно тех звеньев, с которыми входят в кинематические пары V класса свободные элементы их звеньев, и не распадающихся на более простые кинематические цепи также с нулевой подвижностью. Отсоединение структурных групп начинаем со структурной группы, наиболее удаленной от входного звена. На рис.1.2 представлен первичный механизм и структурные группы механизма.

II (4,5)2,2

II (2,3)2,1
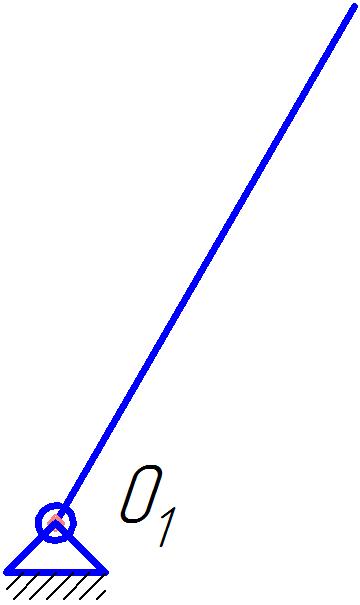 I(1,0)
I(1,0)
Рисунок 1.2 – Структурные группы рычажного механизма
Запишем структурную формулу строения механизма:
I(0,1)→II(2,3)2,1→II(4,5)2,2
1.2 Метрический синтез и построение планов рычажного механизма
Обозначим т. О1 (стойка);
Построим при помощи масштабного коэфициэнта звено 1;
Построим 12 положений звена 1;
От O1 отложим величину, x и обозначим точку O2;
Строим звено 3, и определяем крайние положения точки С;
От т О2 по вертикали откладываем значение, y и на этом расстоянии проводим горизонтальную линию-ось О3;
Из очки С откладываем звено 4 до пересечения с линией оси, определяем максимальное перемешение ползуна 5;
1.3.Динамический синтез рычажного механизма
Цель динамического
синтеза рычажного механизма – определение
параметров махового колеса, необходимым
для обеспечения заданного коэффициента
неравномерности движения механизма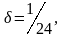 который обеспечивается также величиной
приведенного момента инерции добавочных
масс.
который обеспечивается также величиной
приведенного момента инерции добавочных
масс.
Входные параметры:
- кинематические размеры звеньев ;
- средняя чистота вращения кривошипа nкр=82 мин-1;
1.3.1
Построение планов скоростей,

Планы скоростей – графическое построение в некотором масштабе векторов абсолютных и относительных скоростей звеньев механизма.
Вычисляем угловую скорость кривошипа 1:

где nкр=82 об/мин – частота вращения кривошипа.
Скорость конца кривошипа:
 .
.
Для построения планов скоростей рычажного механизма решим графически системы векторных уравнений, связывающих неизвестные скорости внутренних точек структурных групп механизма с известными скоростями крайних.
Указанные векторные уравнения для структурных групп рассматриваемого механизма имеют вид:
для точки В:
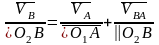 (1.5)
(1.5)
Для точки D:
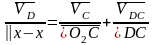 (1.6)
(1.6)
Выбираем масштабный коэффициент планов скоростей
µV=0,01407(м/с∙мм),
тогда скорость точки А изображаем отрезком
 .
.
Пользуясь векторными уравнениями (1.5)-(1.6), строим планы скоростей для всех рассматриваемых положений рычажного механизма, считая звенья однородными стержнями. Воспользуемся теоремой подобия для определения скоростей центров масс звеньев. Рассчитаем скорости характерных точек и угловые скорости звеньев.
Используя полученные планы для всех рассматриваемых положений механизма определим значения линейных скоростей точек В, С, А и угловые скорости звеньев 2, 3, 4, а также линейные скорости центров масс звеньев механизма:
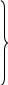
 ;
;


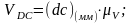

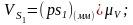 (1.7)
(1.7)
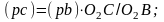
;
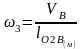 ;
;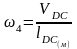 ;
;
Для примера, используя формулы 1.7, рассчитаем скорости точек звеньев механизма в положении 3
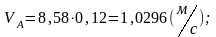
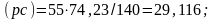


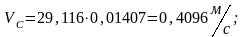
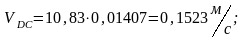
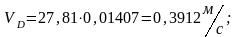
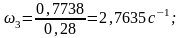
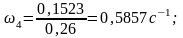
ω5=0, т.к. звено 5 совершает поступательное движение.
Аналогично рассчитываем скорости для остальных положений механизма.
Полученные результаты сводим в таблицу 1.3.
Таблица 1.3 – Кинематические параметры механизма
Скоросстя |
Положения |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Va |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
|
Vb |
0,1129821 |
0,506661 |
0,77385 |
0,9321375 |
0,9849 |
0,932138 |
0,77385 |
0,506661 |
0,112982 |
0,462622 |
0,9849 |
0,462622 |
|
Vba |
0,9784278 |
0,844481 |
0,609231 |
0,317982 |
1,0296 |
0,317982 |
0,609231 |
0,844481 |
1,0296 |
1,0296 |
1,0296 |
1,0296 |
|
Vc |
0,0961936 |
0,32242 |
0,410141 |
0,4466555 |
0,456747 |
0,446655 |
0,410141 |
0,32242 |
0,096194 |
0,606476 |
1,82699 |
0,606476 |
|
Vcd |
0,0572649 |
0,165885 |
0,152378 |
0,0869526 |
0 |
0,086953 |
0,15266 |
0,165885 |
0,057265 |
0,321359 |
0 |
0,321359 |
|
Vd |
0,0960981 |
0,281541 |
0,391287 |
0,4470039 |
0,456712 |
0,429276 |
0,3699 |
0,27127 |
0,077104 |
0,506098 |
1,77071 |
0,522701 |
|
1.3.11
Построение планов ускорений, определение
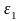
Составление векторных уравнений для построения планов ускорений основана на использовании теоремы об ускорениях точек плоских фигур.
Условно обозначим ω1=const.
Определим ускорение конца кривошипа, т.е. точки А:
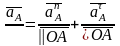 (1.8)
(1.8)
где аАτ – тангенциальное ускорение точки А, которое определяется по формуле:
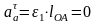 т.к.
т.к.

aAn – нормальное ускорение точки А, которое определяется по формуле:

Следовательно,
ускорение точки А равно
 Векторные уравнения для построения
планов ускорений рассматриваемого
механизма имеют вид:
Векторные уравнения для построения
планов ускорений рассматриваемого
механизма имеют вид:
Ускорение точки В:
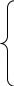
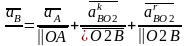 (1.9)
(1.9)

где, – нормальное ускорение, которое
определяется по формуле:
– нормальное ускорение, которое
определяется по формуле:
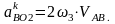 (1.10)
(1.10)
 -
релятивное
ускорение, направленное вдоль кулисы
-
релятивное
ускорение, направленное вдоль кулисы
Длина вектора на плане скоростей:
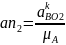 ;
(1.11)
;
(1.11)
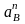 - нормальное
ускорение, которое определяется по
формуле:
- нормальное
ускорение, которое определяется по
формуле:
![]()
 (1.12)
(1.12)
Длина вектора на плане скоростей:
 (1.13)
(1.13)
Ускорение точки D:
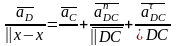 (1.14)
(1.14)
где
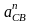 - нормальное ускорение, которое
определяется по формуле:
- нормальное ускорение, которое
определяется по формуле:
 (1.15)
(1.15)
Длина вектора на плане скоростей:
 (1.16)
(1.16)
Из плана ускорений определим:

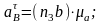
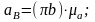
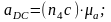
 (1.17)
(1.17)
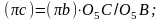
Угловые ускорения рычажных звеньев определим по формулам:
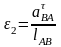 ;
;
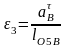 ;
;
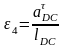 .
(1.19)
.
(1.19)
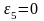 ,
т.к. звено совершает поступательное
движение.
,
т.к. звено совершает поступательное
движение.
По приведенным векторным уравнениям (1.8), (1.9) и (1.14) построим планы ускорений механизма положения – 3
Выбираем масштабный коэффициент:
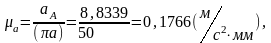
где (πа)=80мм – длина вектора ускорения конца кривошипа.
Используя формулы (1.10)-(1.13) и (1.15)-(1.16) определим нормальные ускорения:

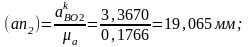
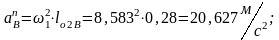


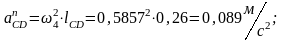

Из плана ускорения по формулам (1.17)-(1.19) определим;
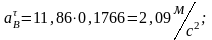
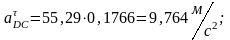
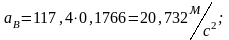
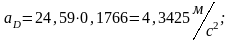
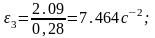
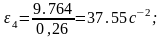
, т.к. звено 5 совершает поступательное движение.
