Сравнительная таблица показателиадекватности

Порядки (структуры) моделей регуляторов и каналов объекта		Расчётные значения критерия Фишера	Табличное значение критерия Фишера (p=0.01, f1=120, f2=120)
	1 паряд.	172,848	1,53
	3 паряд.	4,056.103

Вывод:осуществил параметрическую идентификацию дискретных динамических моделей основного канала, используя метод наименьших квадратов, составил систему уравнений и решил ее относительно определяемых коэффициентов. Качество аппроксимации оценил по критерию Фишера, сравнивая расчётное значение критерия Фишера Fобъекта 1-го и 3-го порядка, заметим что оба превышают табличное значениеF_табл. Но объект 3-го порядка более превышает F_табл и из этого можно сделать вывод о том, что модель объекта 3-го порядка достаточно точно описывает имитационную зависимость.

1.2. Параметрическая идентификация дискретных динамических моделей канала возмущения.

1. Задаем системной переменной значение 1.

2. Исходные данные:

В качестве исходные данные было использованный значения подобранный из исходного графика (первый график) рис.3 и с их помощью построили график и осуществили дальнейшие вычисления.

- Число точки подобранный из исходного графика.

- Управляющий воздействие.

- пути к файлу имеющий подобранныеточки.

1.2.1. Идентификация уравнения 1-го порядка

- Общий число итераций

- число такта квантования

- целое число тактов запаздывания

- время чистого запаздывания

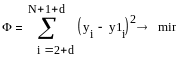
3. Взяв частные производные по каждому параметру и прировняв их к нулю получим систему уравнений относительно неизвестных коэффициентов.

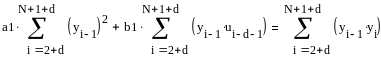
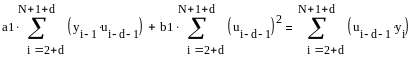
3. Решим полученную систему методом Крамера, запишем матрицу системы.

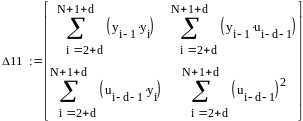
3. Найдем коэффициенты системы уравнений.

6. Заполним массив у в соответствии с полученным разностным уравнением:

Построим график:

6. Проверка адекватности при отсутствии параллельных опытов по критерию Фишер.

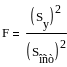
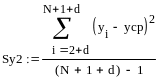
ч исло связей наложенных на модель:

6. Рассчитаем критерий Фишера.