Точку пересечения параболы на отрезке с осью абсцисс находим из системы
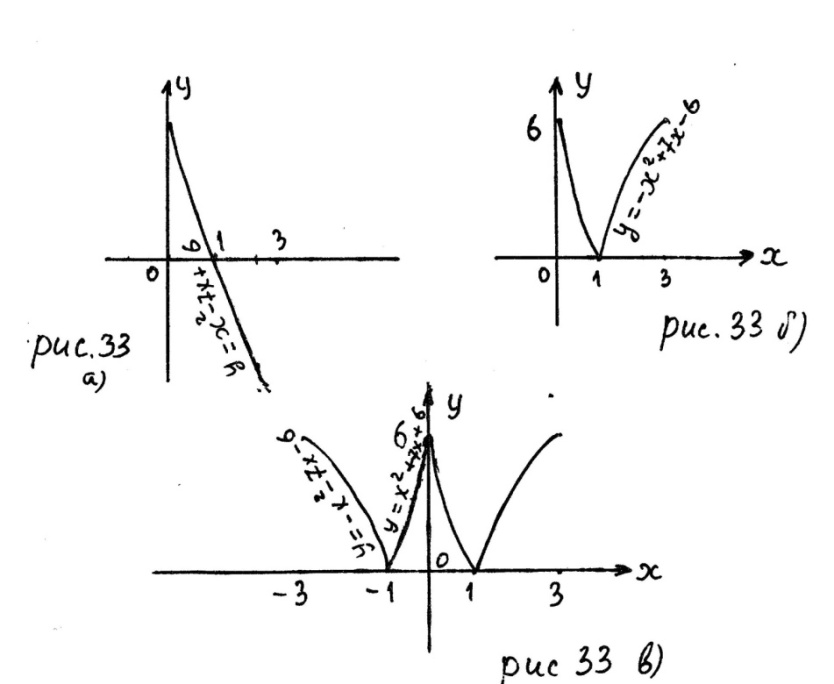
Строим график параболы на отрезке (рис. 33 а)).
2. Строим график функции на отрезке (рис. 33 б)).
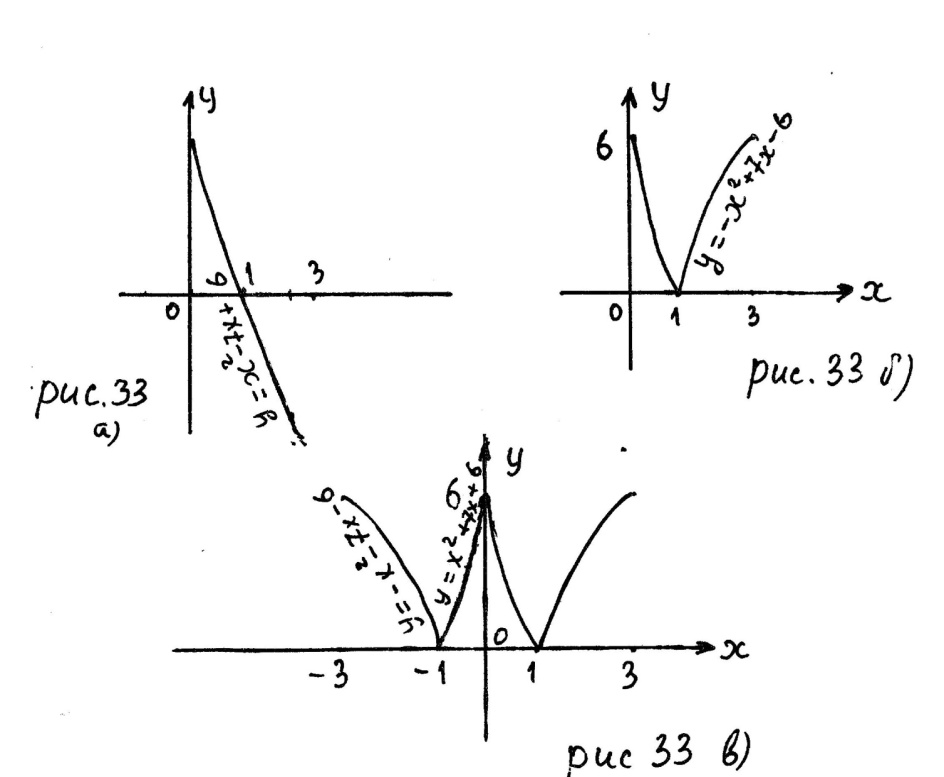3.
Построим график функции
,
которая является чётной периодической
функцией, с периодом
,
определённая на всей числовой прямой
и на отрезке
задана уравнением
.
а)
На рисунке 33 в) изображён график функции
на отрезке
(воспользовались тем, что функции
является чётной).
б)
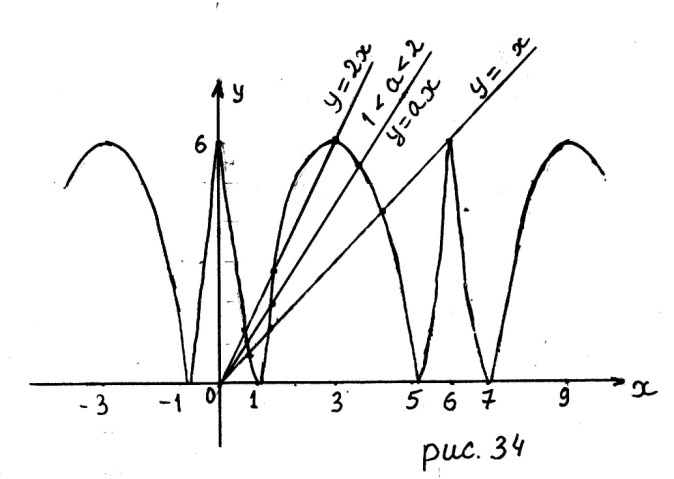
На рисунке 34 изображён график функции
на отрезке
(воспользовались тем, что функции
является периодической с периодом
).
Отметим: исходное уравнение имеет бесконечное множество корней, если и не имеет корней, если (рис. 34); не является корнем исходного уравнения.
Замечание.
Так как функции
является чётной, то, если пара
удовлетворяет уравнению
,
то и пары
также удовлетворяет этому уравнению.
Из
замечания следует, что исходное уравнение
надо рассмотреть при
и
Если при
и
исходное уравнение имеет три корня, то
при
и
это уравнение имеет шесть корней.
2. Исходное уравнение при и имеет три корня, если графики функций , пересекаются в трёх точках.
а)
Из рисунка 34 следует, что графики функций
,
при
пересекаются в одной точке, если
.
б)
Найдём число точек пересечения графиков
функций
,
,
где
,
если график функции
проходит через точку А(3;
6). Имеем
При
функция
принимает вид
.
Число
точек пересечения графиков функций
,
где
,
найдём из системы
Итак,
графики функций
,
,
если
пересекаются в двух точках.
Из а) и б) следует: если , то графики функций , , пересекаются в трёх точках.
б)
Найдём число точек пересечения графиков
функций
,
,
где
,
если график функции
проходит через точку А
(6;
6). Имеем
При
функция
принимает вид
.
Из
рисунка 34 следует, что графики функции
и
,
где
пересекаются в четырёх точках.
Из
рисунка 34 следует, если
и
,
то графики функций
,
пересекаются в трёх точках.
Отметим:
если
и
,
то графики функций
,
пересекаются более чем в трёх точках.
Из
замечания следует, что исходное уравнение
имеет шесть корней, если
.
Ответ. .
Упражнения.
1.
Сколько корней в зависимости от параметра
а
имеет уравнение
?
Найдите эти корни.
Ответ.
Если
,
то два корня
,
;
если
,
то два корня
,
.
2.
Найдите все значения параметра а,
при которых уравнение
имеет два корня. При
графическом методе надо обосновать,
что при
уравнение имеет два корня. Для этого
надо доказать, что имеет два корня
система
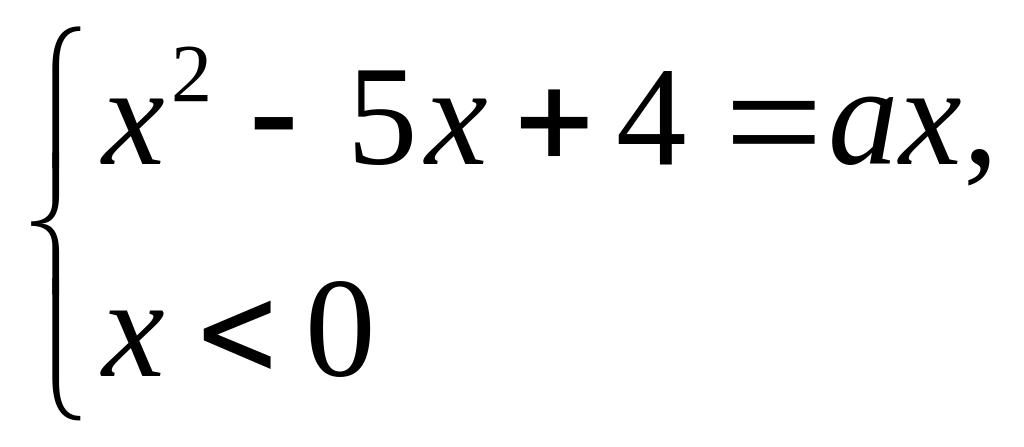
Ответ.
3.
Решите уравнение
.
Ответ.
При
уравнение имеет одно решение
при
решениями
уравнения являются
(уравнение
имеет бесконечное множество решений);
при
уравнение имеет одно решение
4.
Сколько решений в зависимости от
параметра а
имеет
уравнение
на отрезке
?
Ответ.
Если
,
то одно решение; если
,
то два решения.
5.
Найдите
все значения параметра
,
при которых уравнение
имеет единственный корень.
Ответ.
6.
Найдите
все значения параметра
,
при которых уравнение
имеет единственный корень.
Ответ.
7.
Найдите
все значения параметра
,
при которых уравнение
имеет единственный корень; имеет более
одного корня; не имеет корней.
Ответ.
8.
Найдите
все
значения параметра а,
при которых уравнение
не
имеет корней.
Ответ.
.
9. Найдите все значения параметра а, при которых уравнение
имеет
не менее двух решений.
Ответ.
.
10.
Найдите
все значения параметра а, при которых
уравнение
имеет два корня.
Ответ.
11.
Решите
уравнение
.
Ответ.
Если
,
то не имеет корней;
,
то два корня
,
;
если
,
то бесконечное множество корней, корнем
является любое
.
12.
Найдите все значения параметра а,
при которых уравнение
имеет четыре корня.
Ответ.
13.
Найдите
все значения параметров а
и b,
при которых уравнение
имеет единственный корень.
Ответ.
14.
Найдите все значения параметра а,
при которых уравнение
имеет три корня. Найдите эти корни.
Ответ.
Если
,
то три корня
,
,
.
15.
Найдите все значения параметра а, при
которых уравнение
имеет не менее четырёх различных решений,
являющихся целыми числами.
Ответ.
16.
Найдите все значения параметра а,
при которых уравнение
имеет два решения.
Ответ.
17.
Найдите все значения параметра а,
при которых уравнение
имеет 3 различных корня. Найдите эти
корни.
Ответ.
Если
то
;
если
то
.
18. Найдите все значения параметра а, при которых уравнение
имеет
бесконечное множество решений.
Ответ.
19.
Решите уравнение
.
Ответ.
Если
то
два
корня:
,
;
если
,
то
два
корня:
,
;
если
то четыре корня:
,
,
,
;
если
то три корня:
,
;
если
,
то два корня:
,
.
20. Найдите все значения параметра а, при каждом из которых
уравнение
имеет 1) один корень; 2) два корня. Найдите
эти корни.
Ответ.
1) Три
корня, если
,
то
,
,
если
,
то
,
2)
Два
корня, если
,
то
,
если
,
то
если
то
21.
Найдите
все значения параметра а,
при каждом из которых уравнение
имеет единственный корень.
Ответ.
22.
Найдите
все значения параметра а,
при каждом из которых уравнение
имеет три корня.
Ответ.
23.
Найдите
все значения параметра а,
при каждом из которых уравнение
имеет единственный корень.
Ответ.
или
24.
Сколько корней в зависимости от параметра
а
имеет уравнение
?
Ответ.
Если
то
4 корня;
если
то
3 корня;
если
то
2 корня;
если
то
1 корень;
если
то
корней
нет.
25.
Сколько корней в зависимости от параметра
а
имеет уравнение
?
Ответ.
Если
то
2
корня;
если
то
3 корня;
если
то
4 корня;
если
,
то
1
корень;
если
то
корней нет.
26.
Решите уравнение
.
Ответ.
Если
,
то корней нет;
если
,
то три корня:
;
если
,
то четыре корня:
если
,
то два
корня:
.
27. Найдите все значения параметра а, при которых уравнение
имеет
четыре корня.
Ответ.
28.
Найдите
все значения параметра а,
при каждом из которых уравнение
имеет ровно один корень.
Ответ.
29.
Найдите все значения параметра
,
при которых уравнение
имеет хотя бы одно решение, удовлетворяющее
условию
.
Ответ.
или
30.
Найдите все значения параметра а,
при которых уравнение
имеет
решения. Найдите эти решения.
Ответ.
Если
31.
Нечётная периодическая функция
,
с периодом
,
определённая на всей числовой прямой,
на отрезке
задана уравнением
.
Найдите все значения параметра а,
при которых уравнение
имеет ровно 6 корней.
Ответ.
32.
Найдите все значения параметра а,
при которых уравнения
и
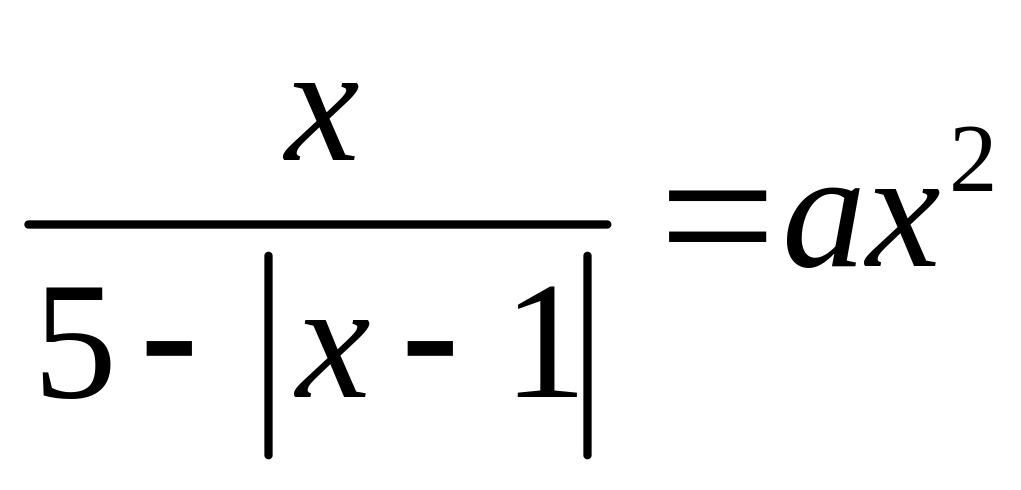имеют корни, причём число корней в этих
уравнениях одинаковое.
Ответ.
33.
При каких значениях k
уравнение
имеет
три корня?
Ответ.
34.
Найдите
все значения параметра а, при каждом из
которых уравнение
имеет один корень.
Ответ.
35.
Найдите все значения параметра а,
при которых уравнение
имеет четыре корня.
Ответ.
.
36.
Найдите
все значения параметра а,
при которых уравнение
имеет единственный корень.
Ответ.
