Подготовка к ЕГЭ

Задачи с параметрами

Уравнения с модулем

задачи типа заданий С 5

Дихтярь м.Б.

Общие сведения

1. Абсолютной величиной, или модулём числа х, называется само число х, если число , если ноль, если

При решении уравнения с модулем пользуемся тем, что

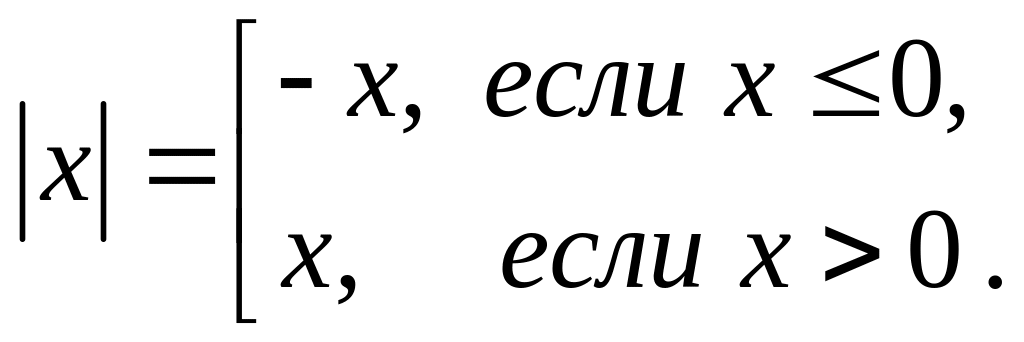
2. Построение графиков функций, содержащих модуль.

а) Построить график функции где

_{Решение. Имеем}

Графиком функции , где является «уголок» с вершиной в точке и сторонами

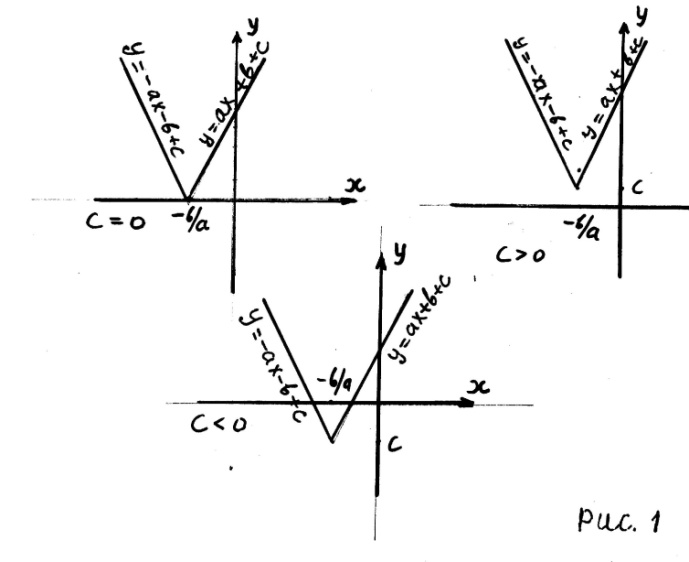
График функции , где схематично изображён на рисунке 1, для случая когда

б) Построить график функции где

_{Решение. Имеем}

Графиком функции , где , является «уголок» с вершиной в точке и со сторонами

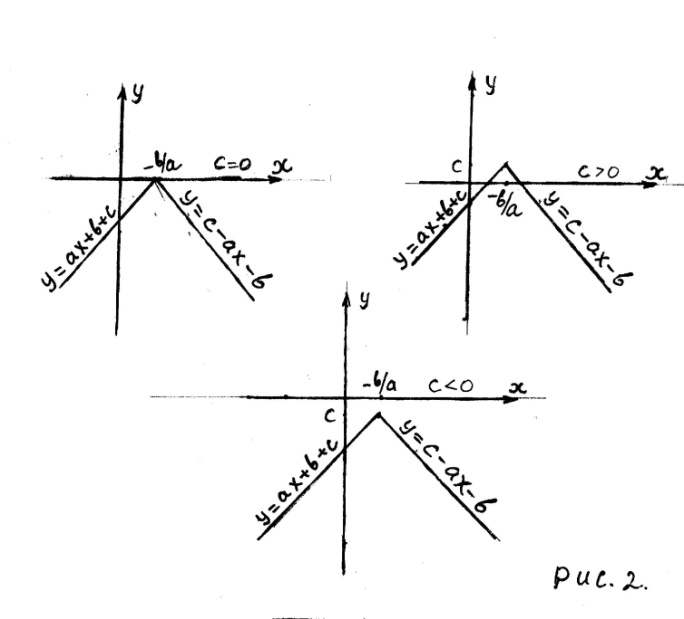
График функции , где , схематично изображён на рисунке 2, для случая когда

в) Построить график функции ^.

Решение. Найдём нули выражений, стоящих под знаком модуля:

Функция линейная на каждом промежутке , , . Для построения графика функции:

1) найдём значения функции в тех точках, в которых выражения, стоящие под знаком модуля равны нулю, а также в одной из точек, например, в точке , принадлежащей промежутку , и, например, в точке , принадлежащей промежутку . Имеем , ;

2) построим точки: (– 2; –1), (–1; 1), (2; 1), (3; 3);

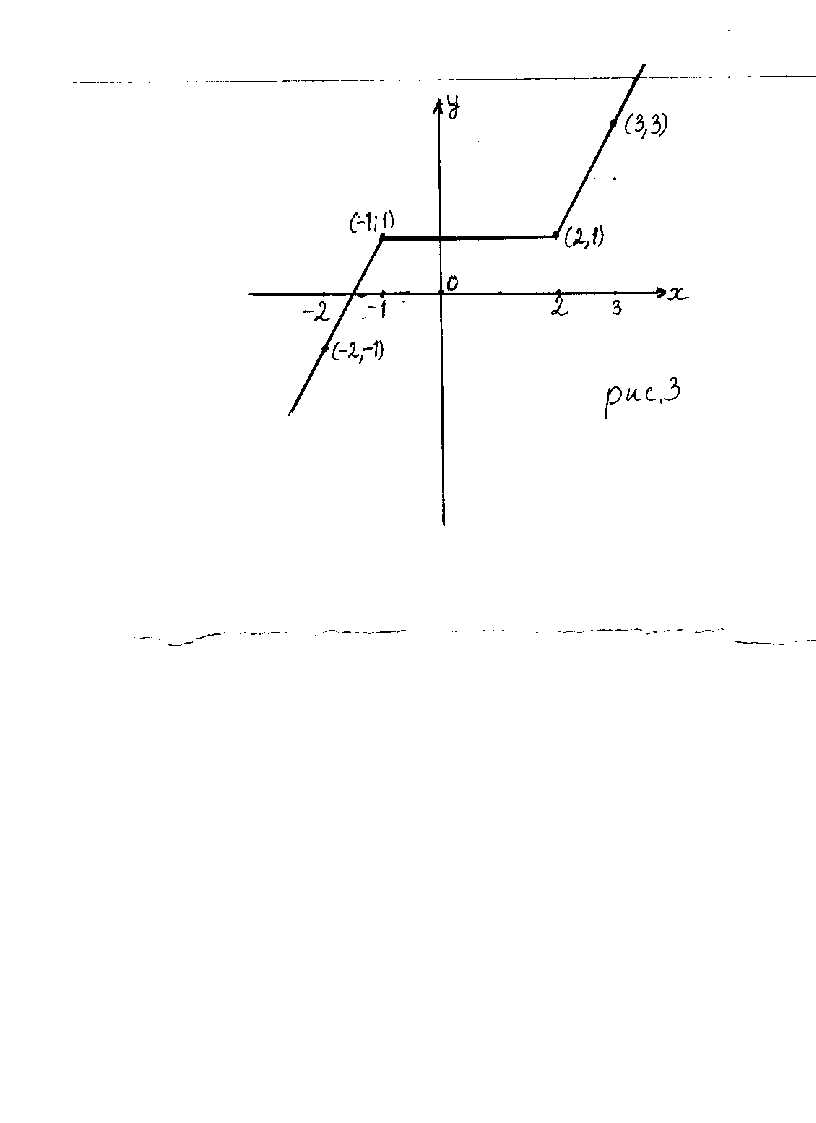
3) на каждом промежутке , , построим часть прямой (функция линейная на каждом промежутке), проходящей через точки, абсциссы которых принадлежат соответствующему промежутку.

График функции схематично изображён на рисунке 3.

г) Построить график функции .

Решение. 1. Найдём нули выражений, стоящих под знаком модуля:

Нули выражений, стоящих под знаком модуля:

2. Так как функция линейная на каждом промежутке , , , , , то для того чтобы построить график функции на каждом промежутке проделаем следующее.

1) Найдём значения функции в тех точках, в которых выражения, стоящие под знаком модуля равны нулю, а также в точках и .

Имеем .

2) На плоскости построим точки

3). На каждом промежутке , , , , построим часть прямой, проходящей через точки, абсциссы которых принадлежат соответствующему промежутку.

График функции схематично изображён на рисунке 4.

3. Построение графика функции .

График функции получается из графика функции следующим образом:

а) строим график ;

б) те точки графика, для которых , остаются без изменения, а точки графика, для которых отображаются относительно оси х.

4. Примеры

Построить графики функций

1) 2) 3)

Решения.

1) а) Имеем

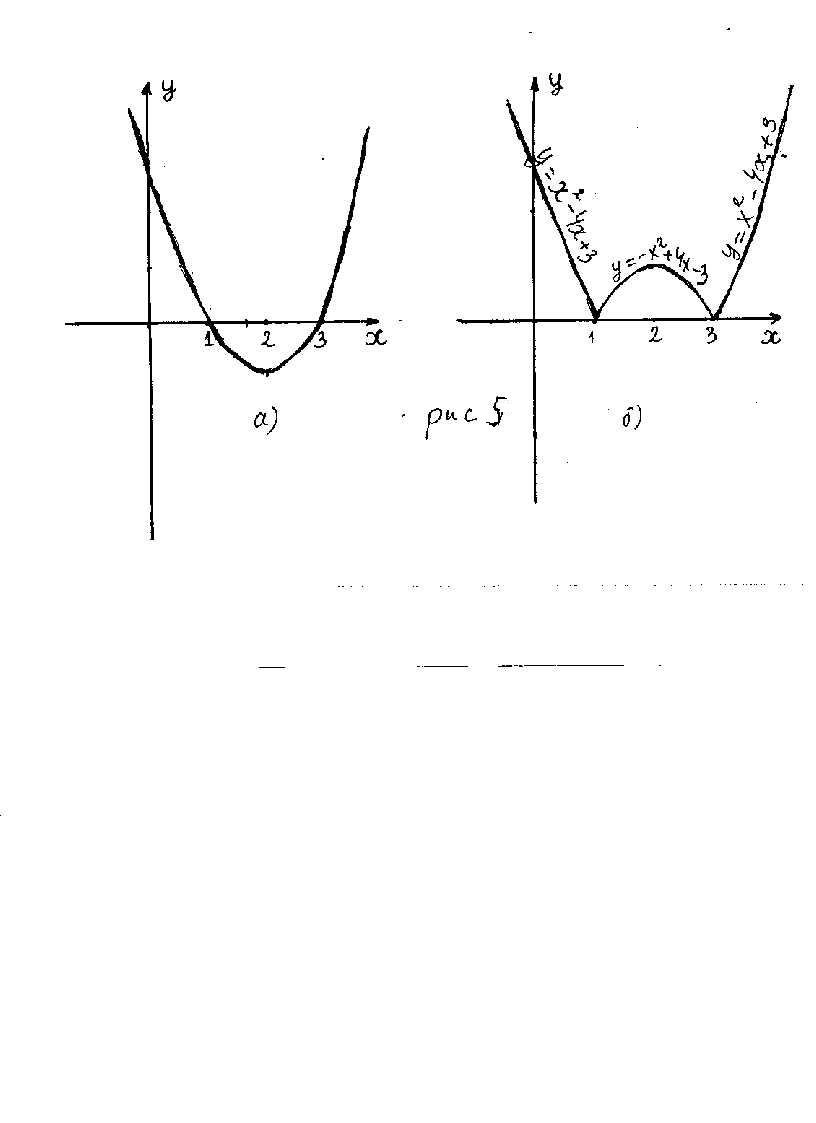Из последнего уравнения следует, что графиком функции является парабола с вершиной в точке (2; –1), ветви которой направлены вверх. Точки пересечения параболы с осью абсцисс находим из уравнения

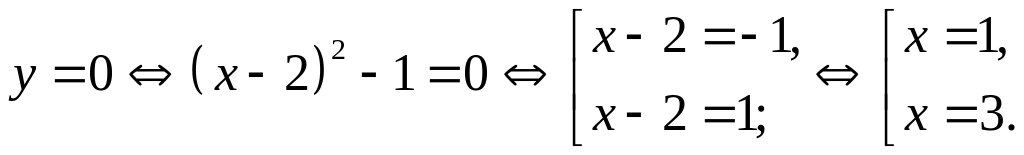Строим график параболы (рис. 5 а).

б) Строим график функции (рис. 5 б).

2) а) Имеем

Из последнего уравнения следует, что графиком функции является парабола с вершиной в точке (2; 1), ветви которой направлены вверх. Так как вершина параболы расположена выше оси абсцисс и её ветви направлены вверх, то парабола не пересекает ось абсцисс. Тогда .

Таким образом, имеем .

Графиком функции является парабола .

Замечание. Графиком функции является гипербола, асимптотами которой являются прямые

3)

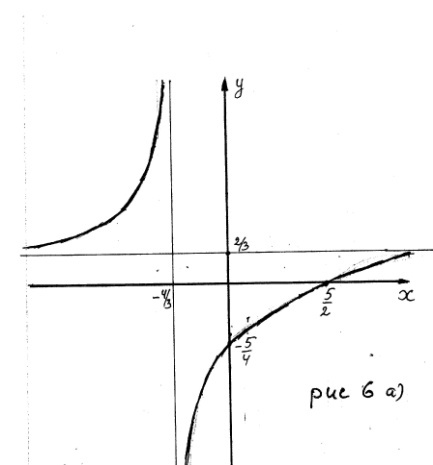
Имеем

Графиком функции 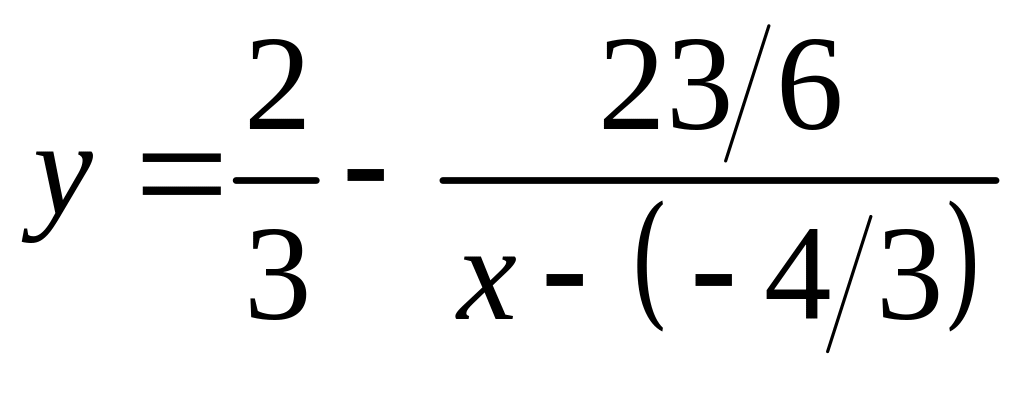является гипербола (рис. 6 а)), асимптотами которой являются прямые

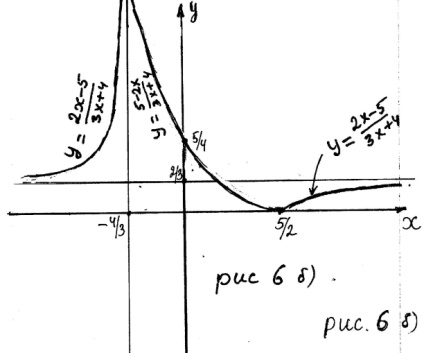
б) Строим график функции (рис. 6 б)).

Уравнения с модулем

Основные методы решения уравнений с модулем рассмотрим на примерах 1. – 3..

Метод интервалов

1. Сколько корней в зависимости от параметра а имеет уравнение ? Найдите эти корни.

Решение. 1. Приравняем нулю выражения, стоящие под знаком модуля: . Точки и разбивают числовую ось на три промежутка: .

2. Рассмотрим исходное уравнение на каждом промежутке.

Замечание. При раскрытии модуля надо учитывать знак выражения, стоящего под модулем на соответствующем промежутке. Так как знак выражения на каждом промежутке постоянный, то знак выражения на промежутке совпадает со знаком выражения в любой точке этого промежутка.

Раскрывая модули, заменим исходное уравнение равносильной совокупностью трёх уравнений:

а) Рассмотрим первое уравнение совокупности (1.1).

Корнем исходного уравнения на промежутке является , если

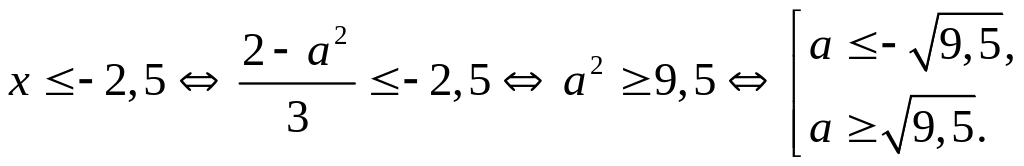
Итак, корнем исходного уравнения на промежутке является , если

б) Рассмотрим второе уравнение совокупности (1.1).

Корнем исходного уравнения на промежутке является , если

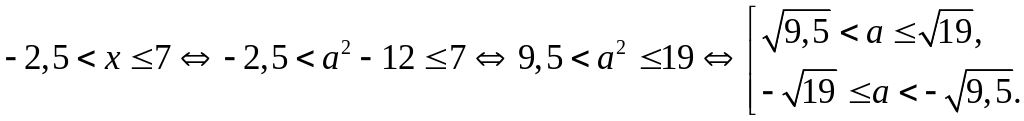
Итак, корнем исходного уравнения на промежутке является , если

в) Рассмотрим третье уравнение совокупности (1.1).

Корнем исходного уравнения на промежутке является

, если

Итак, корнем исходного уравнения на промежутке является , если

Нанесём корни уравнения на числовую прямую параметра (рис.7).

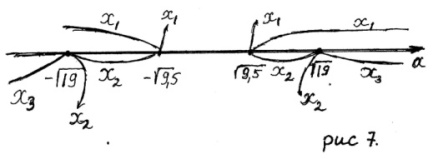Ответ. Если , то нет корней; если , то один корень ; если , то два корня , ; если , то два корня , .