
- •«Математические модели и методы исследования операций» Аснина а.Я., Аснина н.Г.
- •Тема 1. Оптимизация на сетях.
- •Построение математической модели.
- •Метод потенциалов для сетевой транспортной задачи.
- •Тема 2. Сети без контуров. Свойства сетей без контуров.
- •Задачи о кратчайшем и критическом пути.
- •Метод решения задач о кратчайшем и критическом пути.
- •Тема 3. Задачи, сводящиеся к задачам о кратчайшем и критическом пути. Задача о замене оборудования.
- •Задача оптимизации временной структуры проекта.
- •Тема 4. Теория расписаний. Общие положения
- •Задача о назначениях
- •Самостоятельная работа.
- •Система конвейерного типа с двумя приборами
- •Конвейерная система с тремя и более приборами
- •Самостоятельная работа.
- •Библиографический список
Самостоятельная работа.
Дана матрица С (рис. 4.16).
3 |
6 |
4 |
8 |
10 |
15 |
4 |
8 |
9 |
10 |
12 |
16 |
2 |
4 |
10 |
12 |
14 |
15 |
5 |
6 |
9 |
10 |
10 |
11 |
1 |
2 |
3 |
4 |
5 |
6 |
5 |
6 |
7 |
9 |
10 |
12 |
Рис. 4.16
Решить задачу о назначениях
Для каждого варианта в исходной матрице С вычеркнуть три элемента. Координаты вычеркиваемых элементов приведены на (рис.4.17)
Рис 4.17
Номер варианта |
Координаты |
Номер варианта |
Координаты |
Номер варианта |
Координаты |
Номер варианта |
Координаты |
1 |
(1,3);(2,1); (3,2) |
3 |
(1,3);(3,2); (5,6) |
5 |
(2,1);(3,2); (4,5) |
7 |
(2,1);(5,6); (6,4) |
2 |
(1,3);(2,1); (4,5) |
4 |
(1,3);(3,2); (6,4) |
6 |
(2,1);(3,2); (5,6) |
8 |
(3,2);(4,5); (5,6) |
Номер варианта |
Координаты |
Номер варианта |
Координаты |
Номер варианта |
Координаты |
Номер варианта |
Координаты |
9 |
(1,3);(2,1); (5,6) |
12 |
(1,3);(4,5); (5,6); |
15 |
(2,1);(3,2); (6,4) |
18 |
(3,2);(4,5); (6,4) |
10 |
(1,3);(2,1); (6,4) |
13 |
(1,3);(4,5); (6,4) |
16 |
(2,1);(4,5); (5,6) |
19 |
(3,2);(5,6); (6,4) |
11 |
(1,3);(3,2); (4,5) |
14 |
(1,3);(5,6); (6,4) |
17 |
(2,1);(4,5); (6,4) |
20 |
(4,5);(5,6); (6,4) |
21 |
(1,2);(2,1); (4,5) |
22 |
(1,2);(3,2); (4,5) |
23 |
(2,1);(1,3); (6,4) |
24 |
(2,1);(4,5); (6,6) |
Система конвейерного типа с двумя приборами
Постановка задачи:
Вербальная модель
Имеем n деталей, которые должны быть обработаны последовательно на первом и втором станках.
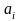 – время
обработки на первом станке,
– время
обработки на первом станке,
– время обработки на втором станке.
Требуется определить, в какой последовательности следует обрабатывать детали, чтобы выполнить эту работу за минимальное время.
Задача Джонсона
В сборном концерте должны выступать n артистов. Каждый из них должен готовиться к своему номеру в течение времени , а время пребывания артиста на сцене – . В гримерной одновременно может находиться один человек, так же как и на сцене. Требуется определить порядок выхода артистов на сцену, так чтобы время перерывов было минимально.
Вербальная модель Задачи Джонсона в терминах теории расписаний
Имеем n требований, каждое их которых должно быть последовательно обслужено на первом и втором приборах.
– время обслуживания i-го требования на 1-м приборе;
– время обслуживания i-го требования на 2-м приборе.
Требуется задать расписание обслуживания, минимизирующее общее время обслуживания.
Диаграмма Гантта.
Любое расписание для конвейерной системы можно представить в виде диаграммы Гантта.
Рассмотрим систему из трех требований, исходные данные для которой представлены на (рис.4.18)
Рис. 4.18
i |
1 |
2 |
3 |
|
1 |
1 |
3 |
|
2 |
1 |
2 |
Расписанию
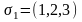 соответствует следующая диаграмма
Гантта (рис. 4.19):
соответствует следующая диаграмма
Гантта (рис. 4.19):

Рис. 4.19
На рис. 4.19 жирной линией показано время простоя, а Х – общее время обслуживания и Х=7.
Если
требования обслуживать в порядке
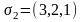 ,
то диаграмма Гантта будет иметь следующий
вид (рис. 4.20):
,
то диаграмма Гантта будет иметь следующий
вид (рис. 4.20):

Рис. 4.20
Общее время обслуживания Х=8.
Рис. 4.19-4.20 показывает, что длина расписания зависит от порядка обслуживания требований.
Вычисление длины расписания.
Пусть
задано расписание
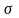 ,
введем обозначения:
,
введем обозначения:
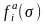 – момент
завершения обслуживания на первом
приборе требования, стоящего в расписании
на i-м
месте;
– момент
завершения обслуживания на первом
приборе требования, стоящего в расписании
на i-м
месте;
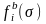 – момент
завершения обслуживания на втором
приборе требования, стоящего в расписании
на i-м
месте;
– момент
завершения обслуживания на втором
приборе требования, стоящего в расписании
на i-м
месте;
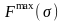 – длина
расписания
.
– длина
расписания
.
Так как требования обслуживаются последовательно, то длина расписания – это момент завершения обслуживания последнего требования на втором приборе, то есть
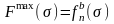 .
.
Из анализа диаграмм Гантта (см. рис.4.19 -4.20) получаем формулы для вычисления , :
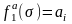 ,
,
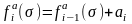 ,
,
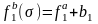 ,
,
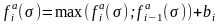 ,
,
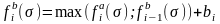 .
.
Пример 4.2. Дано пять деталей, которые последовательно обрабатываются на двух станках. Время обработки каждой детали на каждом станке указано на (рис.4.21)
Рис.4.21
i |
1 |
2 |
3 |
4 |
5 |
ai |
3 |
1 |
5 |
2 |
4 |
bi |
5 |
3 |
1 |
4 |
2 |
Если составить расписание обработки деталей в данном порядке, то получим (рис. 4.22)
Рис. 4.22
σ |
1 |
2 |
3 |
4 |
5 |
fia |
3 |
4 |
9 |
11 |
15 |
fib |
8 |
11 |
12 |
16 |
18 |
Здесь общее время обработки деталей составило 18.
Возьмем другое расписание: σ = (2,4,1,5,3), (рис. 4.23).
Рис. 4.23
σ |
2 |
4 |
1 |
5 |
3 |
fia |
1 |
3 |
6 |
10 |
15 |
fib |
4 |
8 |
13 |
15 |
16 |
Здесь общее время обслуживания равно 16.
Достаточное условие оптимальности расписания.
Теорема. Если в расписании для любого требования i предшествующего j выполняется условие
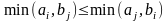 ,
(4.5)
,
(4.5)
то расписание оптимально.
Алгоритм построения расписания минимальной длины.
Условие (4.5) является достаточным для оптимальности расписания. То есть если для любой пары требований (i, j) из некоторого расписания условие (4.5) выполнено, то расписание оптимально. Однако строить оптимальное расписание с его помощью не слишком удобно, так как требуется большое количества проверок и переборов. Поэтому ниже будет предложен алгоритм построения расписания, удовлетворяющего условию (4.5), то есть являющегося оптимальным.
Алгоритм Джонсона
Шаг
1.
В первую группу заносятся требования,
у которых
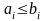 ;
во вторую группу заносятся требования,
у которых
;
во вторую группу заносятся требования,
у которых
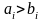 .
.
Шаг 2. Требования из первой группы сортируются по неубыванию аi и в таком порядке занимают первые место в расписании.
Шаг 3. Требования из второй группы сортируются по невозрастанию bi и занимают в таком порядке последующие места в расписании.
Пример 4.3. Дано пять деталей, которые последовательно обрабатываются на двух станках. Время обработки каждой детали на каждом станке указано на (рис.4.24)
Рис. 4.24
i |
1 |
2 |
3 |
4 |
5 |
ai |
3 |
1 |
5 |
2 |
4 |
bi |
1 |
3 |
2 |
4 |
5 |
В соответствии с требованиями алгоритма разобьем требования на группы (рис.4.25):
Рис. 4.25
I группа |
|
II группа |
|||||
|
|
|
|||||
i |
2 |
4 |
5 |
|
i |
1 |
3 |
ai |
1 |
2 |
4 |
|
bi |
1 |
2 |
Оптимальное
расписание
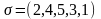 .
.
Длина расписания вычисляется на (рис.4.26)
Рис. 4.26
σ |
2 |
4 |
5 |
3 |
1 |
fia |
1 |
3 |
7 |
12 |
15 |
fib |
7 |
8 |
13 |
15 |
16 |
Здесь общее время обслуживания равно 16.
Доказательство оптимальности алгоритма Джонсона.
Докажем, что для расписания, полученного с помощью алгоритма Джонсона, выполнено условие (4.5).
В самом деле, пусть в расписании I предшествует j. Тогда возможны три случая
1) i,j ∊ I ,
2) i,j ∊ II ,
3) i ∊ I, j ∊ II .
??? Возможен ли случай когда j ∊ I, i ∊ II ?
Случай 1.
Если i и j принадлежат первой группе, то
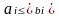 ,
(4.6)
,
(4.6)
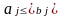 ,
(4.7)
,
(4.7)
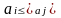 ,
(4.8)
,
(4.8)
Тогда
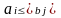 ,
откуда следует, что min(
,
откуда следует, что min(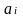 ;
;
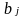 )
=
.
)
=
.
Чтобы доказать, что (4.5) выполнено нужно показать, что , . Но эти условия выполнены (4.6),(4.8).
???Задание для самостоятельной работы:
Докажите самостоятельно оптимальность алгоритма для второго случая. Подсказка: здесь будет выполнено min( ; ) = .
Случай 3.
В этом случае имеем
, (4.9)
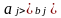 .
(4.10)
.
(4.10)
Так как требования из первой и второй группы не связаны никакими зависимостями, то min( ; ) может достигаться как на , так и на . Рассмотрим случай 3.1, где min( ; ) = , то есть
(4.11)
и требуется доказать что
(4.12)
(4.13)
(4.13)
следует из (4.9). Далее из (4.10) и (4.11) следует
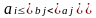 ,
то есть выполняется (4.12).
,
то есть выполняется (4.12).
???Задание для самостоятельной работы:
Самостоятельно доказать для случая (4.10), где min( ; ) = .
Замечание
о сложности алгоритма.
Поскольку алгоритм построения
оптимального расписания состоит из
сортировки, а сложность сортировки
имеет порядок
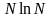 ,
то можно сказать, что задача Джонсона
с двумя приборами имеет
полимиальную сложность.
,
то можно сказать, что задача Джонсона
с двумя приборами имеет
полимиальную сложность.
