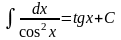Раздел 2. Основы математического анализа.

Группа	Дата
ОП-253	19.02.2014 21.02.2014
ОП-254	14.02.2014 21.02.2014

Тема 2.5 Неопределенный интеграл.

2.5.1. Основные понятия.

Определение. Функция F(x) называется первообразной функции f(x), если

Определение. Множество всех первообразных некоторой функции f(x) называется неопределенным интегралом функции f(x) и обозначается как

Таким образом, если F - некоторая частная первообразная, то справедливо выражение

где С - произвольная постоянная.

2.5.2. Свойства неопределенного интеграла.

В приведенных ниже формулах f и g - функции переменной x, F - первообразная функции f; а, k, C - постоянные величины.

Дифференциал от неопределенного интеграла равен подынтегральному выражению

_{Производная неопределенного интеграла равна подынтегральной функции:}

_{Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:}

_{Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых:}

_{Постоянный множитель можно выносить за знак интеграла:}

_{Инвариантность формулы интегрирования:}

2.5.3. Таблица основных интегралов.

В формулах ниже предполагается, что a, p (p ≠ 1), C - действительные постоянные, b - основание показательной функции (b ≠ 1, b > 0).

1		10
2		11
3		12
4		13
5		14
6		15
7		16
8		17
9		18

2.5.4. Методы интегрирования.

2.5.4.1.Метод непосредственного интегрирования

Метод непосредственного интегрирования является одним из основных методов.

Этот прием интегрирования применяется в том случае, если интеграл табличный или легко сводится к одному или нескольким табличным, путем использования свойств подынтегральной функции или следующих правил интегрирования:

1. ,

2. ,

где (х),  интегрируемые функции, k=const.

Пример 1. Найти .

Решение. Представляя интеграл от алгебраической суммы в виде суммы интегралов слагаемых, вынося постоянные множители за знаки интегралов и применяя формулы 1, 2 таблицы основных интегралов, получим

.

Замечание. Нет необходимости ставить произвольную постоянную после вычисления каждого интеграла, т.к. их сумма есть также произвольная постоянная, которую обозначают одной буквой и записывают в окончательный ответ.

Пример 2. Найти .

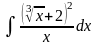Решение. Возведём двучлен в квадрат и запишем каждое слагаемое в виде степенной функции, затем, произведя почленное деление и применив формулы 2, 3 таблицы основных интегралов, получим

.

Пример 3. Найти .

Решение. Заменив единицу в числителе выражением sin²x+cos²x и почленно разделив числитель на знаменатель, получим

.

Пример 4. Найти .

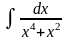Решение. Прибавим и вычтем х² в числителе подынтегральной функции, вынесем за скобки х² в знаменателе и почленно разделим числитель на знаменатель. Получим:

Пример 5. Найти .

Решение. Воспользуемся формулой тригонометрии . Тогда получим

.