1.2 Призначення матриць еталонних моделей [1]

Призначення матриць еталонних моделей засноване на використанні стандартних характеристичних поліномів. Ці поліноми забезпечують спеціальне розташування коренів характеристичного полінома системи на комплексній площині коренів. Прикладами таких поліномів є поліноми Ньютона (біноміальний) і Баттерворта.

1.2.1 Стандартні поліноми Ньютона [1]

Всі стандартні поліноми залежать від параметра [6]. Цей параметр визначає радіус розподілу коренів характеристичного полінома. Тому це значення завжди позитивно, тобто >0. Поліном Ньютона має наступний вигляд:

(1.17)

Поліноми Ньютони з першого по шостий порядок системи представлені в таблиці 1.1. Як видно з виразу (1.17), характеристичний поліпом має негативні дійсні кратні корені, які дорівнюють:

Таблиця 1.1 – Поліноми Ньютона

Порядок системи	Стандартний поліном Ньютона
1
2
3
4
5
6

Отже, такі корені забезпечують в системі аперіодичний характер перехідних процесів, тобто з нульовим перерегулюванням.

Зауваження 1.4 У реальних системах управління досягнення нульового значення перерегулювання є досить складним завданням. У багатьох випадках в системі присутнє перерегулювання, яке зумовлене інерційністю об'єкту управління.

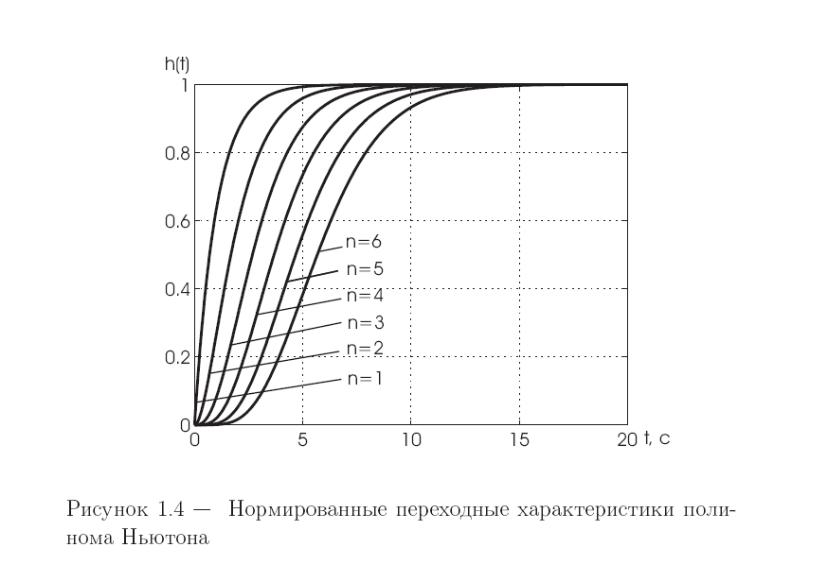
Значення порядку полінома. Вид, перехідної функції відповідає передавальній функції, у якої є тільки полюса і відносини вільних коефіцієнтів цих поліномів рівні 1. Нормовані перехідні функції виходять шляхом заміни значення параметра на одиницю в формулах, що визначають поліном Ньютона або Баттерворта при певному порядку полінома. Графіки нормованих перехідних функцій для випадку полінома Ньютона представлені на малюнку 1.4.

1.2.2 Стандартні поліноми Баттерворта [1]

У стандартному поліномі Баттерворта всі корені розподілені в лівій півплощині комплексної площині коренів на півколі з радіусом . Причому кут між сусідніми радіус - векторами коренів складає , а кут між ближніми радіус - векторами і уявною віссю дорівнює .

Тому корені такого полінома знаходяться за формулою :

Поліном Баттерворта виражається наступним чином :

Поліноми Баттерворта з першого по шостий порядок представлені в таблиці 1.2.

Нормовані перехідні функції для випадку полінома Баттерворта представлені на малюнку 1.5. Як видно з цього малюнка, перерегульовання нормованих стандартних перехідних функцій становить менше 20 %

Таблиця 1.2 - Поліноми Баттерворта

Порядок системи	Стандартний поліном Баттерворда
1
2
3
4
5
6

[1] – В.В.Григорьев, Н.В.Журавлева, Г.В.Лукьянова, К.А.Сергеев. Синтез систем автоматического управления. С-Пб: СПбГУ ИТМО, 2007. – 108 с. Ил.

[2] – В.А.Бесекерский, Е.П.Попов. Теория систем автоматического управления. С-Пб: «Профессия»

7