
- •Вопрос 2. Геодезические разбивочные работы: основные и детальные. Нормы точности разбивочных работ. Способы разбивки осей. Способы выноса плановых точек в натуру.
- •Вопрос 3. Составление плана организации рельефа. Способы перенесения в натуру проектных отметок, линий и плоскостей с заданным уклоном.
- •Вопрос 4. Разработка проекта производства геодезич. Разбивоч. Работ. Методы подготовки данных для перенесения проекта сооружений (в плановом положении) в натуру. Составление разбивочных чертежей.
- •Вопрос 5. Трассирование линейных сооружений. Камеральное и полевое трассирование. Беспикетное трассирование. Разбивка круговых кривых. Составление плана и профиля трассы.
- •Вопрос 7 Высотные инженерно геодезические сети.
- •Вопрос 8. Крупно масштабные инж-топогр съёмки застр. Территорий. Виды планов, методы их создания. Цифровые модели местности. Основные направления автоматизации крупномасштабных съёмок.
- •Вопрос 9. Выбор технологических осей, их закрепление, маркирование конструкций при установке технологического оборудование в проектное положение.
- •Вопрос 10 Геодезические способы, приборы и оборудование для плановой установки и выверки конструкции(струнный, струнно-оптический, оптического визирования, коллиматорный , дифракционный).
- •Вопрос 11. Геодезические способы, приборы и оборудование для установки конструкций по высоте. Геометрическое нивелирование короткими лучами, гидростатическое нивелирование, микронивелирование.
- •Вопрос 12. Геодезические способы для установки и выверки конструкций по вертикали. Прямые и обратные отвесы, способ наклонного визирования, способ оптического и вертикального проектирования.Ч
- •Вопрос 13. Исполнительные съемки и составление исполнительных генеральных планов. Виды исполнительных съемок. Геодезическая основа и методы исполнительных съемок сооружений и оборудования.
- •Вопрос15 Проектирование схем геодезического контроля общих осадок, размещения киа, принципы проектирования схем контроля, расчет точности геометрического нивелирования
- •Вопрос 16. Проектирование схем геодезического контроля кренов сооружений. Объекты контроля, точность, методы и средства измерений
- •Вопрос 17 Порядок проектирования. Выбор методов и средств измерений при контроле осадок и деформаций сооружений.
- •Вопрос 19 Методы и средства измерения горизонтальных смещений инженерных сооружений. Размещение киа, точность, цикличность измерений, створные методы, методы угловых и линейных измерений.
- •Вопрос 22 Геодезическое обеспечение проектирования, строительства железных и автомобильных дорог. Разбивочные работы. Разбивка стрелочных переводов, соединений и парков.
- •Вопрос 28 Назначение планового и высотного обоснования тоннелей. Виды планового обосн на поверхн и в подзем выработке. Расчет точности тонельной триангуляции, основной и поземной полигонометрии.
- •Вопрос 29. Высотное обоснование тоннелей. Расчёт точности высотного обосновая тоннелей. Передача отметок в подземные выработки.
- •Вопрос 30. Назначение и способы ориентирования подземной полигонометрии. Исследование наивыгоднейшей формы соединительного треугольника.
- •Вопрос 32. Основные понятия о гидротехнических сооружениях. Типы гэс. Геодезические работы на разных стадиях проектирования гидротехнических сооружений.
- •Вопрос 32. Типы, элементы и основные характеристики водохранилищ. Плановое и высотное обоснование водохранилища. Вынос контура водохранилища в натуру сооружений.
- •Вопрос 34. Основные оси сооружений гидроузла. Способы выноса основных осей в натуру. Плановое и высотное обоснование гидроузла в период строительства. Ступени создания планового обоснования.
- •Вопрос 41 Методы автоматизации геодезических измерений (створные измерения, контроль прямолинейности, строительно-монтажные работы, наблюдения за осадками)
- •Вопрос 48 Технология коррелатной версии метода наименьших квадратов – уравнивения геодезических измерений.
- •Вопрос 49. Технология параметрической версии мнк –уравнивания геод измерений.
- •Вопрос 50. Ско результата измерений и функции измеренных величин.
- •Вопрос 53 Общеземные и референцные координаты. Формулы связи между ними Необходимость перехода к системе референцных координат при использовании gps.
- •Вопрос 54 Проекция и плоские прямоугольные координаты Гауса-Крюгера, её свойства достоинства, недостатки. Необходимость применения ппкс частным началом.
- •Вопрос 57 Устройство оптических систем зрительной трубы и оптические устройства теодолитов типа т2 или т5. Основные неисправности оптических систем теодолитов.
Вопрос 50. Ско результата измерений и функции измеренных величин.
В геодезии искомые величины находят вычислениями как функции измеренных величин. Ошибка функции зависит от ошибок аргументов, по которым она вычислена, и от вида функции. Истинные ошибки измеренных аргументов остаются неизвестными, и истинные ошибки функции могут быть найдены лишь в случаях, когда известна теоретическая величина функции (сумма углов треугольника). В этих случаях ошибку функции м получить как разность между величиной функции, вычисленной с измеренными значениями аргумента, и ее теоретической величиной. Эта разность наз. невязкой.
При вычислении СКО функции по известным СКО аргументов могут встретиться 2 случая: коррелированные и некоррелированные аргументы. Две или несколько случайных величин называют коррелированными, если коэффициенты корреляции парной статистической связи не равны нулю; в противном случае они некоррелированные.
Пусть дана функция
F=f(x,y,z.....u),
где x,y,z...u
– коррелированные аргументы, полученные
из наблюдений с СКО mx,
my,....,mu
соответственно. Предположим что X,
Y,
Z,...,U
– истинные значения аргументов.
Необходимо определить СКО mF
функции F.
Пусть Θx
Θy
Θz...Θu
– истинные ошибки аргументов, т.е.![]() ,
тогда истинная ошибка функции будет
,
тогда истинная ошибка функции будет
![]()
![]() Определим
СКО функции через математическое
ожидание квадрата ее истинной ошибки,
т.е.
Определим
СКО функции через математическое
ожидание квадрата ее истинной ошибки,
т.е.
![]()
![]()
![]() Значения
производных по соответствующим аргументам
практически остаются постоянными и
могут быть вычислены по приближенным
значениям аргументов x0,
y0,
z0...u0,
в качестве которых можно взять любые
результаты измерений.
Значения
производных по соответствующим аргументам
практически остаются постоянными и
могут быть вычислены по приближенным
значениям аргументов x0,
y0,
z0...u0,
в качестве которых можно взять любые
результаты измерений.
Из корреляционного анализа известно что коэффициент корреляции
![]()
![]()
![]() Окончательно
имеем:
Окончательно
имеем:
![]()
![]()
Для практического использования формулы коэффициенты корреляции должны быть определены из специальных исследований.
При организации наблюдений одно из основных требований – обеспечение таких условий при которых результаты многократных измерений одной и той же величины или разных величин, по возможности, были бы между собой независимыми. Любая методика геодезических измерений в той или иной мере рассчитана на выполнение этого требования.
Т.к. для некоррелированных аргументов коэффициенты корреляции равны нулю, то
![]() Т.о.,
СКО функции некоррелируемых аргументов
равна корню квадратному из суммы
квадратов произведений частных
производных функций по каждому из
аргументов на СКО соответствующих
аргументов.
Т.о.,
СКО функции некоррелируемых аргументов
равна корню квадратному из суммы
квадратов произведений частных
производных функций по каждому из
аргументов на СКО соответствующих
аргументов.
Bопрос 51. Геодезические и нормальные высоты и связь между ними, их геометрическая интерпретация и области применения. Понятие о системе геопотенциальных высот.
В ысота
точек земной поверхности Н – одна из
координат, определяющих фигуру Земли
и отдельные её точки относительно
исходной отсчётной поверхности. Высота
Нм
определяет отстояние точки М от
эллипсоида по нормали к нему. высоты
всех точек Земли определяют фигуру
физической поверхности Земли относительно
принятого референц-эллипсоида. Разность
высот точек земной поверхности, получаемые
из нивелирования, определяют разность
потенциалов силы тяжести между этими
точками. Если известно значение потенциала
W0
в исходном футштоке, то в результате
нивелирования легко вычислить значение
потенциалов силы тяжести в соответствующих
точках поверхности Земли по известной
формуле
ысота
точек земной поверхности Н – одна из
координат, определяющих фигуру Земли
и отдельные её точки относительно
исходной отсчётной поверхности. Высота
Нм
определяет отстояние точки М от
эллипсоида по нормали к нему. высоты
всех точек Земли определяют фигуру
физической поверхности Земли относительно
принятого референц-эллипсоида. Разность
высот точек земной поверхности, получаемые
из нивелирования, определяют разность
потенциалов силы тяжести между этими
точками. Если известно значение потенциала
W0
в исходном футштоке, то в результате
нивелирования легко вычислить значение
потенциалов силы тяжести в соответствующих
точках поверхности Земли по известной
формуле![]() или
или
![]() Область
применения.
Высоты нужно знать для решения следующих
задач:1,для определения фигуры земли.
2,для изображения
рельефа на топокартах.3,для редуцирования
результатов измерений с физ. поверх.
земли на поверх. модели (эллипсоид).4,При
проектировании и строительстве инж.
сооружений и решении других проектировочных
задач, в которых нужно знать взаимное
пространственное положение.
5,для связи
геодезической системы координат и
прямоугольной пространственной системы
координат.Геод-ие
высоты Н
-сумма двух слагаемых: расстояния от
референц-эллипсоида до поверхности
геоида, или квазигеоида и расстояния
от одной из этих поверхностей до
соответствующей точки поверхности
Земли.Оба указанных выше слагаемых
должны быть отрезками нормали к
поверхности референц-эллипсоида.
Исслед-ия Молоденского показали, что
могут быть вычислены точно оба слагаемых
Нм
–
нормальная высота
и м-
аномалия
высоты,
высота квазигеоида над поверхностью
референц-эллипсоида. Поэтому для
вычисления геодезических высот Н в
настоящее время применяется формула
Нм=
Нм+м,
предусматривающая использование системы
нормальных высот
Н
и аномалий высот .
Расчленение высоты Н на два слагаемых
вызывается практической необходимостью
иметь высоты
от уровня моря.
Принятие поверхности «уровня
моря» в
качестве отсчётной поверхности для
высот, используемых на практике, имеет
определённый физический смысл, который
заключается в том, что за исходную
поверхность принимается уровенная
или горизонтальная
поверхность
или поверхность, весьма близкая к ней.
При вычислении высот практически
приходится иметь дело с двумя отсчётными
поверхностями: 1) референц-эллипсоида
для вычисления геодезических высот Н,
определяющих по высоте точки земной
поверхности, и 2) квазигеоида для
вычисления нормальных высот, используемых
в практических расчётах и показываемых
на картах при изображении топографического
рельефа. Приращение
потенциала силы тяжести в данной точке
относительно начального футштока,
взятое с обратным знаком, называется
геопотенциалом.Следует
иметь в виду, что главной характеристикой
высоты репера является именно геопотенциал,
как непосредственно измеренная величина,
а не какие либо расстояния от данной
точки до некоторых воображаемых
поверхностей.Существует
четыре системы геопотенциальных
высот:
приближённые,
ортометрические, нормальные и
динамические.Приближённые высоты
получаются,
если не принимать во внимание реальное
гравитационное поле силы тяжести Земли.К
вычислению приближённых высот приходится
прибегать в том случае, если вдоль линии
нивелирования не производились измерения
силы тяжести, выявляющие влияние
действительного поля силы тяжести
Земли; вычисления высот в других системах.
Из определения высот следует, что
измеренные величины Низм
следует исправить только за непараллельность
уровенных поверхностей нормального
поля. Ортометрические
высоты
(это отрезок отвесной линии, заключённый
между физической поверхностью земли и
поверхносьью геоида HgM)
имеют крупный недостаток принципиального
характера – они не могут быть вычислены
точно, из-за зависимости от распределения
плотностей внутри Земли, которые в
настоящее время неизвестны. В этом
случае точность вычисления будет
зависеть от степени достоверности
применённой гипотезы строения Земли.
Вследствие этого не представляется
возможным в полной мере оценить точность
получаемых высот Нg.Нормальные
высоты (это
отрезок нормали к эллипсоиду, заключённый
между физической поверхностью земли и
поверхностью квазигеоида HƔM).
Нормальная высота определяется независимо
от пути нивелирования. Точки, расположенные
на одной уровенной поверхности, в общем
случае будут иметь различные высоты, в
частном случае при расположении точек
на одной параллели высоты будут
одинаковыми. По измеренной разности
действительных потенциалов силы тяжести
вычисляют высоты, но в нормальном
гравитационном поле Земли, не принимая
во внимание возмущающего потенциала и
связанных с ним величин аномалий силы
тяжести или уклонений отвесной линии.
Следствием этого получается несовпадение
геодезической высоты Нм
с нормальной Нм
на величину =Нм-
Нм
которая таким образом, получает смысл
аномалии
высоты.Ошибка
вычислений Нм
и
зависит только от ошибок непосредственных
измерений. В
этом состоит главное и важное преимущество
нормальных высот перед ортометрическими.
На поверхности океанов геоид и квазигеоид
совпадают, а аномалии высот выражают
высоту геоида или квазигеоида над
поверхностью уровенного эллипсоида.
Динамические
высоты.Обычно
считают, например, что точки земной
поверхности, имеющие одинаковые отметки,
находятся «на одном уровне» и соответственно
ведут свои расчёты при разработке
проектов тех или иных строительств.
Можно предположить, что влияние
непараллельности уровенных поверхностей
мало, а потому пренебрегаемо. Это,
конечно, справедливо во многих случаях
и, например, при топографических съёмках
непараллельность уровенных поверхностей
не учитывается. Но когда точность
определения высот имеет важное значение
(при строительстве больших гидротехнических
комплексов) и для проектирования
используются числовые
данные (в
отличие от графических), то эти
обстоятельства в необходимых случаях
следует учитывать. Динамические высоты
значительно отличаются от нормальных
или ортометрических высот по мере
удаления от параллели 450.
Эти различия могут достигать 10—20
м.Поскольку значение потенциала вполне
характеризует положение точки по высоте,
можно условиться находить высоту как
разность потенциалов, делённую на
некоторое постоянное значение силы
тяжести. Такие высоты при перемещении
точки по уровенной поверхности не
изменяются и называются динамическими
высотами
Нd.
При этом за постоянное значение силы
тяжести принимают значение нормальной
силы тяжести на широте
= 450.
Область
применения.
Высоты нужно знать для решения следующих
задач:1,для определения фигуры земли.
2,для изображения
рельефа на топокартах.3,для редуцирования
результатов измерений с физ. поверх.
земли на поверх. модели (эллипсоид).4,При
проектировании и строительстве инж.
сооружений и решении других проектировочных
задач, в которых нужно знать взаимное
пространственное положение.
5,для связи
геодезической системы координат и
прямоугольной пространственной системы
координат.Геод-ие
высоты Н
-сумма двух слагаемых: расстояния от
референц-эллипсоида до поверхности
геоида, или квазигеоида и расстояния
от одной из этих поверхностей до
соответствующей точки поверхности
Земли.Оба указанных выше слагаемых
должны быть отрезками нормали к
поверхности референц-эллипсоида.
Исслед-ия Молоденского показали, что
могут быть вычислены точно оба слагаемых
Нм
–
нормальная высота
и м-
аномалия
высоты,
высота квазигеоида над поверхностью
референц-эллипсоида. Поэтому для
вычисления геодезических высот Н в
настоящее время применяется формула
Нм=
Нм+м,
предусматривающая использование системы
нормальных высот
Н
и аномалий высот .
Расчленение высоты Н на два слагаемых
вызывается практической необходимостью
иметь высоты
от уровня моря.
Принятие поверхности «уровня
моря» в
качестве отсчётной поверхности для
высот, используемых на практике, имеет
определённый физический смысл, который
заключается в том, что за исходную
поверхность принимается уровенная
или горизонтальная
поверхность
или поверхность, весьма близкая к ней.
При вычислении высот практически
приходится иметь дело с двумя отсчётными
поверхностями: 1) референц-эллипсоида
для вычисления геодезических высот Н,
определяющих по высоте точки земной
поверхности, и 2) квазигеоида для
вычисления нормальных высот, используемых
в практических расчётах и показываемых
на картах при изображении топографического
рельефа. Приращение
потенциала силы тяжести в данной точке
относительно начального футштока,
взятое с обратным знаком, называется
геопотенциалом.Следует
иметь в виду, что главной характеристикой
высоты репера является именно геопотенциал,
как непосредственно измеренная величина,
а не какие либо расстояния от данной
точки до некоторых воображаемых
поверхностей.Существует
четыре системы геопотенциальных
высот:
приближённые,
ортометрические, нормальные и
динамические.Приближённые высоты
получаются,
если не принимать во внимание реальное
гравитационное поле силы тяжести Земли.К
вычислению приближённых высот приходится
прибегать в том случае, если вдоль линии
нивелирования не производились измерения
силы тяжести, выявляющие влияние
действительного поля силы тяжести
Земли; вычисления высот в других системах.
Из определения высот следует, что
измеренные величины Низм
следует исправить только за непараллельность
уровенных поверхностей нормального
поля. Ортометрические
высоты
(это отрезок отвесной линии, заключённый
между физической поверхностью земли и
поверхносьью геоида HgM)
имеют крупный недостаток принципиального
характера – они не могут быть вычислены
точно, из-за зависимости от распределения
плотностей внутри Земли, которые в
настоящее время неизвестны. В этом
случае точность вычисления будет
зависеть от степени достоверности
применённой гипотезы строения Земли.
Вследствие этого не представляется
возможным в полной мере оценить точность
получаемых высот Нg.Нормальные
высоты (это
отрезок нормали к эллипсоиду, заключённый
между физической поверхностью земли и
поверхностью квазигеоида HƔM).
Нормальная высота определяется независимо
от пути нивелирования. Точки, расположенные
на одной уровенной поверхности, в общем
случае будут иметь различные высоты, в
частном случае при расположении точек
на одной параллели высоты будут
одинаковыми. По измеренной разности
действительных потенциалов силы тяжести
вычисляют высоты, но в нормальном
гравитационном поле Земли, не принимая
во внимание возмущающего потенциала и
связанных с ним величин аномалий силы
тяжести или уклонений отвесной линии.
Следствием этого получается несовпадение
геодезической высоты Нм
с нормальной Нм
на величину =Нм-
Нм
которая таким образом, получает смысл
аномалии
высоты.Ошибка
вычислений Нм
и
зависит только от ошибок непосредственных
измерений. В
этом состоит главное и важное преимущество
нормальных высот перед ортометрическими.
На поверхности океанов геоид и квазигеоид
совпадают, а аномалии высот выражают
высоту геоида или квазигеоида над
поверхностью уровенного эллипсоида.
Динамические
высоты.Обычно
считают, например, что точки земной
поверхности, имеющие одинаковые отметки,
находятся «на одном уровне» и соответственно
ведут свои расчёты при разработке
проектов тех или иных строительств.
Можно предположить, что влияние
непараллельности уровенных поверхностей
мало, а потому пренебрегаемо. Это,
конечно, справедливо во многих случаях
и, например, при топографических съёмках
непараллельность уровенных поверхностей
не учитывается. Но когда точность
определения высот имеет важное значение
(при строительстве больших гидротехнических
комплексов) и для проектирования
используются числовые
данные (в
отличие от графических), то эти
обстоятельства в необходимых случаях
следует учитывать. Динамические высоты
значительно отличаются от нормальных
или ортометрических высот по мере
удаления от параллели 450.
Эти различия могут достигать 10—20
м.Поскольку значение потенциала вполне
характеризует положение точки по высоте,
можно условиться находить высоту как
разность потенциалов, делённую на
некоторое постоянное значение силы
тяжести. Такие высоты при перемещении
точки по уровенной поверхности не
изменяются и называются динамическими
высотами
Нd.
При этом за постоянное значение силы
тяжести принимают значение нормальной
силы тяжести на широте
= 450.
В опрос
52. геодезические и астрономические
координаты и азимуты, соотношения между
ними. Уклонение отвесных линий.
опрос
52. геодезические и астрономические
координаты и азимуты, соотношения между
ними. Уклонение отвесных линий.
 А
А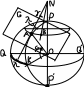
 строномические
координаты.Положение
точки на поверхности сферы определяется
двумя сферическими координатами –
широтой и долготой (О-центр сферы; точка
Р-северный полюс; точка Р’-южный полюс).
Проведём линию экватора QQ’
полученную от пересечения плоскости
экватора и поверхности сферы.
Широта
φ точки А – это
угол,
образованный
отвесной линией точки А и плоскостью
экватора;
этот угол лежит в плоскости меридиана
точки. Широта
отсчитывается в обе стороны от экватора
(к северу – северная широта, к югу –
южная) и изменяется от 00
до 900.Долгота
точки λ - это
двугранный угол между плоскостью
начального меридиана и плоскостью
астрономического меридиана точки А.
Начальный меридиан проходит через центр
главного зала Гринвичской обсерватории,
расположенной вблизи Лондона. Плоскость
астрономического меридиана – плоскость,
проходящая через отвесную линию в данной
точки и распологающуюся параллельно
оси вращения земли. Долготы изменяются
от 00 до
1800,
к западу от Гринвича – западные и к
востоку – восточные. Все точки одного
меридиана имеют одинаковую долготу.
Проведём плоскость G,
касательную к поверхности сферы в точке
А;
эта плоскость называется плоскостью
горизонта точки А.
Линия пересечения плоскости горизонта
и плоскости меридиана точки называется
полуденной
линией ;
направление полуденной линии – с юга
на север. Если провести полуденные линии
двух точек, лежащих на одной параллели,
то они пересекутся в точке на продолжении
оси вращения Земли PP’
и образуют угол ,
который называется сближением меридианов
этих точек. Широту
и долготу точек местности определяют
из астрономических наблюдений, потому
они и называются астрономическими
координатами. Астрономические наблюдения
в общем случае заключаются в
измерении:1,зенитных расстояний светил,2,
измерении соответствующих горизонтальных
углов,3,фиксации моментов времени этих
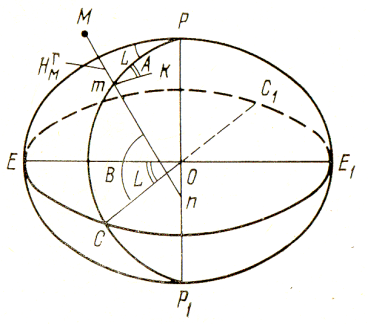
измерений по часам.Геодезические
координаты.
На поверхности эллипсоида вращения
положение точки определяется геодезическими
координатами – геодезической широтой
В,
геодезической долготой L
и геодезической высотой НГ.
Геодезическая
широта В точки М –
это угол, образованный нормалью Mn
к поверхности эллипсоида в этой точке
и плоскостью экватора ЕСЕ1.
Геодезические широты отсчитываются от
плоскости экватора к северному полюсу
со знаком плюс, а к южному полюсу – со
знаком минус, от 0º до 90º
Геодезическая
долгота L
точки М– это
двугранный угол между плоскостью PEP1
начального меридиана (гринвический) и
плоскостью PmP1
меридиана данной точки M.
Плоскость
геодезического меридиана проходит
через точку M
и малую полуось эллипсоида; в этой
плоскости лежит нормаль к поверхности
эллипсоида в точке M.
Геодезическая параллель получается от
пересечения поверхности эллипсоида
плоскостью, проходящей через точку M
и параллельной плоскости экватора.
Различие
геодезических и астрономических
координат
точки M
зависит от угла между отвесной линией
данной точки и нормалью к поверхности
эллипсоида в этой же точке. Этот угол
называется уклонением отвесной линии;
он обычно не превышает 5”. В некоторых
районах Земли, называемых аномальными,
уклонение отвесной линии достигает
нескольких десятков дуговых секунд.
При геодезических работах невысокой
точности астрономические и геодезические
координаты не различают; их общее
название – географические координаты
– используется довольно часто. Широта:
северная или южная 0≤B≤90º.
Долгота:
западная или восточная 0≤L≤180º
. Через
уклонение отвесных линий устанавливается
простая связь между астрономическими
и геодезическими координатами. Это
позволяет, зная уклонения отвесных
линий, переходить от астрономических
координат
и
к геодезическим В и L
при помощи формул: В=+,
L=+
}, где
и
- весьма простые функции слагающих
уклонений отвесных линий в меридиане
и первом вертикале. Это соотношение
имеет и другое принципиальное значение:
если оба слагаемых правой части вывести
из измерений, то тем самым можно определить
две координаты точек поверхности Земли,
изучение которой составляет главную
задачу высшей геодезии. Возможность
перехода координат крайне важна, в
частности при использовании астрономических
пунктов как опорных, при топографических
съёмках.Астрономический
азимут αмk
– называется угол между плоскостью
астрономического меридиана в данной
точке М и вертикальной плоскостью,
проходящей через точку k.
Геодезический
азимут Амk
– двугранный угол Pmk
в точке m,
образованный плоскостью геодезического
меридиана PmP1
данной точки и нормальной плоскостью
nmk,
содержащей касательную к кривой.
Разность
астрономического и геодезического
азимутов
некоторого направления в данной точке
равна разности астрономической и
геодезической долгот, умноженной на
синус широты этой точки Ам=м-(-L)*sin.
Астрономо-геодезическое
уклонение отвесной линии
– угол между нормалью к поверхности
эллипсоида и отвесной линией в данной
точка. Различают абсолютные и относительные
уклонения отвесных линий.1. Абсолютное
уклонение отвесной линии
– угол между нормалью к общему земному
эллипсоиду и направлением отвесной
линии в данной точке.2. Относительное
уклонение отвесной линии
– угол между нормалью к поверхности
референц-эллипсоида и отвесной линией
в данной точке.Отклонение отвесных
линий позволяет:1. изучать фигуру земли2.
переходить от астрономических координат
к геодезическим координатам3. переходить
от астрономических азимутов к
геодезическим4. переходить от результатов
измерений на физической поверхности
эллипсоида к их проекциям на поверхность
эллипсоида вращения.
Существует
3 наземных способа определения отклонений
отвесных линий:1.
астрономо-геодезический.Создаётся
государственная геодезическая сеть,
на пунктах которой выполняют астрономические
определения координат пунктов. 2.
гравиметрический способ.Уклонения
отвесных линий и аномалии силы тяжести
– это следствие несовпадения
действительного и нормального потенциалов
силы тяжести Земли. Если выполнить
гравиметрическую съёмку, то можно
определить эти абсолютные уклонения.3.
астрономо-гравиметрический способ.
В области
G
выполняется гравиметрическая съёмка
на всех пунктах (А, В, С, D,
К). Внутри области G
выберем такую область G0
, чтобы в ней влияние неучтённых зон на
разность между уклонениями отвесных
линий, вычисленных по астрономо-геодезическому
и гравиметрическому способам, носило
линейный характер. При этом в пунктах
А, В, С, D
были произведены астрономо-геодезические
наблюдения по определению отклонения
отвесных линий. Далее численным
интерполированием находим относительное
отклонение отвеса в точке К. Этот способ
позволяет получить отклонение отвеса
с ошибкой 0,8'' при расстояниях между
астропунктами до 200 км. Явление уклонения
отвеса наблюдается повсеместно. В
равнинных областях величины уклонения
отвеса составляют, как правило, несколько
секунд. Обычно
уклонения отвеса определяются его
проекциями на плоскость меридиана и
первого вертикала. Они
вычисляются в пунктах Лапласа или в
промежуточных астрономических пунктах
государственной сети триангуляции 1
класса, в которых определяются
астрономические координаты
и
строномические
координаты.Положение
точки на поверхности сферы определяется
двумя сферическими координатами –
широтой и долготой (О-центр сферы; точка
Р-северный полюс; точка Р’-южный полюс).
Проведём линию экватора QQ’
полученную от пересечения плоскости
экватора и поверхности сферы.
Широта
φ точки А – это
угол,
образованный
отвесной линией точки А и плоскостью
экватора;
этот угол лежит в плоскости меридиана
точки. Широта
отсчитывается в обе стороны от экватора
(к северу – северная широта, к югу –
южная) и изменяется от 00
до 900.Долгота
точки λ - это
двугранный угол между плоскостью
начального меридиана и плоскостью
астрономического меридиана точки А.
Начальный меридиан проходит через центр
главного зала Гринвичской обсерватории,
расположенной вблизи Лондона. Плоскость
астрономического меридиана – плоскость,
проходящая через отвесную линию в данной
точки и распологающуюся параллельно
оси вращения земли. Долготы изменяются
от 00 до
1800,
к западу от Гринвича – западные и к
востоку – восточные. Все точки одного
меридиана имеют одинаковую долготу.
Проведём плоскость G,
касательную к поверхности сферы в точке
А;
эта плоскость называется плоскостью
горизонта точки А.
Линия пересечения плоскости горизонта
и плоскости меридиана точки называется
полуденной
линией ;
направление полуденной линии – с юга
на север. Если провести полуденные линии
двух точек, лежащих на одной параллели,
то они пересекутся в точке на продолжении
оси вращения Земли PP’
и образуют угол ,
который называется сближением меридианов
этих точек. Широту
и долготу точек местности определяют
из астрономических наблюдений, потому
они и называются астрономическими
координатами. Астрономические наблюдения
в общем случае заключаются в
измерении:1,зенитных расстояний светил,2,
измерении соответствующих горизонтальных
углов,3,фиксации моментов времени этих
измерений по часам.Геодезические
координаты.
На поверхности эллипсоида вращения
положение точки определяется геодезическими
координатами – геодезической широтой
В,
геодезической долготой L
и геодезической высотой НГ.
Геодезическая
широта В точки М –
это угол, образованный нормалью Mn
к поверхности эллипсоида в этой точке
и плоскостью экватора ЕСЕ1.
Геодезические широты отсчитываются от
плоскости экватора к северному полюсу
со знаком плюс, а к южному полюсу – со
знаком минус, от 0º до 90º
Геодезическая
долгота L
точки М– это
двугранный угол между плоскостью PEP1
начального меридиана (гринвический) и
плоскостью PmP1
меридиана данной точки M.
Плоскость
геодезического меридиана проходит
через точку M
и малую полуось эллипсоида; в этой
плоскости лежит нормаль к поверхности
эллипсоида в точке M.
Геодезическая параллель получается от
пересечения поверхности эллипсоида
плоскостью, проходящей через точку M
и параллельной плоскости экватора.
Различие
геодезических и астрономических
координат
точки M
зависит от угла между отвесной линией
данной точки и нормалью к поверхности
эллипсоида в этой же точке. Этот угол
называется уклонением отвесной линии;
он обычно не превышает 5”. В некоторых
районах Земли, называемых аномальными,
уклонение отвесной линии достигает
нескольких десятков дуговых секунд.
При геодезических работах невысокой
точности астрономические и геодезические
координаты не различают; их общее
название – географические координаты
– используется довольно часто. Широта:
северная или южная 0≤B≤90º.
Долгота:
западная или восточная 0≤L≤180º
. Через
уклонение отвесных линий устанавливается
простая связь между астрономическими
и геодезическими координатами. Это
позволяет, зная уклонения отвесных
линий, переходить от астрономических
координат
и
к геодезическим В и L
при помощи формул: В=+,
L=+
}, где
и
- весьма простые функции слагающих
уклонений отвесных линий в меридиане
и первом вертикале. Это соотношение
имеет и другое принципиальное значение:
если оба слагаемых правой части вывести
из измерений, то тем самым можно определить
две координаты точек поверхности Земли,
изучение которой составляет главную
задачу высшей геодезии. Возможность
перехода координат крайне важна, в
частности при использовании астрономических
пунктов как опорных, при топографических
съёмках.Астрономический
азимут αмk
– называется угол между плоскостью
астрономического меридиана в данной
точке М и вертикальной плоскостью,
проходящей через точку k.
Геодезический
азимут Амk
– двугранный угол Pmk
в точке m,
образованный плоскостью геодезического
меридиана PmP1
данной точки и нормальной плоскостью
nmk,
содержащей касательную к кривой.
Разность
астрономического и геодезического
азимутов
некоторого направления в данной точке
равна разности астрономической и
геодезической долгот, умноженной на
синус широты этой точки Ам=м-(-L)*sin.
Астрономо-геодезическое
уклонение отвесной линии
– угол между нормалью к поверхности
эллипсоида и отвесной линией в данной
точка. Различают абсолютные и относительные
уклонения отвесных линий.1. Абсолютное
уклонение отвесной линии
– угол между нормалью к общему земному
эллипсоиду и направлением отвесной
линии в данной точке.2. Относительное
уклонение отвесной линии
– угол между нормалью к поверхности
референц-эллипсоида и отвесной линией
в данной точке.Отклонение отвесных
линий позволяет:1. изучать фигуру земли2.
переходить от астрономических координат
к геодезическим координатам3. переходить
от астрономических азимутов к
геодезическим4. переходить от результатов
измерений на физической поверхности
эллипсоида к их проекциям на поверхность
эллипсоида вращения.
Существует
3 наземных способа определения отклонений
отвесных линий:1.
астрономо-геодезический.Создаётся
государственная геодезическая сеть,
на пунктах которой выполняют астрономические
определения координат пунктов. 2.
гравиметрический способ.Уклонения
отвесных линий и аномалии силы тяжести
– это следствие несовпадения
действительного и нормального потенциалов
силы тяжести Земли. Если выполнить
гравиметрическую съёмку, то можно
определить эти абсолютные уклонения.3.
астрономо-гравиметрический способ.
В области
G
выполняется гравиметрическая съёмка
на всех пунктах (А, В, С, D,
К). Внутри области G
выберем такую область G0
, чтобы в ней влияние неучтённых зон на
разность между уклонениями отвесных
линий, вычисленных по астрономо-геодезическому
и гравиметрическому способам, носило
линейный характер. При этом в пунктах
А, В, С, D
были произведены астрономо-геодезические
наблюдения по определению отклонения
отвесных линий. Далее численным
интерполированием находим относительное
отклонение отвеса в точке К. Этот способ
позволяет получить отклонение отвеса
с ошибкой 0,8'' при расстояниях между
астропунктами до 200 км. Явление уклонения
отвеса наблюдается повсеместно. В
равнинных областях величины уклонения
отвеса составляют, как правило, несколько
секунд. Обычно
уклонения отвеса определяются его
проекциями на плоскость меридиана и
первого вертикала. Они
вычисляются в пунктах Лапласа или в
промежуточных астрономических пунктах
государственной сети триангуляции 1
класса, в которых определяются
астрономические координаты
и
