6.4 Линейные или нелинейные?

Часто методы теории нелинейных систем создаются путем аналогий с линейной теорией или сведением нелинейной задачи к линейной.

Построение нелинейной теории на «линейном» фундаменте порождается представлением о линейной системе как о простейшем классе систем, а о гармоническом сигнале как о простейшем виде сигналов.

Например, подход теории абсолютной устойчивости, развиваемый с середины ХХ века, основан на рассмотрении систем, разделенных на линейную и нелинейную части (такие модели часто называют системами Лурье, см. рис. 6.4), и выведении свойств полной системы из свойств частотной характеристики линейной части (ее реакции на гармонический сигнал) и свойств множества, где лежит график нелинейности. На таком подходе основаны и современные частотные методы нелинейного анализа. Аналогично в задачах синтеза приобрел популярность метод линеаризации обратной связью (“feedback linearization”), основанный на преобразовании модели нелинейной системы к линейной форме при помощи нелинейных замен координат и обратных связей с последующим применением хорошо разработанных методов синтеза линейных систем.

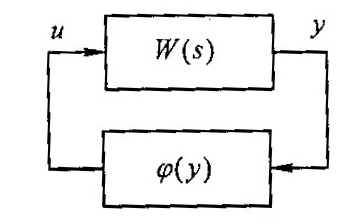
Рисунок 6.4 – Система Лурье

В 80-е годы возникла новая идея: не опираться на анализ частотных свойств линейной части модели, а развивать «частотную философию» для исходной нелинейной системы. Однако и этот подход имеет границы применимости: если на величину управляющих сигналов или на функции обратной связи наложены ограничения, то «частотная философия» и линеаризация теряют свою силу. Аналогично в присутствии нерегулярных колебаний гармонические сигналы перестают играть роль простейших сигналов а, применение частотных методов как средства анализа существенно усложняется.

Прежде всего необходимо найти адекватную замену частотной характеристике. Чтобы сделать это, сначала вернемся к классической задаче Лурье об абсолютной устойчивости системы, состоящей из линейной части, описываемой передаточной функцией

, (6.14)

и статической нелинейности

, (6.15)

график которой лежит в симметричном секторе

(6.16)

Неравенство (6.16) означает, что коэффициент усиления нелинейного блока не превосходит . Для устойчивости (6.14) – (6.16) достаточно выполнения неравенства

, (6.17)

где

(6.18)

Таким образом‚ для анализа устойчивости представляет интерес не вся амплитудно-частотная характеристика , а только ее максимум , определяемый резонансными свойствами линейной части и достигаемый на одной из резонансных частот. Для практического определения для линейной системы на ее вход следует подать гармонический сигнал и найти ω, реализующую (начальные условия на систему следует брать нулевыми).

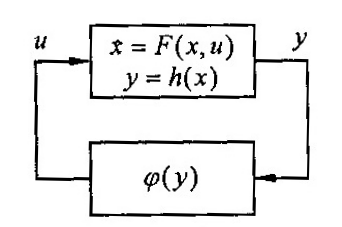
Рисунок 6.5 – Нелинейная система

Пусть теперь линейная модель системы (6.14) заменяется на нелинейную и система описывается дифференциальным уравнением состояния вместе с конечным уравнением выходов (рис. 6.5):

(6.19)

где x – n-мерный вектор состояния системы. Интуитивно ясно, что устойчивость системы (6.19), (6.15), (6.16), как и в линейном случае, должна зависеть от резонансных свойств системы (6.19). Однако изучение резонансных свойств нелинейной системы затруднено, поскольку частота вынужденных колебаний в нелинейной системе зависит от амплитуды входного гармонического сигнала. С ростом амплитуды входа в системе могут возникать сложные, в том числе хаотические режимы, т.е. входной гармонический сигнал не может в полной мере вскрыть резонансные свойства нелинейной системы.

Задачу определения формы сигнала, обеспечивающего при заданной амплитуда входа максимальную амплитуду выхода, можно поставить как задачу оптимального управления системой (6.19):

(6.20)

При этом входной сигнал, создающий максимальное возбуждение системы, будет зависеть не только от времени, но и от состояния системы, т.е. иметь вид обратной связи. Величина оптимума в задаче (6.20) зависит от γ квадратично. Поэтому естественно ввести характеристику возбудимости системы ограниченным входным сигналом как величину

(6.21)

где – оптимальное значение в задаче (6.20). Для линейных асимптотически устойчивых систем величина (6.21) не зависит от γ, а для нелинейных – представляет собой функцию от γ, которую естественно назвать степенью возбудимости системы.

Решение задачи оптимального управления в общем случае весьма трудоемко даже при использовании эффективных численных методов. Однако для приближенного решения можно воспользоваться известным результатом о возможности приближенной замены оптимального управления на локально-оптимальное, получаемое максимизацией скорости изменения целевого функционала в силу свободной системы (при ). Точность такой замены тем выше, чем меньше амплитуда входа γ.

Для вычисления локально-оптимального управления представим первую часть уравнения (6.19) в виде

(6.22)

где , , а остаточный член и имеет высший порядок малости по u. Скорость изменения целевого функционала равна

(6.23)

Пренебрегая величиной , видим, что локально-оптимальное значение входа при малых γ равно

(6.24)

Таким образом, для вычисления степени возбудимости системы при малых γ достаточно подавать на вход системы сигнал (6.24) и измерять достигаемую амплитуду выхода. Это можно делать как в физическом (натурном), так и в вычислительном эксперименте. Примеры построенных таким образом графиков степени возбудимости для классических нелинейных систем (уравнения маятника и системы Дуффинга) приведены на рис. 6.6.

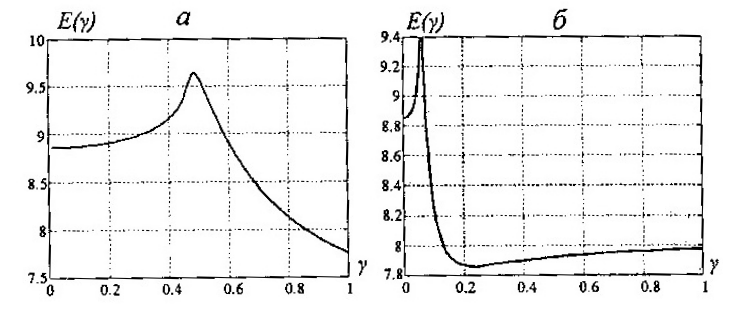
Рисунок 6.6 – Характеристики возбудимости маятника и системы Дуффинга

Полученные графики можно использовать для оценки устойчивости замкнутой системы с нелинейностью в обратной связи. Условия устойчивости аналогичны (6.17):

. (6.25)

При этом роль максимума амплитудно-частотной характеристики играет максимальная степень воэбудимости

. (6.26)

Исследование динамических свойств систем с помощью непериодических тестовых сигналов представляется весьма перспективным инструментом в теории нелинейных систем.

Другой областью, где гармонические сигналы, линейные системы и спектральные методы традиционно играли и играют ключевую роль, является теория передачи информации (теория связи). Однако и здесь «нелинейная философия» предлагает новые подходы.

Напомним‚ что в теории связи гармонический сигнал

(6.26)

рассматривается как базовый, простейший. Сигнал может изменяться (модулироваться) путем изменения его параметров – величин a (амплитуда), ω (частота) α (начальная фаза). Например, при частотной модуляции модулирующим параметром является частота ω, которая становится таким образом, переменной, т.е. с системной точки зрения становится сигналом: . Передаваемый модулированный сигнал может содержать в себе закодированное сообщение. Для передачи сообщения по каналу связи, на стороне приемника сообщение должно восстанавливаться по принимаемому сигналу , где – шум (помеха) в канале связи. Выделение полезного сообщения из принимаемого сигнала и является основной задачей теории связи.

В 90-х годах ХХ века усилился интерес к использованию в качестве несущих сигналов нерегулярных (хаотических) колебаний. Для построения соответствующей теории необходимо сделать решительный шаг: перейти от явного описания сигнала как функции времени к заданию модели системы, генерирующей этот сигнал. Очевидно, например, что генератором гармонического сигнала (6.26) может служить линейное дифференциальное уравнение

. (6.27)

Однако для генерации нерегулярных, непериодических сигналов линейные модели непригодны. Следующим шагом к построению новой теории является использование в качестве основных объектов нелинейных генераторов, описываемых дифференциальными уравнениями

(6.28)

Здесь входной вектор может иметь смысл не только входного сигнала, но и модулирующего сигнала, т.е. задавать набор изменяемых параметров генератора. Например, система (6.28) в частном случае может быть системой Лоренца или системой Чуа, а вектор входов может включать часть коэффициентов соответствующего уравнения.

Таким образом, существующие математические методы позволяют решать многие задачи анализа и синтеза нелинейных систем без опоры на «линейные костыли» – гармонические сигналы и линеаризованные модели. Это обстоятельство следует учитывать при выборе модели.

В то же время многие задачи в этой области математического моделирования не решены и даже не поставлены, что открывает широкий простор для дальнейших исследований.