2. Внешняя диффузия газа

Диффузия вещества, как известно, обусловлена различной его концентрацией в различных частях системы, и вещество перено­сится в направлении от большей концентрации к меньшей. В этом случае диффузия подчиняется двум законам Фика [уравнения (2.3)—(2.5) |. Такую диффузию часто называют молекулярной или сво­бодной диффузией. Коэффициенты свободной диффузии газоввосстановителей в бинарных смесях и длины свободного пробега молекул приведены в табл. 2.5. Коэффициент диффузии газов 1 и 2 в бинарной смеси определяется формулой

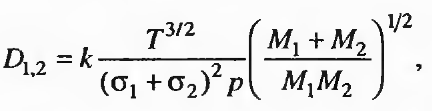(2,49)

где Т— температура, р — давление, М₁, и М₂ —молярные массы газов 1 и 2; о, и с₂— диаметры молекул газов 1 и 2, нм; к— коэффициент, за­висящий от размерности величин.

При постоянной температуре коэффициент диффузии изменяется обратно пропорционально общему давлению смеси или сумме кон­центраций компонентов смеси. Рост температуры вызывает увеличе­ние коэффициента диффузии пропорционально tв степени 3/2 (при постоянном давлении) или 1 в степени 1/2 (при постоянном количест­ве газа в единице объема). Замеры показывают, что в реальных смесях при постоянном давлении коэффициент диффузии пропорционален 1™ (где m = 1,5—2,0).

Кроме того, при движении газа, обтекающего частицы железоруд­ного материала, происходит конвективная диффузия, которая обуслов­лена разной плотностью в отдельных участках системы. Такая диффу­зия наблюдается только в подвижной среде, для нее скорость в значительной степени зависит от характера движения потока, который может быть ламинарным и турбулентным.

Таблица 2.5

Коэффициент диффузии газов D_r,см²/с (числитель) и длина свободного пробега молекул Л-10^-5, см (знаменатель), в бинарных газовых смесях (р= 98 кПа)

t,°с	co+n2	h2+n2	н2+н2о	со+со2
500	1,09/2,64	3,68/3,34	4,64/3,57	0,95/2,63
700	1,65/3,58	5,51/4,44	6,91/4,76	1,51/3,71
900	2,30/4,52	7,64/5,62	9,58/6,01	2,20/4,91
1100	3,05/5,53	10,06/6,84	12,62/7,32	3,01/6,22

При ламинарном режиме отдельные струи газа перемещаются па­раллельно твердой поверхности, и перенос диффундирующего веще­ства из среды к поверхности твердого тела и обратно (перпендикуляр­но потоку газа) осуществляется молекулярной диффузией. Турбулент­ный режим характеризуется беспорядочным движением небольших объемов газа, скорость которых непрерывно меняется по величине и направлению. Концентрация вещества в объеме в результате переме­шивания сравнительно быстро выравнивается, но у твердой поверхно­сти всегда имеется малоподвижный тонкий слой, где сохраняются ла­минарный режим и градиент концентрации газа. Этот пограничный (или диффузионный) слой создает наибольшее сопротивление перено­су газа, так как в нем протекает сравнительно медленная молекуляр­ная диффузия. Следовательно, перенос определяется переходом газа через эту пленку, а наблюдаемая скорость диффузии (или диффузион­ный поток Г) — уравнением

(2.50)

Уравнение (2.50) получают из выражения (2.3) при условии, что толщина пограничного слоя /, концентрации газа на границах погра­ничного слоя являются постоянными и равными С,, и С₂, а количест­во газа, входящего и выходящего из пограничного слоя, постоянно. В этом случае концентрация газа в пограничном слое меняется от Cj до С₂ линейно.

При оценке внешнего переноса обычно пользуются критериями подобия. Критерий Рейнольдса характеризует соотношение сил вязко­сти и инерции в движущейся среде:

(2.51)

где р — плотность среды; и — скорость среды; d— характеристический размер потока; г] — коэффициент динамической вязкости.

Критерий Пекле характеризует соотношение количества вещества, переносимого за счет конвекции (udC/dx) и диффузии D d²C/dx²\

Ре = ud/D, (2.52)

где D— коэффициент диффузии газа.

При большом значении Ре молекулярной диффузией можно пре­небречь по сравнению с конвективной. При Re«1, наоборот, прене­брегают конвективной диффузией по сравнению со свободной.

Критерий Шмидта является диффузионным критерием (аналоги­чен критерию Прандтля для теплообмена):

(2.53)

где v = 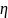/p — коэффициент кинематической вязкости.

Для газов Sc~ 1 и Ре ~ Re.

Если обозначить D/1 =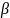 получим

(2.54)

Величину Р называют коэффициентом массопередачи. Он зависит от всех величин, определяющих скорость переноса, кроме концентра­ций, и по аналогии с коэффициентом пропорциональности в выраже­нии закона действия масс его иногда называют константой скорости диффузии. При турбулентном движении Р имеет характер эмпириче­ского коэффициента и его значение зависит от газодинамической обстановки процесса. С повышением скорости потока газа и степени его турбулентности толщина пограничного слоя газа уменьшается, а величина коэффициента массопередачи возрастает.

Связь массообмена с газодинамикой потока может быть выражена эмпирической функцией

l/d=ARe,Sc). (2.55)

При сопоставлении этой величины с формулой коэффициента массообмена можно получить критерий Шервуда (аналогичный крите­рию Нуссельта для теплообмена):

Sh= р d/D. (2.56)

В этих выражениях d— характеристическое расстояние, обознача­ющее размер обтекаемого газом сферического куска. Критерий Шер­вуда связан с критериями Рейнольдса и Шмидта следующим образом:

Sh = C + CRe^mScⁿ, (2.57)

где С и С— константы.

Для случая, когда газ обтекает шарообразные куски, С = 2, при и = 0 величина Sh=2, С = 0,6. Для ламинарного потока т = 1/2, п = 1/3. Для турбулентного потока т = 0,5—0,8; п = 1/3. Отсюда коэффициент массопередачи приблизительно пропорционален квадратно­му корню из скорости газа.

Критерий Шмидта для чистых газов в зависимости от давления, температуры и типа газа составляет 0,6—0,8. Для газовых смесей кри­терий Шмидта, чаще всего, имеет меньшее значение, чем для чистых газов. Для смеси водорода и диоксида углерода (соотношение 1:1) Sc = 0,25 при 20 °С. С ростом доли более тяжелого компонента вели­чина критерия Шмидта снижается, так как в интервале 50—100% С0₂ вязкость почти постоянна, плотность растет, a D₁₂ остается почти по­стоянным. Для смесей Н₂ = N₂также характерно подобное явление.

До последнего времени шли споры о возможности лимитирующего влияния внешней диффузии на общую скорость восстановления желе­зорудных материалов. Рассмотрим некоторые простые соотношения. Считаем, что процесс состоит из двух стадий: химической реакции и внешней диффузии.

Для описания совместного протекания химической реакции на по­верхности и диффузии применяют различные приближенные методы. В одном из них методе равнодоступной поверхности, разработанном Д.А. Франк-Каменецким, принимается, что все участки реакционной поверхности одинаково доступны для диффузии; диффузия и химиче­ская реакция протекают последовательно и независимо друг от друга; концентрация газа-восстановителя одинакова на всей поверхности. Это возможно при отсутствии глубоких и мелких пор в реагирующем твердом теле. Вся реакционная поверхность может рассматриваться как внешняя.

Для простых химических реакций изменение скорости

( 2.58)

где с — концентрация газа-восстановителя на поверхности оксида; к — константа скорости реакции; и — порядок реакции.

Для процесса на единице наружной поверхности беспористого ма­териала, когда п = 1, можно записать

(2.59)

где С₀ — концентрация газа-восстановителя в ядре потока.

Равенство скоростей последовательных звеньев (диффузии и реак­ции) и наблюдаемой скорости процесса при установившемся режиме обосновано, например, H.JI. Гольдштейном, тогда

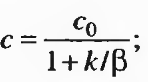(2.60)

(2.61)

Таким образом, наблюдаемая константа скорости процесса из урав­нения (2.61)

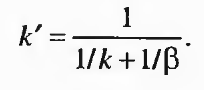
(2.62)

Ее удобнее выразить через обратные величины, т.е.

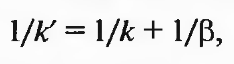(2.63)

где первое слагаемое характеризует химическое, а второе — внешне­диффузионное звено процесса.

Из уравнения (2.63) следует, что обратная величина наблюдаемой константы скорости процесса восстановления равна сумме обратных значений констант скоростей последовательных звеньев процесса. Та­кой вывод, полученный для реакции, состоящей из двух стадий, при­меним в простейшем случае (если все звенья имеют первый порядок) к системам с любым числом последовательных звеньев.

Если константа скорости характеризует пропускную способность того или иного звена, то обратное ее значение представляет собой со­противление этого звена. Следовательно, уравнение (2.63) показывает, что общее сопротивление протеканию процесса равно сумме сопроти­влений последовательных звеньев. Необходимо отметить, что это явление аналогично законам построения электрических цепей.

При фильтрации газа через слой частиц или обтекании отдельных кусков по формуле Сокольского

(2.64)

повышение линейной скорости газа приводит к увеличению наблюда­емой константы скорости процесса, которая стремится к постоянному значению, когда внешнедиффузионное сопротивление становится пренебрежимо малым по сравнению с химическим сопро­тивлением.

Однако эти представления, хотя и широко распространены в лите­ратуре, не подтверждаются наблюдаемой количественной связью ско­рости процесса с расходом газа, которая показывает, что при малых расходах газа скорость процесса возрастает в гораздо большей мере, чем это следует из указанной формулы. Наряду с этими данными (H.JI. Гольдштейна, К.К. Шкодина и др.) результаты опытов Ю.П. Свинцова, К.К. Шкодина показали, что при изменении линей­ной скорости газа в случае постоянного его расхода скорость процесса вообще не меняется.

Таким образом, при реальных условиях процесса восстановления и фильтрации газом слоя кусковых железорудных материалов внешняя диффузия не может лимитировать процесс восстановления, а влияние массового расхода газа на скорость процесса следует объяснять иными факторами, что будет рассмотрено ниже.

Между прочим, отсутствие тормозящего влияния внешней диффу­зии можно проиллюстрировать другими рассуждениями.

Если иметь в виду, что критерий Нусселъта

(2.65)

где а — коэффициент теплопередачи, Дж/(см² с-К); А, — коэффициент теплопроводности, ДжДсм с К); d—характеристическая величина раз­мера твердого тела, см, а критерий Прандтля

(2.66)

где v — кинематическая вязкость газа, см²/с; а — температуропровод­ность, см²/ с, то можно пересчитать критерий Нуссельта в критерий Шервуда, используя зависимости этих критериев от Re,и соответст­венно определить значение коэффициентов массообмена Р и теплопе­редачи а.

Поскольку константа С в уравнениях

(2.67)

должна иметь для равных геометрических соотношений одинаковое численное значение, получаем

. (2.68)

По данным И.С. Куликова и др.,

(2.69)

Откуда

(2.70)

Следовательно, Если то Темпера­турная зависимость других звеньев процесса значительно сильнее. Именно поэтому сколько-нибудь заметное влияние внешнего массопереноса на общую скорость восстановления может проявиться при очень высоких температурах.