Образец оформления титульного листа контрольной работы
ГБОУ ВПО
«Набережночелнинский государственный торгово-технологический институт»
КОНТРОЛЬНАЯ РАБОТА
по дисциплине “Статистика”
Выполнил: студент группы 395-з
Иванов И.И.
зачетная книжка № 031456
Проверил: д.ф.-м.н., профессор
Исавнин А.Г.
Набережные Челны
2011
Пример выполнения контрольной работы № 2.
Курс акций компании “ЛОТОС” в марте 2011 года составлял (в тыс. руб.):
-
Дата
1
2
3
4
5
6
7
8
9
10
Курс
5
5
7
6
7
8
9
8
11
12
Дата
11
12
13
14
15
16
17
18
19
20
Курс
11
14
15
16
17
16
18
20
20
23
ti – моменты времени (числа месяца), yi – уровни динамического рядя (курс акций, тыс.руб.).
Сглаживание динамического ряда методом простой скользящей средней, периоды скольжения – 3 и 5 (например, 5.67=(5+5+7)/3, 6=(5+7+6)/3 и т.д.) :
Ti |
Yi |
yi_(3) |
yi_(5) |
1 |
5 |
|
|
2 |
5 |
5,67 |
|
3 |
7 |
6 |
6 |
4 |
6 |
6,67 |
6,6 |
5 |
7 |
7 |
7,4 |
6 |
8 |
8 |
7,6 |
7 |
9 |
8,33 |
8,6 |
8 |
8 |
9,33 |
9,6 |
9 |
11 |
10,3 |
10,2 |
10 |
12 |
11,3 |
11,2 |
11 |
11 |
12,3 |
12,6 |
1 |
14 |
13,3 |
13,6 |
13 |
15 |
15 |
14,6 |
14 |
16 |
16 |
15,6 |
15 |
17 |
16,3 |
16,4 |
16 |
16 |
17 |
17,4 |
17 |
18 |
18 |
18,2 |
18 |
20 |
19,3 |
19,4 |
19 |
20 |
21 |
|
20 |
23 |
|
|
210 |
248 |
|
|
2
Аналитические показатели динамики.
Прб – абсолютный прирост базисный (y0=5) (Прб = yi-y0).
Прц - абсолютный прирост цепной (Прц = yi-yi-1).
Трб – темп роста базисный (%) (Трб = yi/y0*100%).
Трц – темп роста цепной (%) (Трц = yi/yi-1*100%).
Тпрб - темп прироста базисный (%) (Тпрб = Прб/y0*100%).
Тпрц - темп прироста цепной (%) (Тпрц = Прц/yi-1*100%).
Абс_уск – абсолютное ускорение (Абс_уск = Прцi –Прцi-1)
ti |
yi |
Прб |
Прц |
Трб |
Трц |
Тпрб |
Тпрц |
Абс_уск |
1 |
5 |
0 |
|
100 |
|
0 |
|
|
2 |
5 |
0 |
0 |
100 |
100 |
0 |
0 |
|
3 |
7 |
2 |
2 |
140 |
140 |
40 |
40 |
2 |
4 |
6 |
1 |
-1 |
120 |
85,71 |
20 |
-14,29 |
-3 |
5 |
7 |
2 |
1 |
140 |
116,67 |
40 |
16,67 |
2 |
6 |
8 |
3 |
1 |
160 |
114,29 |
60 |
14,29 |
0 |
7 |
9 |
4 |
1 |
180 |
112,5 |
80 |
12,5 |
0 |
8 |
8 |
3 |
-1 |
160 |
88,89 |
60 |
-11,11 |
-2 |
9 |
11 |
6 |
3 |
220 |
137,5 |
120 |
37,5 |
4 |
10 |
12 |
7 |
1 |
240 |
109,09 |
140 |
9,09 |
-2 |
11 |
11 |
6 |
-1 |
220 |
91,67 |
120 |
-8,33 |
-2 |
12 |
14 |
9 |
3 |
280 |
127,27 |
180 |
27,27 |
4 |
13 |
15 |
10 |
1 |
300 |
107,14 |
200 |
7,14 |
-2 |
14 |
16 |
11 |
1 |
320 |
106,67 |
220 |
6,67 |
0 |
15 |
17 |
12 |
1 |
340 |
106,25 |
240 |
6,25 |
0 |
16 |
16 |
11 |
-1 |
320 |
94,12 |
220 |
-5,88 |
-2 |
17 |
18 |
13 |
2 |
360 |
112,5 |
260 |
12,5 |
3 |
18 |
20 |
15 |
2 |
400 |
111,11 |
300 |
11,11 |
0 |
19 |
20 |
15 |
0 |
400 |
100 |
300 |
0 |
-2 |
20 |
23 |
18 |
3 |
460 |
115 |
360 |
15 |
3 |
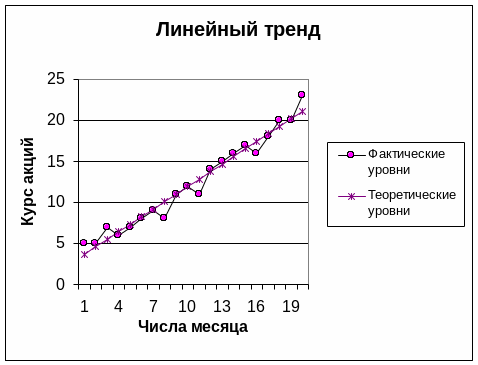
Линейный тренд yi = ati+b, yi~ - теоретические (выравненные) уровни, получаемые подстановкой значений ti в уравнение тренда. В последней строке представлены суммы значений столбцов.
ti |
yi |
ti^2 |
ti*yi |
yi~ |
(yi-yi~)^2 |
1 |
5 |
1 |
5 |
3,686 |
1,72735 |
2 |
5 |
4 |
10 |
4,603 |
0,1576 |
3 |
7 |
9 |
21 |
5,52 |
2,18951 |
4 |
6 |
16 |
24 |
6,438 |
0,19149 |
5 |
7 |
25 |
35 |
7,355 |
0,12594 |
6 |
8 |
36 |
48 |
8,272 |
0,07408 |
7 |
9 |
49 |
63 |
9,189 |
0,0359 |
8 |
8 |
64 |
64 |
10,11 |
4,43847 |
9 |
11 |
81 |
99 |
11,02 |
0,00058 |
10 |
12 |
100 |
120 |
11,94 |
0,00344 |
11 |
11 |
121 |
121 |
12,86 |
3,45457 |
12 |
14 |
144 |
168 |
13,78 |
0,0502 |
13 |
15 |
169 |
195 |
14,69 |
0,09411 |
14 |
16 |
196 |
224 |
15,61 |
0,15169 |
15 |
17 |
225 |
255 |
16,53 |
0,22295 |
16 |
16 |
256 |
256 |
17,45 |
2,08835 |
17 |
18 |
289 |
306 |
18,36 |
0,13134 |
18 |
20 |
324 |
360 |
19,28 |
0,51883 |
19 |
20 |
361 |
380 |
20,2 |
0,03881 |
20 |
23 |
400 |
460 |
21,11 |
3,55592 |
210 |
248 |
2870 |
3214 |
248 |
19,2511 |
Метод наименьших квадратов дает следующие формулы для нахождения параметров линейного тренда:
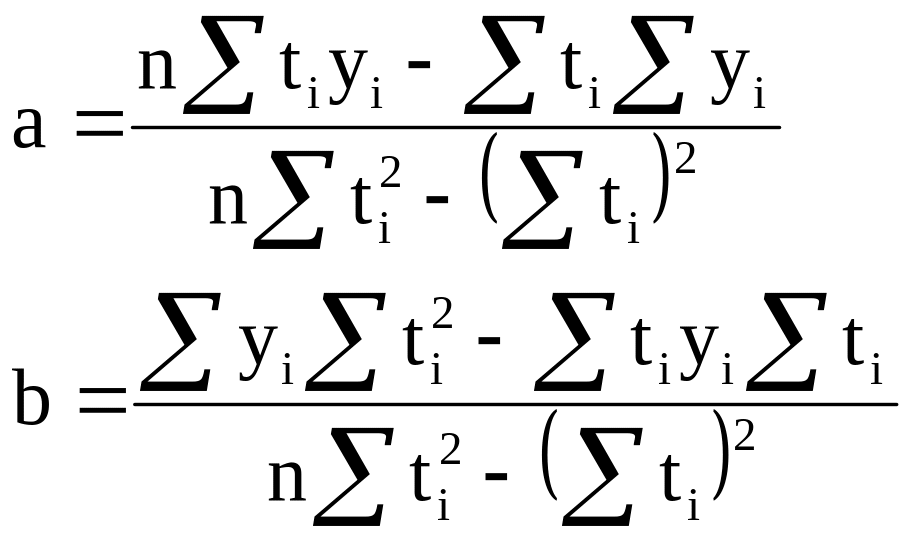
a=0,917; b=2,768. Линейный тренд: y=0.917t+2.768.
Точность трендовой модели можно оценить с помощью стандартизованной ошибки аппроксимации (СОА):
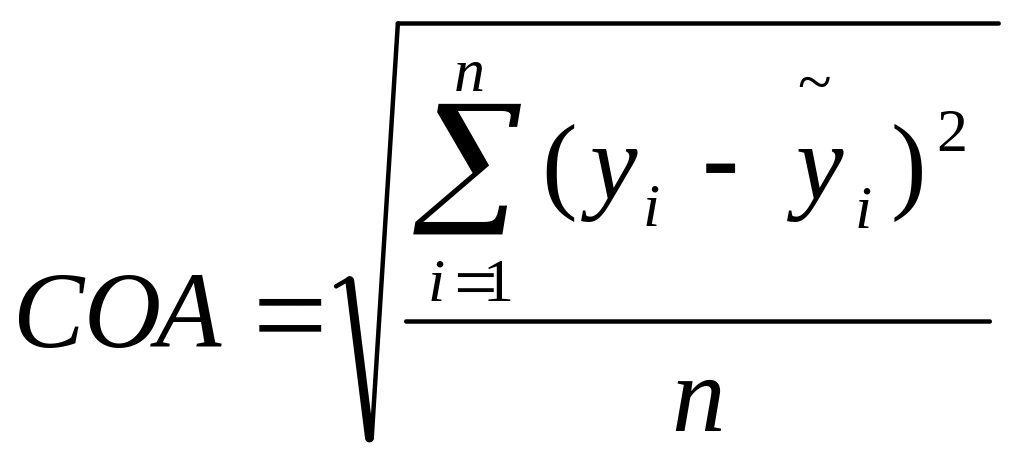
СОА=0.981
Некоторые нелинейные функции с помощью соответствующих замен переменных могут быть преобразованы к линейному виду.
Показательный тренд y=bat . В результате логарифмирования получим:
Lny = tlna+lnb или Y=At+B (получили линейный вид), где Y=lny, A=lna, B=lnB.
ti |
yi |
Yi=ln(yi) |
ti^2 |
ti*Yi |
yi~ |
(yi-yi~)^2 |
1 |
5 |
1,60944 |
1 |
1,609 |
5,233 |
0,05431 |
2 |
5 |
1,60944 |
4 |
3,219 |
5,668 |
0,44669 |
3 |
7 |
1,94591 |
9 |
5,838 |
6,14 |
0,73981 |
4 |
6 |
1,79176 |
16 |
7,167 |
6,651 |
0,42332 |
5 |
7 |
1,94591 |
25 |
9,73 |
7,204 |
0,04156 |
6 |
8 |
2,07944 |
36 |
12,48 |
7,803 |
0,03876 |
7 |
9 |
2,19722 |
49 |
15,38 |
8,452 |
0,30004 |
8 |
8 |
2,07944 |
64 |
16,64 |
9,155 |
1,33482 |
9 |
11 |
2,3979 |
81 |
21,58 |
9,917 |
1,17302 |
1 |
12 |
2,48491 |
100 |
24,85 |
10,74 |
1,58284 |
11 |
11 |
2,3979 |
121 |
26,38 |
11,64 |
0,40382 |
12 |
14 |
2,63906 |
144 |
31,67 |
12,6 |
1,95057 |
13 |
15 |
2,70805 |
169 |
35,2 |
13,65 |
1,81765 |
14 |
16 |
2,77259 |
196 |
38,82 |
14,79 |
1,47032 |
15 |
17 |
2,83321 |
225 |
42,5 |
16,02 |
0,96523 |
16 |
16 |
2,77259 |
256 |
44,36 |
17,35 |
1,82243 |
17 |
18 |
2,89037 |
289 |
49,14 |
18,79 |
0,62924 |
18 |
20 |
2,99573 |
324 |
53,92 |
20,36 |
0,12715 |
19 |
20 |
2,99573 |
361 |
56,92 |
22,05 |
4,20235 |
20 |
23 |
3,13549 |
400 |
62,71 |
23,88 |
0,78183 |
210 |
248 |
48,2821 |
2870 |
560,1 |
248,1 |
20,3058 |
0
А и В найдем по соответствующим формулам для линейного тренда.
А=0.0799, И=1.5751. a=exp(A)=1.083, b=exp(B)=4.841, т.е. показательный тренд имеет вид: y = 4.841*1.083t. СОА=1.008.
Гиперболический тренд y=a/t+b или y=aT+b, где T=1/t.
ti |
yi |
Ti |
Ti^2 |
Ti*yi |
yi~ |
(yi-yi~)^2 |
1 |
5 |
1 |
1 |
5 |
-0,449 |
29,693 |
2 |
5 |
0,5 |
0,25 |
2,5 |
7,3846 |
5,68645 |
3 |
7 |
0,3333 |
0,111 |
2,3333 |
9,9959 |
8,97529 |
4 |
6 |
0,25 |
0,063 |
1,5 |
11,302 |
28,1059 |
5 |
7 |
0,2 |
0,04 |
1,4 |
12,085 |
25,856 |
6 |
8 |
0,1667 |
0,028 |
1,3333 |
12,607 |
21,2256 |
7 |
9 |
0,1429 |
0,02 |
1,2857 |
12,98 |
15,8417 |
8 |
8 |
0,125 |
0,016 |
1 |
13,26 |
27,667 |
9 |
11 |
0,1111 |
0,012 |
1,2222 |
13,478 |
6,13824 |
10 |
12 |
0,1 |
0,01 |
1,2 |
13,652 |
2,72788 |
11 |
11 |
0,0909 |
0,008 |
1 |
13,794 |
7,80678 |
12 |
14 |
0,0833 |
0,007 |
1,1667 |
13,913 |
0,00761 |
13 |
15 |
0,0769 |
0,006 |
1,1538 |
14,013 |
0,9738 |
14 |
16 |
0,0714 |
0,005 |
1,1429 |
14,099 |
3,61276 |
15 |
17 |
0,0667 |
0,004 |
1,1333 |
14,174 |
7,98695 |
16 |
16 |
0,0625 |
0,004 |
1 |
14,239 |
3,10055 |
17 |
18 |
0,0588 |
0,003 |
1,0588 |
14,297 |
13,714 |
18 |
20 |
0,0556 |
0,003 |
1,1111 |
14,348 |
31,9455 |
19 |
20 |
0,0526 |
0,003 |
1,0526 |
14,394 |
31,4298 |
20 |
23 |
0,05 |
0,003 |
1,15 |
14,435 |
73,3591 |
210 |
248 |
3,5977 |
1,596 |
29,744 |
248 |
345,854 |
a=-15.667, b=15.218, т.е. гиперболический тренд записывается в следующей форме:
y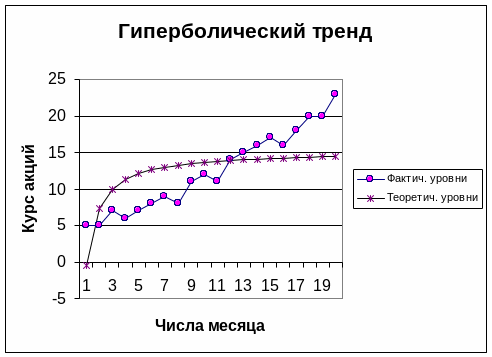
=-15.667/t+15.218.
СОА=4.158.
Лучшим, т.е. имеющим наименьшую СОА, оказался линейный тренд.
Точечный прогноз на 21 марта 2011 года получим, подставив t=21 в уравнение лучшего (линейного) тренда. y(21) = 0.917*21+2.768 = 22.025.
Число степеней свободы k=n-m, где n – число уровней динамического ряда, m - число параметров в лучшей трендовой модели. В нашем случае k=20-2=18. Из таблиц возьмем значение t-критерия Стьюдента для уровней значимости =0.1 и 0.05:
t(0.1, 18)=1.73,
t(0.05, 18)=2.1.
Границы доверительного интервала можно определить как y(21)t(, k)S, где
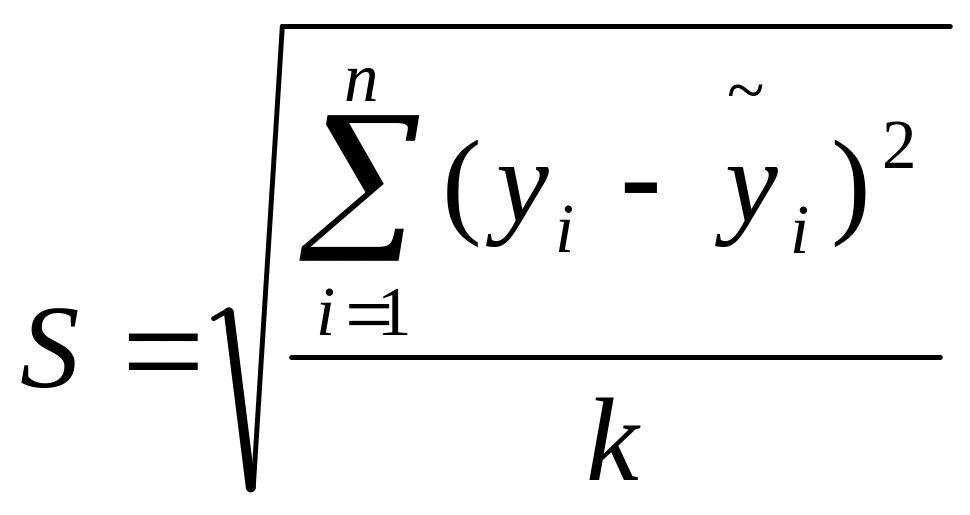
Таким образом, с доверительной вероятностью 0.9 (равной 1-) можно утверждать, что стоимость акции 21 марта окажется в пределах от 20.235 до 23.814 . При доверительной вероятности 0.95 границы доверительного интервала окажутся от 19.854 до 24.196 (тыс.руб.).