1.8 Среднеквадратичное приближение функций.

1.8.1. Общая постановка задачи и ее разрешимость.

Пусть задана система функций , - весовая функция.

Определение. Обобщенным полиномом порядка по системе называется линейная комбинация

где – произвольные вещественные коэффициенты.

Постановка задачи среднеквадратичного приближения функции .

Найти такой обобщенный полином

наименее уклоняющийся от функции в метрике , т.е. удовлетворяющий условию:

.

Многочлен , удовлетворяющий указанному условию, называется многочленом наилучшего среднеквадратичного приближения.

Теорема 1.4. Если система функций линейно независима, то задача среднеквадратичного приближения однозначно разрешима.

Распишем квадрат расстояния между функцией и полиномом:

.	(29)

Очевидно, что величина - неотрицательно определенная квадратичная функция переменных , а такая функция всегда имеет минимум. Т.о. решение задачи среднеквадратичного приближения существует.

Докажем единственность решения. Минимум функции можно найти из необходимых условий экстремума (для неотрицательной квадратичной функции они являются так же и достаточными):

Применяя данное условие к (29), получим систему линейных уравнений:

(30)

Система (30) называется нормальной системой уравнений.

Выпишем определитель системы (30).

(31)

Определитель (31) – так называемый определитель Грама системы функций .

В курсе линейной алгебры доказывается, что, если система линейно независима, то , отсюда следует существование и единственность решения (30).

Доказывается от противного. Пусть однородная система уравнений, получаемая из (2) при нулевой правой части имеет нетривиальное решение. Обозначим его .

Используя свойства скалярного произведения, запишем уравнения однородной системы следующим образом:

(32)

Умножая уравнения системы (32) соответственно на и складывая, получим

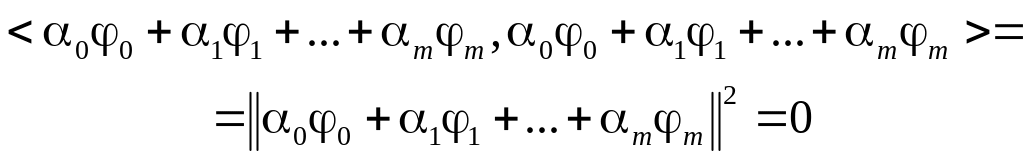
Отсюда по свойству нормы следует, что ,

причем не все тождественно равны нулю, а это значит, что система - линейно зависима, что противоречит условию теоремы. Т.о. и неоднородная система (30) имеет единственное решение.

Наиболее просто решается система (30), если система функций - ортогональна, т.е. выполняется условие .

Заметим, что справедливо одно из важных свойств ортогональной системы функций: если система - ортогональна, то она линейно независима.

Пусть система ортогональна на . Тогда система (30) становится диагональной:

.

Отсюда искомые коэффициенты находим по формуле

.

(33)

и тем самым определяется многочлен наилучшего среднеквадратичного приближения:

.

Полученный обобщенный многочлен называют обобщенным многочленом Фурье для функции по системе , а коэффициенты - коэффициентами Фурье.

1.8.2. Среднеквадратичное приближение функций алгебраическими многочленами.

Рассмотрим систему алгебраических многочленов

.

(34)

Такая система, рассматриваемая в гильбертовом пространстве , линейно независима при .

Однако непосредственная подстановка алгебраических многочленов в систему (30) не эффективна, т.к. приводит к плохо обусловленной системе уравнений. На базе системы (34) можно построить ортогональные полиномы на заданном отрезке (или бесконечном промежутке) с заданной весовой функцией .

Рассмотрим один из алгоритмов ортогонализации, известный как рекуррентная процедура Грама-Шмидта.

Новая система полиномов, ортогональная на с весом строится рекуррентно:

.

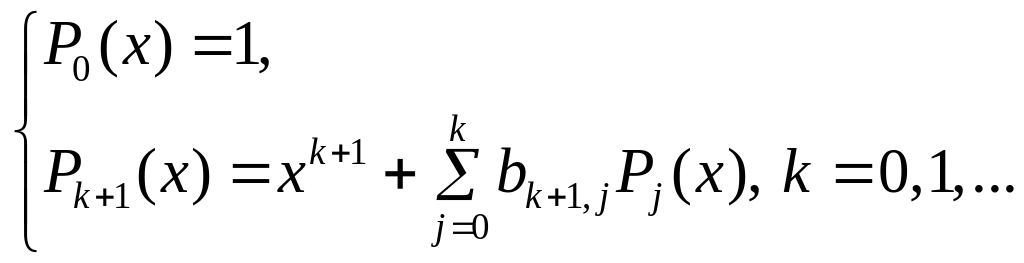Накладывая условие ортогональности:

,

получаем формулу для коэффициентов :

(35)

Пример 16. Пусть отрезок . Построить первые три ортогональных полинома , используя процедуру Грама-Шмидта.

Полагаем . Далее по формулам (35) находим

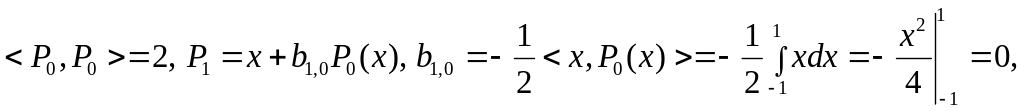
откуда получаем

Действуя аналогично далее, получаем: .

Существует другой - более эффективный способ построения ортогональных многочленов. В частности, для системы ортогональных многочленов на отрезке с весом , справедливы следующие две формулы:

формула Родрига:

(36)

и

рекуррентная формула:

(37)

Из (36) последовательно получаем: ; Далее по рекуррентной формуле (37) при находим: .

Получаемые таким образом полиномы называются полиномами Лежандра.

Замечание. Найденные по процедуре (36)-(37) ортогональные многочлены могут лишь множителями отличаться от тех, которые строятся по методу Грама-Шмидта.

Квадрат нормы полиномов Лежандра равен