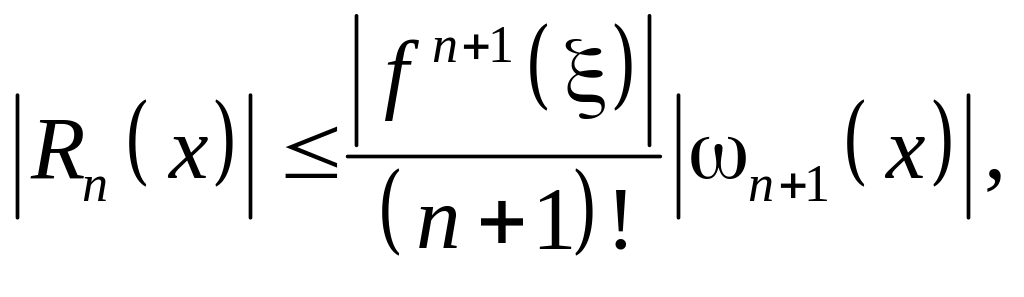1.5 Конечные разности и их свойства.

Пусть задана равномерная сетка узлов . Обозначим – множество узловых точек; - шаг сетки.

Определение. Величина

называется конечной разностью первого порядка (или разностью «на шаг вперед»).

……………………..

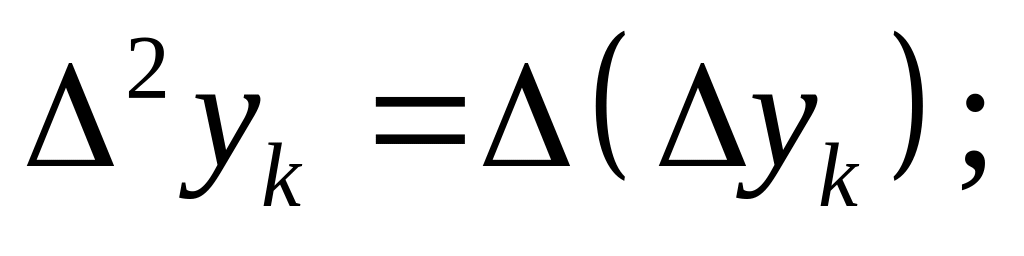
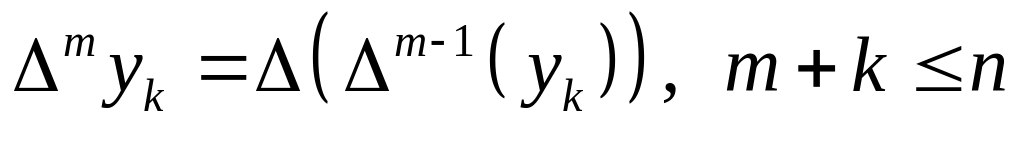
(13)

- конечная разность m-го порядка.

Свойства конечных разностей.

1. Операторы - линейные операторы.

Пусть - произвольные табличные значения.

Доказательство проведем по индукции. Вначале проверяем утверждение для m=1.

оператор линейный.

Далее пусть - линейный оператор. Покажем, что и линейный.

2. Операторы и - перестановочные, т.е.

.

Последовательно используя определение (13), получаем следующую цепочку равенств:

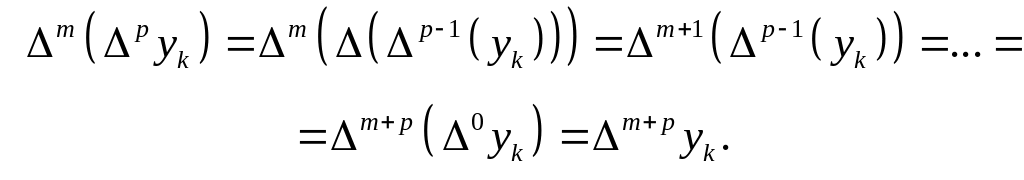
То же самое получим, действуя в обратном порядке.

Следствия из свойств 1 и 2.

С.1.

С.2. линейно выражается через узловые значения .

По индукции. Для m=1 утверждение следует из определения оператора . Пусть утверждение справедливо для оператора , т.е. , где m>2, тогда

Пример 9. Выразить явно через .

Самостоятельно.

3. Рассмотрим сетку , в которую введен дополнительный узел . Пусть функция Тогда справедливы следующие формулы:

.	(14)
.	(15)

Пусть m=1. Тогда

где h – приращение аргумента.

m=2.

(14) при .

Уравнение (15) является частным случаем уравнения (14) при .

4. Для сетки X_n рассмотрим полином m-го порядка

.

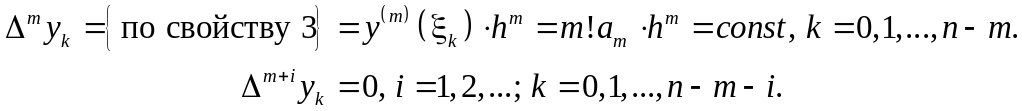
Таким образом для полинома -го порядка конечные разности -го порядка постоянны, а конечные разности порядков, больших, чем , равны нулю.

Пример 10. Пусть .

Рассмотрим сетку узлов Составить таблицу конечных разностей.

Заметим, что вторые разности постоянны в соответствии со свойством 4. Кроме того, верхняя строка таблицы относится к конечным разностям в точке x₀.

Замечание. Справедливо и обратное к свойству 4 утверждение: если для некоторой функции m-ные конечные разности постоянны при любом выборе шага, то это означает, что .

1.6 Интерполяционный полином Ньютона

Пусть - сетка равноотстоящих узлов. Известны табличные значения некоторой функции .

Запишем многочлен Лагранжа в следующем виде:

.

(16)

Введем безразмерную переменную

, для

где h – шаг. Очевидно, что для . Кроме того, для данной сетки

;

.

(17)

Потребуем выполнения условий совпадения значений полинома с табличными значениями в узловых точках

Далее по индукции получаем общую формулу для коэффициента

Заметим, что из определения q следует, что

Подставляя (17) и формулу для в (16), получаем:

(18)

Формула (18) называется первой интерполяционной формулой Ньютона или формулой «интерполирования вперед».

Замечание. Мы получили два различных представления для одного и того же интерполяционного полинома (интерполяционный полином Лагранжа и интерполяционный полином Ньютона). Отметим некоторые очевидные особенности практического применения этих двух видов.

Интерполяционный полином в форме Лагранжа содержит значения в явном виде. Это удобно, когда надо построить интерполяционный полином по той же сетке, но для другой функции . В этом случае достаточно значения поменять на .

Интерполяционный полином в форме Ньютона (18) содержит значения неявно (через конечные разности). Однако он удобен, когда для той же функции необходимо увеличить число узлов n для повышения точности. В этом случае к исходной записи многочлена достаточно добавить несколько таких же членов, если в запасе остались неиспользованными узлы сетки.

Кроме того, на практике обычно формулу (18) используют для интерполяции в точках x, близких к точке x₀. В этом случае q мало и требуется небольшое число членов ряда для достижения нужной точности.

В то же время многочлен в форме Лагранжа дает, как правило, наибольшую максимальную абсолютную погрешность в точках, близких к краям отрезка .

Приведем простейшие частые случаи интерполяции по Ньютону:

1) Линейная интерполяция, :

.

2) Квадратичная интерполяция, :

.

Пример 11. Задана таблица интерполяции в равноотстоящих узлах.

Используя интерполяцию по Ньютону, вычислить приближенно значение .

Составляем конечные разности и дополняем таблицу столбцами конечных разностей и . Обнаруживаем, что вторые конечные разности постоянны. Следовательно, и достаточно ограничиться многочленом 2-го порядка:

.

Используя первую строку таблицы и значение , получаем

.

Погрешность интерполяционной формулы Ньютона.

Нам известна теоретическая оценка абсолютнойпогрешности интерполяции в точке по Лагранжу

(5)

.

Преобразуем многочлен для случая равноотстоящих узлов:

Поскольку согласно формуле (17), , то

.

Т.о. для оценки погрешности в точке получаем:

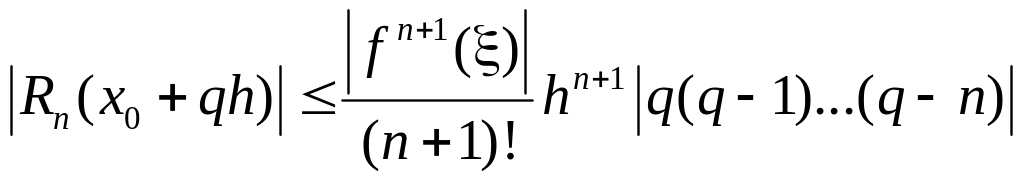
или

,

(19)

где

.

Из формулы (19) следует оценка для максимальной абсолютной погрешности интерполяционной формулы Ньютона на всем отрезке

.

(20)

Пример 12. Показать, что из формулы (20) следует более простая, но завышенная оценка

,

(21)

подчеркивающая степенную зависимость точности интерполяции от шага h.

Для вывода (21) показать сначала, что

.

Доказательство провести по индукции: и т.д.

Пример 13. Каков должен быть шаг h таблицы интерполяции для функции , чтобы при квадратичной интерполяции на отрезке абсолютная погрешность не превосходила ?

Ответ: . Использовать оценку (21).

Пример 14. Вывести вторую интерполяционную формулу Ньютона (формулу «интерполирования назад»).

Ищем интерполяционный многочлен в виде:

.

(22)

Накладывая условия

;

аналогично выводу формулы (18), получим общее выражение для :

Вводя безразмерную переменную

и преобразуя (22), получаем выражение для второй формулы Ньютона:

.

(23)

Для погрешности интерполяции получаем соответственно:

В формуле (23) используются конечные разности которые образуются в последних строках таблицы.

Замечание. Множество различных видов интерполяционных полиномов не исчерпывается приведенными тремя видами. Результат зависит от двух факторов: от вида сетки (равномерная или неравномерная) и от выбора базового узла . Например для равномерной сетки и при выборе базового узла в центральной части отрезка используются так называемые центральные разности. В результате получаются еще 3 вида записи интерполяционных полиномов: формулы Гаусса, Стирлинга и Бесселя [1].