1.2 Распространение ошибок округления в арифметических операциях.

1) Операции сложения и вычитания.

Пусть , . Тогда , где .

Поскольку , то ,

т.е. при сложении чисел предельные абсолютные ошибки складываются.

Не трудно убедиться, что такое же правило справедливо и для разности.

Вывевсти формулу для максимальной относительной погрешности разности ◄ самостоятельно ►.

2) Операция умножения.

Пусть ,

где , тогда

,

Следовательно,

,

т.е. .

Если последнее слагаемое имеет второй порядок малости по сравнению с первыми двумя, то им можно пренебречь. В этом случае получаем более простое правило: при умножении относительные максимальные ошибки приближенно складываются.

3) Операция деления.

Пусть , , .

Пример 4. Показать, что справедливо следующее правило:

.

Самостоятельно .

4) Погрешность вычисления функции при неточном задании аргументов.

Рассмотрим для определенности функцию двух переменных , непрерывно-дифференцируемую в области G R². Пусть приближенное значение точки , причем замкнутый прямоугольник

содержит обе указанные точки.

Пусть , , , .

По формуле конечных приращений Лагранжа имеем:

,

где - некоторая точка замкнутого прямоугольника .

Отсюда, оценивая обе части равенства по модулю, получим

.

Если известны оценки: , , где ( , то максимальная абсолютная ошибка вычисления функции:

.

1.3 Понятие близости в метрическом пространстве.

Определение 1. Множество X элементов произвольной природы (не обязательно числовое множество) называется метрическим пространством, если любой паре элементов поставлено в соответствие число , (метрика, или расстояние) в соответствии с аксиомами:

А1. тогда и только тогда, когда x=y.

А2. .

А3. – неравенство треугольника.

Определение 2. Говорят, что последовательность элементов метрического пространства X сходится к элементу , если .

Определение 3. Последовательность элементов метрического пространства X называется фундаментальной, если .

Определение 4. Метрическое пространство X называется полным, если любая фундаментальная последовательность его элементов сходится к некоторому элементу этого пространства.

Замечания.

Не любое метрическое пространство является полным.

Например, множество всех рациональных чисел с метрикой

не является полным, т.к., скажем, последовательность - фундаментальная, но - иррациональное число.

Сходимость большинства итерационных процессов удается доказать только в полном метрическом пространстве, следовательно, полнота играет важную роль в числовом анализе.

Определение 5. Множество X называется нормированным линейным пространством, если

оно является линейным пространством, т.е. в нем определены операции сложения элементов и умножения элемента на число с известными свойствами.

Любому элементу поставлено в соответствие число (норма x), удовлетворяющее аксиомам:

А1. ,

А2.

А3. – неравенство треугольника.

Замечание. Любое нормированное линейное пространство X можно считать метрическим, если ввести метрику по формуле

, (1)

Если последовательность нормированного пространства X сходится в смысле метрики (1), то говорят о сходимости по норме пространства X.

Нетрудно убедиться, что для метрики (1) выполняются все аксиомы метрики.

Приведем некоторые примеры классов функций и соответствующих линейных пространств.

Пример 5. Множество всех функций, заданных на отрезке [a,b] и имеющих на нем непрерывные производные до k -го порядка включительно, называется классом .

Пример 6. При k=0 получаем класс - множество непрерывных на отрезке [a,b] функций.

Если на ввести норму по формуле

,

(2)

то получим линейное нормированное пространство C[a,b] (операции сложения и умножения на число вводятся обычным образом f+g=f(x)+g(x), ).

Аксиомы А1, А2 – очевидно, выполняются. В справедливости А3 нетрудно также убедиться с помощью свойств модуля и теоремы Вейерштрасса.

Замечания.

Норму в классе можно ввести не единственным образом.

Например,

.

Сходимость последовательности по норме (2) – это равномерная сходимость:

.

Пространство C[a,b] с нормой (2) является полным в силу теоремы мат. анализа: равномерно сходящаяся последовательность в замкнутой области сходится к непрерывной функции.

Пример 7. Множество всех функций, p-я степень модуля которых интегрируема на отрезке [a,b], называется линейным нормированным пространством , если на нем введена норма по формуле

.

(3)

Сходимость по норме (3) называется сходимостью в среднем (при p=2 - среднеквадратичная сходимость).

Замечание. Пусть , тогда .

, .

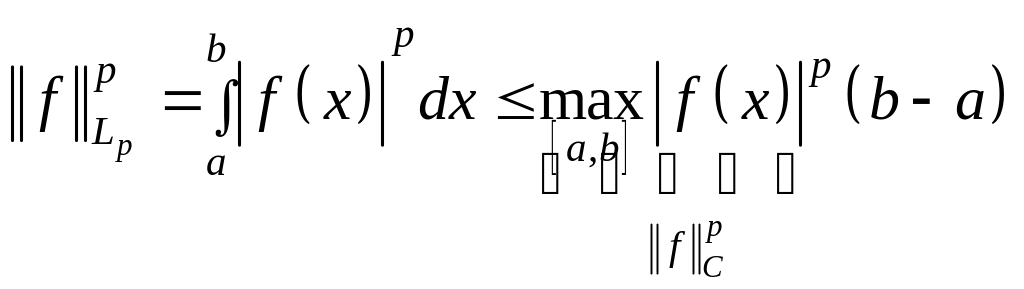Отсюда следует, что из сходимости последовательности по норме C следует ее сходимость по норме , но не наоборот.
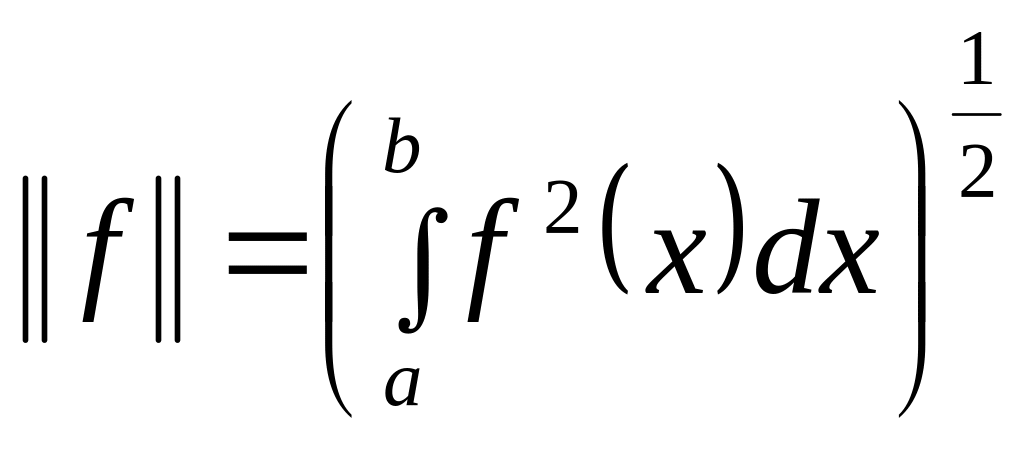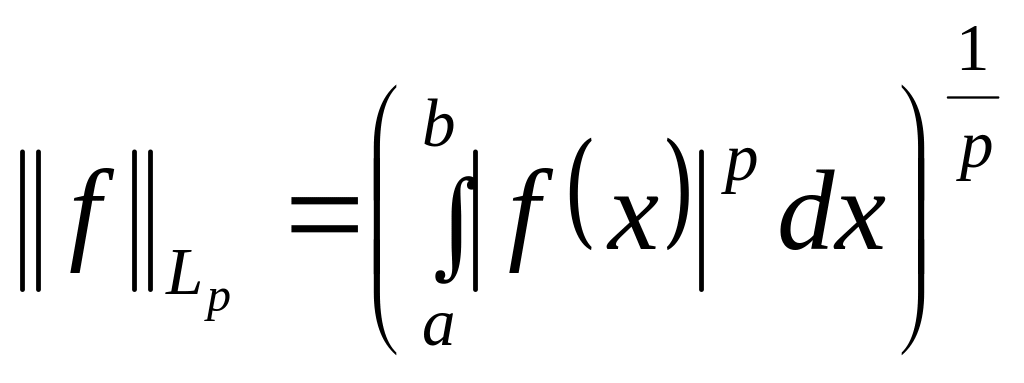