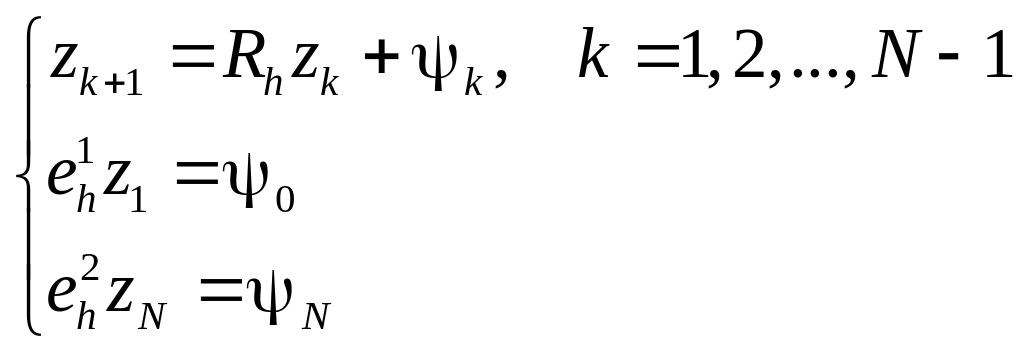4.4.3. Аппроксимация, устойчивость и сходимость разностных схем.

Пусть

(26)

Апроксимируем (26) на сетке с шагом . Тогда

(27)

Определение 1. Говорят, что задача (27) апроксимирует задачу (26) на сетке с порядком относительно шага , если выполняется условие:

,

где константа не зависит от . Заметим, что по определению сеточного решения . С другой стороны,

,

т.к. при подстановке точного решения в левую часть сеточного уравнения системы (27), получим несколько иную сеточную правую часть. Поэтому, обозначив

- - “невязка”, получаем:

-

- по условию аппроксимации порядка p.

Итак

(28)

Определение 2. Пусть

(29)

невозмущенная задача на сетке,

-

- возмущенная задача..

Разностная схема (29) устойчива по правой части, если малое изменение “правой части” ( ) приводит к малому изменению решения, т.е. если

где с₂ не зависит от h.

Пример 2. Пусть в задаче Коши функция f(x,u) линейна по переменным.

.

Привести к каноническому виду одношаговый итерационный процесс.

После аппроксимации производной на сетке w_h в точке (x_n,y_n), получаем

(30)

К такому же виду может быть приведена система уравнений в задаче Коши, где уже y_n – вектор, R_h – матрица.

Пример 3. Привести к каноническому виду краевую задачу (25) с граничными условиями первого рода.

Введем векторы:

и матрицу 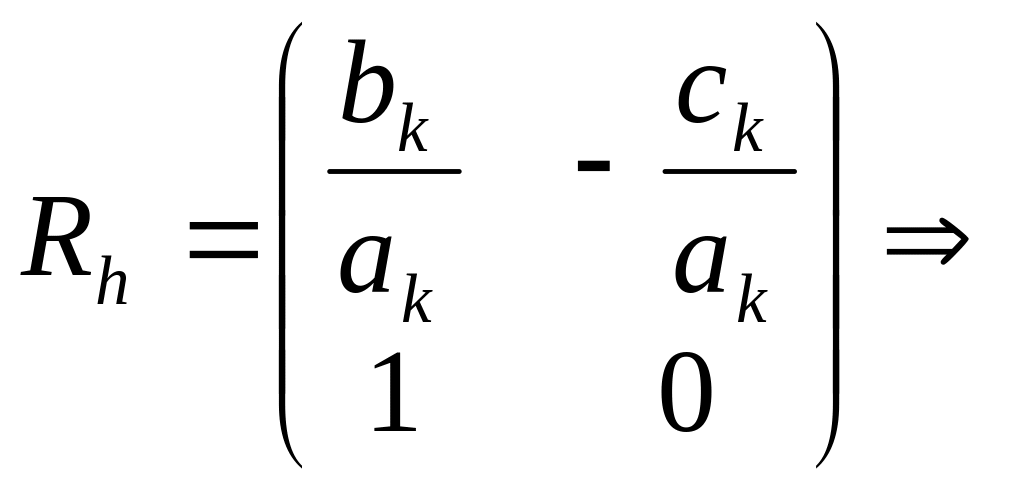(25) переписывается в виде

(31)

При таком преобразовании можно исследовать отдельно устойчивость по правой части и устойчивость по граничным условиям.

Теорема 4.5. (Необходимый и достаточный признак устойчивости процедуры (31) по правой части). Итерационная процедура устойчива по правой части тогда и только тогда, когда выполняется условие

, Где с не зависит от h (т.Е. От n). Без доказательства (см.[1,2]).

Однако это условие не всегда легко проверить. Поэтому для конкретных итерационных схем вырабатываются и доказываются более простые достаточные условия. Таковы, например, условия “диагонального преобладания” для схем прогонки.

Теорема 4.6. (Необходимый спектральный признак устойчивости). Пусть - собственные числа оператора R_h. Для устойчивости схемы (31) по правой части необходимо выполнение условия:

,

(32)

причем константа не зависит от h (от N).

Пусть (32) не выполняется для некоторого собственного значения . То есть, не существует такой константы , для которой (32) выполнялось бы для данного ₁. Фактически, это означает, что вместо линейного ограничения имеем:

, где 0<<1, c₁ - некоторая константа.

Пусть - соответствующий собственный вектор, т.е.

Оценим по сеточной норме:

.

Из последнего неравенства следует:

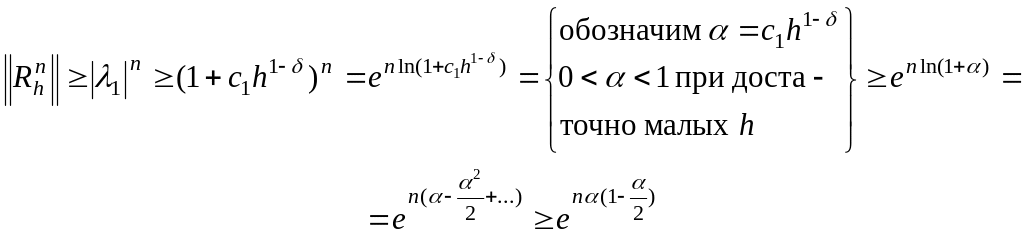
Заметим, что по условию на , поэтому

т.е. нарушается условие устойчивости, сформулированное ранее. Происходит экспоненциальный рост ошибки.

Рассмотрим снова сеточное уравнение вида (31)

Теорема 4.7. Пусть конечно-разностная задача (31) однозначно разрешима, аппроксимирует исходную дифференциальную задачу с порядком p относительно h и устойчива. Тогда имеет место сходимость в сеточной норме:

,

где - решение сформулированной разностной задачи; - точное решение дифференциальной задачи, взятое на сетке. При этом, если выполняется условие

,

то говорят, что имеет место сходимость порядка p.

Согласно условию теоремы имеет место аппроксимация порядка p:

	(33)
	(34)

где - невязка, которая получается при подстановке точного решения в левую часть уравнения. Подставляя в (33), получаем:

.

(10) (35)

В возмущенном уравнении

выберем в качестве возмущения невязку, т.е. положим

,

тогда

.

(11) (36)

В силу определения устойчивости по правой части имеем:

.

(12) (37)

Уравнения (33) и (37) имеют одинаковые правые части. В силу однозначной разрешимости задачи (31), имеем:

.

Подставим в (37)

.

Таким образом, мы одновременно доказали сходимость и установили, что порядок сходимости совпадает с порядком аппроксимации.