4.3.2. Метод Эйлера и его модификации.

Будем искать решение задачи (6) в прямоугольнике

.

Введем равномерную сетку на оси

, , .

Простейший итерационный процесс решения задачи (6) получается, если аппроксимировать производную на сетке правой конечной разностью. Обозначая приближенное решение на сетке , получим

или

(10) (10)

И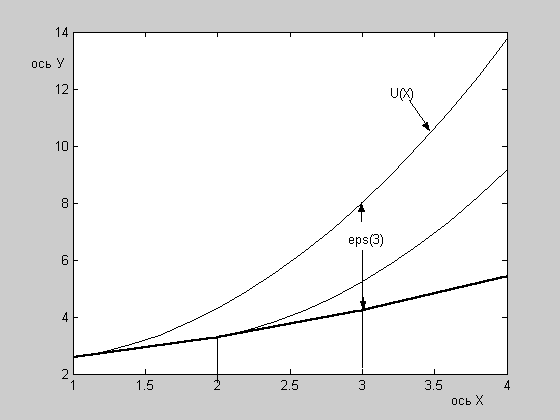 терационная процедура (10) представляет собой метод Эйлера (или метод ломаных). Графическая иллюстрация метода приведена на рис. 4.1

Рис. 4.1. Графическая иллюстрация метода Эйлера (метод ломаных). Жирная кривая – ломаная Эйлера;

U(x) – интегральная кривая, проходящая через начальную точку (1, U(1));

шаг сетки h = 1. eps(3) – погрешность в точке x₂ = 3.

Начав движение из точки на точном решении , итерационное решение образует ломаную линию, каждый отрезок которой представляет собой касательную к кривой , проходящую через данную точку.

Действительно, запишем уравнение касательной к u(x) в точке и положим :

.

Далее, аналогичным образом, строим касательную в точке и положим

и т.д.

Здесь – та интегральная кривая, которая проходит через точку (x₁,y₁).

Из рисунка видно, что ошибка растет с номером k. Выясним, каков порядок этой ошибки в сеточной норме

.

Будем считать, что ошибка округления имеет порядок не меньший, чем . Тогда из (10) следует:

(11)

Разложим точное решение в точке с такой же точностью:

(12)

Вычтем(12) из (11) 

(13)

где .

В силу условий теоремы существования и единственности частные производные ограничены в прямоугольнике : .

Обозначим и оценим (13) по модулю

по условию.

Обозначим

(10) (14)

Теорема 4.4. Для метода Эйлера имеет место следующая оценка погрешности:

(11) (15)

Из (14) следует (используем рекурсию «назад»):

Используя алгебраическое тождество

Получаем:

(12)

В последнем неравенстве использован второй замечательный предел.

Учитывая, что

получаем

,

т.е. оценку (15).

Замечание. Из соотношений (14) и (15) следует, что

1. Ошибка растет с номером шага k.

2. Порядок ошибки в методе Эйлера .

Рассмотрим несколько модификаций метода Эйлера повышенной точности.

Метод предиктор-корректор. Проинтегрируем обе части уравнения (6) по отрезку на равномерной сетке :

.

Левую часть полученного уравнения вычисляем по формуле Лейбница:

.

Для вычисления правой части используем квадратурную формулу трапеций:

где погрешность, определяемая формулой

.

Если отбросить остаточный член, то получаем неявную итерационную схему.

(13) (16)

Аналогично тому, как оценивается ошибка в методе Эйлера, можно показать, что результирующая ошибка метода (16) имеет порядок (теряется один порядок при приближении к концу отрезка).

Т.к. схема (16) неявная, то ее следует решать методом итераций для фиксированных точек и . Более простой путь заключается в следующем. Используем в (16) только 2 последовательных этапа итераций:

(14) (17)

с начальным условием: .

Полученная схема (17) имеет также порядок точности и носит название «метод предиктор-корректор» .

Поясним геометрический смысл названия.

На первом этапе предсказывается значение по методу Эйлера. На втором этапе это значение корректируется путем усреднения угловых коэффицинтов в точках и . За счет коррекции точность метода и повышается на порядок по сравнению с методом Эйлера.

Метод средней точки. Найдем сначала значение в промежуточной точке отрезка по простому методу Эйлера.:

- обозначим так найденное значение на половинном шаге от точки . Затем в полученной точке вычислим угловой коэффициент касательной и в этом направлении совершим движение из точки в точку :

.

Полученный метод имеет 2-ой порядок точности и называется модифицированным методом Эйлера с коррекцией углового коэффициента на половинном шаге или более коротко─метод средней точки.

Существует общий теоретический подход к построению явных итерационных методов решения задачи Коши повышенного порядка точности . Это так называемые Методы Рунге-Кутты -го порядка, удовлетворяющие следующим условиям.

1. Это одношаговые методы, т.е. при переходе из точки в точку используется лишь информация о предыдущей точке .

2. Процедура согласуется с рядом Тейлора вплоть до членов порядка , где - порядок метода.

3. Метод не использует производных от , а требует только вычисления функции в различных точках сетки, причем число вычислений функции - минимально возможное для данного порядка.

Заметим, что метод Эйлера является частным случаем метода Рунге-Кутты, имеющий наименьший первый порядок точности, а методы средней точки и предиктор-клрректор - методы Рунге-Кутты второго порядка.

Остановимся вкратце на средствах пакета MATLAB решения задачи Коши. Здесь реализованы следующие процедуры Рунге-Кутты:

ode23 – метод второго и третьего порядка;

ode45 - метод четвертого и пятого порядка;

ode113 – многошаговый метод Адамса переменного порядка;

При практическом применении методов повышенной точности возникает вопрос, какой формулой пользоваться на практике? Если априори известно, что - достаточно гладкая функция, например, , то наиболее эффективна процедура ode45 или ode113. Если же гладкость функции недостаточна, то лучше использовать методы второго и третьего порядка. В лабораторной работе 7 предусмотрено знакомство с этими командами.