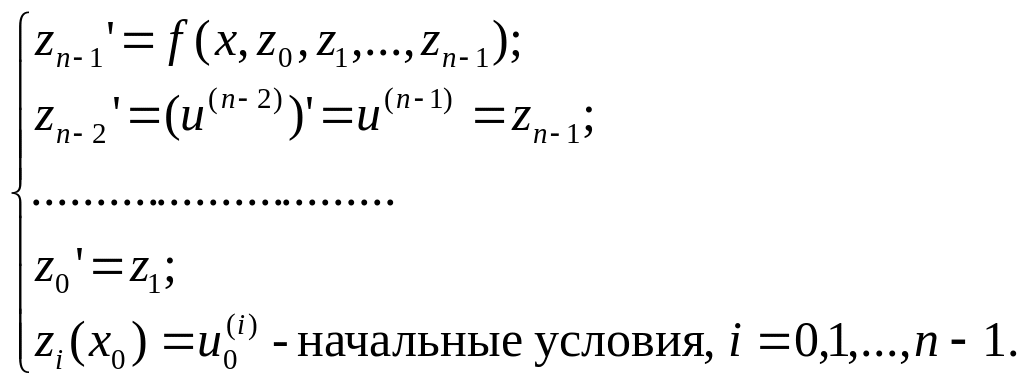- •Содержание
- •Глава 1. Численные методы в теории приближений
- •Глава 2. Численное интегрирование.
- •Глава 3. Численные методы алгебры.
- •Глава 4. Численные методы решения обыкновенных дифференциальных уравнений.
- •Предисловие
- •Глава 1. Численные методы в теории приближений.
- •1.1. Структура погрешности в численном анализе.
- •1.2 Распространение ошибок округления в арифметических операциях.
- •1.3 Понятие близости в метрическом пространстве.
- •1.4. Задача интерполяции как простейшая задача приближения функций.
- •1.5 Конечные разности и их свойства.
- •1.6 Интерполяционный полином Ньютона
- •1.7 Многочлены Чебышева, их свойства и применение в задаче интерполяции.
- •1.7.1. Основные определения.
- •1.7.2. Простейшие свойства многочленов Чебышева.
- •1.7.3. Применение многочленов Чебышева в задаче интерполяции.
- •1.8 Среднеквадратичное приближение функций.
- •1.8.1. Общая постановка задачи и ее разрешимость.
- •1.8.2. Среднеквадратичное приближение функций алгебраическими многочленами.
- •1.8.3. Среднеквадратичная ошибка аппроксимации полиномами Лежандра.
- •Глава 2. Численное интегрирование.
- •2.1. Использование функциональных рядов.
- •2.2. Квадратурные формулы на основе интерполяции.
- •2.3. Квадратурные формулы Ньютона-Котеса.
- •2.4. Некоторые общие свойства ортогональных с весом полиномов.
- •2.5.Квадратурные формулы Гаусса-Кристоффеля.
- •Глава 3. Численные методы алгебры.
- •3.1. Принцип сжатых отображений.
- •3.2. Метод простых итераций для функциональных уравнений.
- •3.3. Метод Ньютона.
- •3.4. Численные методы решения систем лау.
- •3.4.1. Прямые методы решения систем лау.
- •3.4.2. Нормы векторов и матриц.
- •3.4.3. Обусловленность матриц и систем уравнений.
- •3.4.4. Итерационные методы решения систем лау.
- •3.4.5. Стационарные итерационные процедуры.
- •Глава 4. Численные методы решения обыкновенных дифференциальных уравнений (оду).
- •4.1. Численное дифференцирование на основе интерполяции.
- •4.2. Численное дифференцирование на равномерной сетке.
- •4.3. Задача Коши для оду.
- •4.3.1. Постановка задачи.
- •4.3.2. Метод Эйлера и его модификации.
- •4.4. Численные методы решения краевых задач для оду.
- •4.4.1. Постановка задачи для диффернциального уравнения 2-го порядка.
- •4.4.2. Метод конечных разностей (метод сеток).
- •4.4.3. Аппроксимация, устойчивость и сходимость разностных схем.
- •, Где с не зависит от h (т.Е. От n). Без доказательства (см.[1,2]).
- •Литература
Глава 4. Численные методы решения обыкновенных дифференциальных уравнений (оду).
4.1. Численное дифференцирование на основе интерполяции.
Если функция
![]() задана таблично, то аналитическое
дифференцирование невозможно. Строится
интерполяционный полином и его производную
принимают приближенно за
задана таблично, то аналитическое
дифференцирование невозможно. Строится
интерполяционный полином и его производную
принимают приближенно за
![]() .
.
Запишем 1-ую форму интерполяционного полинома Ньютона на равномерной сетке:
|
(1) |
где
![]()
![]() .
.
![]() - погрешность
интерполяции.
- погрешность
интерполяции.
Дифференцируя (1), получим:
![]() ,
,
где
![]() -
-
- формула теоретической
погрешности производной в точке
![]() .
.
Пример 1.
Пусть
![]() .
Вычислить приближенно первую производную
.
Вычислить приближенно первую производную
![]() и оценить погрешность (теоретическую).
и оценить погрешность (теоретическую).
На данной сетке
получаем:
![]() .
.
Интерполяционный полином третьего порядка имеет вид:
![]() ;
;
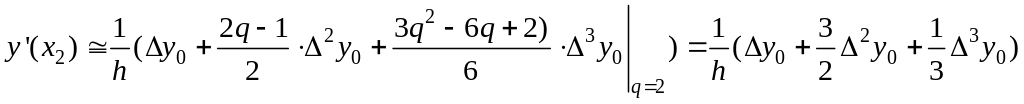 ;
;
![]() .
.
4.2. Численное дифференцирование на равномерной сетке.
Пусть задана сетка
![]() .
.
Теорема 4.1.
Обозначим
![]() и т.д. и пусть
и т.д. и пусть
![]() ,
тогда существует такая точка
,
тогда существует такая точка
![]() ,
для которой справедлива формула:
,
для которой справедлива формула:
|
(2) |
Т.к.
,
то справедливо разложение Тейлора с
центром в точке
![]() и остаточным членом в форме Лагранжа:
и остаточным членом в форме Лагранжа:
![]() .
.
В точке
![]() получаем:
получаем:
![]() ,
,
откуда следует
![]() ,
,
что и требовалось доказать.
Теорема 4.2. Пусть
![]() тогда
тогда
|
(3) |
Самостоятельно. См. ход доказательства следующей теоремы .
Теорема 4.3. Пусть
![]() ,
тогда существует такая точка
,
тогда существует такая точка
![]() ,
что справедлива формула
,
что справедлива формула
|
(4) |
По условию теоремы справедливо тейлоровское разложение функции с центром в точке :
![]() ,
(5)
,
(5)
где
![]() .
Положим в формуле (5) последовательно
.
Положим в формуле (5) последовательно
![]() и
и
![]() :
:
![]()
Складывая эти две формулы, получим
![]() .
.
В силу непрерывности
четвертой производной
![]() :
:
![]() ,
,
Откуда следует:
![]() ,
т.е. формула (4)
.
,
т.е. формула (4)
.
Замечание. Формулы
(2), (3) и (4) называются формулами
численного дифференцирования.
При этом формула (2) аппроксимирует
первую производную в узле
правой
конечной разностью
и имеет порядок
точности
![]() (т.е.
первый
порядок);
(т.е.
первый
порядок);
формула (3)
аппроксимирует первую производную
центральной конечной разностью и имеет
порядок
точности
![]() (второй
порядок);
(второй
порядок);
формула (4) аппроксимирует вторую производную в узле центральной конечной разностью и имеет порядок точности (второй порядок).
4.3. Задача Коши для оду.
4.3.1. Постановка задачи.
Задача Коши для ОДУ первого порядка для функции одной переменной ставится следующим образом:
|
(6) |
Более общая постановка задачи Коши для дифференциального уравнения n-го порядка:
|
(7) |
Здесь
![]() - заданные числа (начальные условия).
- заданные числа (начальные условия).
Задача (7) с помощью замены переменных
![]() ,
,
![]()
сводится к системе дифференциальных уравнений первого порядка:
|
(8) |
Систему (8) можно переписать в векторном виде:
|
(9) |
где
![]() ,
,
![]() ,
,
![]() .
.
Система (9) исследуется и решается аналогично одномерной задаче Коши (6), поэтому важно изучить, прежде всего, численные методы решения задачи (6).
В курсе математического
анализа формулируется и доказывается
теорема существования и единственности
решения задачи Коши. Отметим, что для
выполнения теоремы необходимо и
достаточно, чтобы функция
![]() имела непрерывные частные производные
по
имела непрерывные частные производные
по
![]() в замкнутой ограниченной области
в замкнутой ограниченной области
![]() на плоскости
на плоскости
![]() .
.